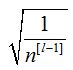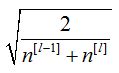【deeplearning.ai】第二门课:提升深层神经网络——权重初始化
一、初始化
合理的权重初始化可以防止梯度爆炸和消失。对于ReLu激活函数,权重可初始化为:
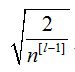
也叫作“He初始化”。对于tanh激活函数,权重初始化为:
也称为“Xavier初始化”。也可以使用下面这个公式进行初始化:
上述公式中的l指当前处在神经网络的第几层,l-1为上一层。
二、编程作业
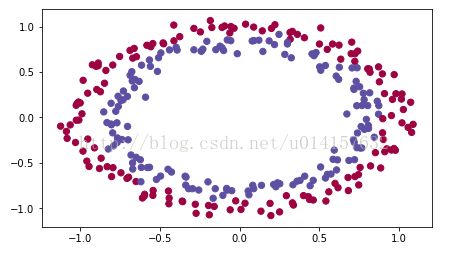
有如下二维数据:
训练网络正确分类红点和蓝点。导入需要的扩展包,其中init_utils.py在这里下载
import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
from init_utils import sigmoid, relu, compute_loss, forward_propagation, backward_propagation
from init_utils import update_parameters, predict, load_dataset, plot_decision_boundary, predict_dec
%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# load image dataset: blue/red dots in circles
train_X, train_Y, test_X, test_Y = load_dataset()1、建立神经网络模型
def model(X, Y, learning_rate = 0.01, num_iterations = 15000, print_cost = True, initialization = "he"):
"""
Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID.
Arguments:
X -- input data, of shape (2, number of examples)
Y -- true "label" vector (containing 0 for red dots; 1 for blue dots), of shape (1, number of examples)
learning_rate -- learning rate for gradient descent
num_iterations -- number of iterations to run gradient descent
print_cost -- if True, print the cost every 1000 iterations
initialization -- flag to choose which initialization to use ("zeros","random" or "he")
Returns:
parameters -- parameters learnt by the model
"""
grads = {}
costs = [] # to keep track of the loss
m = X.shape[1] # number of examples
layers_dims = [X.shape[0], 10, 5, 1]
# Initialize parameters dictionary.
if initialization == "zeros":
parameters = initialize_parameters_zeros(layers_dims)
elif initialization == "random":
parameters = initialize_parameters_random(layers_dims)
elif initialization == "he":
parameters = initialize_parameters_he(layers_dims)
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.
a3, cache = forward_propagation(X, parameters)
# Loss
cost = compute_loss(a3, Y)
# Backward propagation.
grads = backward_propagation(X, Y, cache)
# Update parameters.
parameters = update_parameters(parameters, grads, learning_rate)
# Print the loss every 1000 iterations
if print_cost and i % 1000 == 0:
print("Cost after iteration {}: {}".format(i, cost))
costs.append(cost)
# plot the loss
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters2、将权重初始化为0
def initialize_parameters_zeros(layers_dims):
"""
Arguments:
layer_dims -- python array (list) containing the size of each layer.
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
b1 -- bias vector of shape (layers_dims[1], 1)
...
WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
bL -- bias vector of shape (layers_dims[L], 1)
"""
parameters = {}
L = len(layers_dims) # number of layers in the network
for l in range(1, L):
parameters['W' + str(l)] = np.zeros((layers_dims[l], layers_dims[l-1]))
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
return parameters训练网络:
parameters = model(train_X, train_Y, initialization = "zeros")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)训练完成后绘制的cost曲线:
训练准确率为0.5,测试准确率为0.5,。将测试集的预测结果输出:
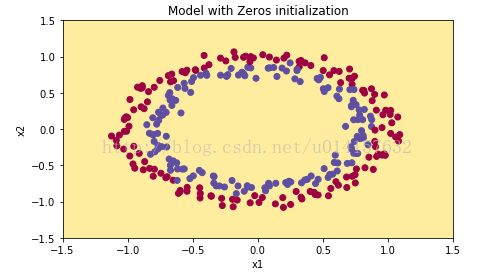
画出分类界线:
这个模型将所有测试集都预测成了0,将权重初始化为0使网络没有打破平衡,每个神经元都学到了相同的东西。
3、将权重随机初始化为较大的数
def initialize_parameters_random(layers_dims):
"""
Arguments:
layer_dims -- python array (list) containing the size of each layer.
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
b1 -- bias vector of shape (layers_dims[1], 1)
...
WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
bL -- bias vector of shape (layers_dims[L], 1)
"""
np.random.seed(3) # This seed makes sure your "random" numbers will be the as ours
parameters = {}
L = len(layers_dims) # integer representing the number of layers
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1])*10
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
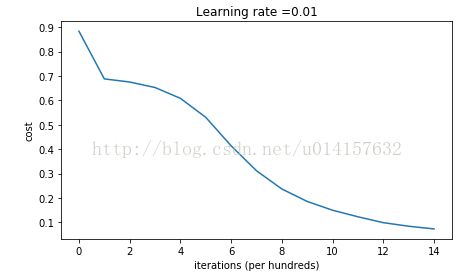
return parameters训练这个模型,得到cost曲线:
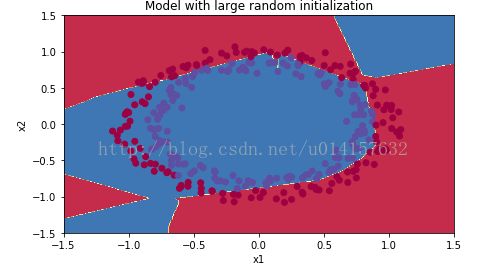
训练集准确率为0.83,测试集准确率为0.86。分类界线如下:
可以看出cost一开始很大,是因为权重初始化得较大,使某些样本的输出(sigmoid激活函数)非常接近0或1。糟糕的初始化可能导致梯度爆炸或消失,同时降低训练速度。
4、使用He初始化
def initialize_parameters_he(layers_dims):
"""
Arguments:
layer_dims -- python array (list) containing the size of each layer.
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
b1 -- bias vector of shape (layers_dims[1], 1)
...
WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
bL -- bias vector of shape (layers_dims[L], 1)
"""
np.random.seed(3)
parameters = {}
L = len(layers_dims) - 1 # integer representing the number of layers
for l in range(1, L + 1):
parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1]) * np.sqrt(2/layers_dims[l-1])
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
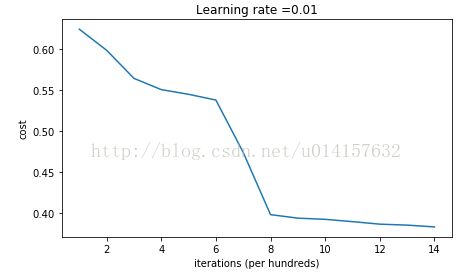
return parameterscost曲线:
训练集的准确率为0.9933333,测试集的准确率为0.96。分类界线: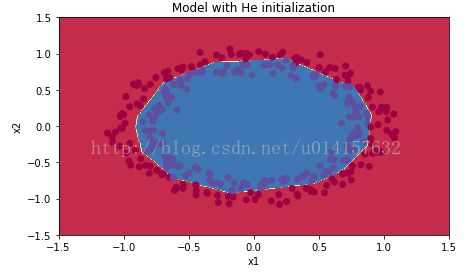
可以看出合理的权重初始化使网络性能得到了很好的改善。