PRML第三章笔记

这是关于PRML第三章的学习笔记。主要从内容思想的理解，具体的理论推导需要结合原文以及概率论的知识。这一章主要讲述线性回归，解释了下面主要问题：

1.线性基函数模型中过拟合问题处理方式；
2.如何分别从频率角度和贝叶斯角度理解模型复杂度问题？
3.贝叶斯线性回归的顺序性质怎么直观地理解（里面有一副图非常直观）？
4. 在贝叶斯方法中，如何评估模型证据，以及回归参数w的有效性（是否有效、有效个数）？特别地，对于拟合参数的不同维度，什么时候靠近训练数据集的最大似然估计，什么时候更加倾向于最初的先验假设（也就训练数据集对该参数的作用有限）？

主要讲述两个方向：
第一、频率角度的回归模型，以及通过损失函数比较模型，通过加入正则项防止过拟合
第二、贝叶斯角度的回归模型，以及通过模型证据比较模型，贝叶斯本身可以防止过拟合
（贝叶斯的模型证据是通过数据计算的，不用把数据集分开，留出验证集）

一、线性基函数模型：也就是把最常见的x的线性组合变成的基函数的线性组合:
（1）线性基函数模型介绍

这里的是基函数，可以是非线性的函数，代表非线性变换。在许多模式识别的实际应⽤中，我们会对原始的数据变量进⾏某种固定形式的预处理或者特征抽取。如果原始变量由向量x组成，那么特征可以⽤基函数{φj(x)}来表⽰。
（2）常见基函数形式

1，最大似然等价于最小平方损失 （L=LS）：在条件⾼斯噪声分布的情况下，线性模型的似然函数的最⼤化等价于平⽅和误差函数的最⼩化
（1）概率建模

在Gaussian 零均值情况下,Linear model从频率主义出发的MLE就是 Least square：

（2）求参数w,和beta的解（梯度等于0）
最小2乘的解就是广义逆矩阵乘输出值：

Gaussian的precision也可以计算出来：

2，几何理解
数据N个，基的维度M小于N ,y=(y1…yn).T,t=(t1,…tn).T ，而y=wTϕ(x)，所以y在ϕ所张成的空间里，均方误差最小实质上是t与y的距离最小，也就是当且仅当t垂直于ϕ所张成的平面的时候。也就是说y就是t在ϕ空间中的正交投影。
如果M>N时候，很可能导致矩阵ϕTϕ是奇异的（我猜的，待考虑），这时候ϕTϕ中元素值都很大，导致wML也很大，称之为degeneracies(退化)。

3，序列学习 or 在线学习：就是随机梯度下降的方法

4，正则化：
频率主义会导致 过拟和，加入正则,得到的最小2乘解：

正则参数对model结果的影响：

消除过拟和，正则的几何解释：

5，多输出
两种方案：
（1）输出视作互相独立的，那么对于每一个输出都有一套基
（2）所有的输出都使用相同的基，只是使用不同的w来计算。
（常用第二种情况）

二、偏置-方差分解
正则化需合适的λ ,第三章从两个角度解释这个问题，一个是频率派的角度，一个是贝叶斯派的角度。 两个学派的区别在于是否视概率参数是随机变量。（这里是用频率学思想来解决过拟合问题。即：平衡偏差和方差）

（1）平⽅损失函数：讨论回归问题的决策论时，我们考虑了不同的损失函数。⼀旦我们知道了条件概率分布p(t | x)，每⼀种损失函数都能够给出对应的最优预测结果。使⽤最多的⼀个选择是平⽅损失函数，此时最优的预测由条件期望（记作h(x)）给出，即：

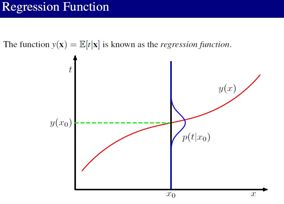
（2）损失函数的分解：


第二项与y(x)无关，即与w无关，仅仅与数据本身有关，因此不考虑；第一项为了使之最小，当然要使y(x)=h(x)，然而问题是数据量是有限的，必然导致y(x)无法完整的描述数据，也就是没法精确的求出回归函数h(x)，因此会存在一定的差。
贝叶斯观点认为，y(x)之所以无法精确的逼近h(x)是由于w是随机量而不是固定值，也就是说w本身就是不确定的。 而频率派是这样描述的，首先有一个无限大的数据集，我们每次只能选择其中一个样本来处理，因此一个样本导致一个w（对该数据集而言w本身是未知的常量），这才是y(x)无法等于h(x)的原因。 为了描述这种现象，使E(L)的第一项对所有的数据集积分：

学习到的模型和真实的模型的期望由2部分组成：
1–> Bias 2–> Variance。Bias表示的是学习到的模型和真实模型的偏离程度,Variance表示的是学习到的模型和它自己的期望的偏离程度。

（3）Variance小的情况下,Bias就大，Variance大的情况下,Bias就小，我们就要tradeoff它们。正则项在控制 Bias 和 Variance，使他们可以平衡：

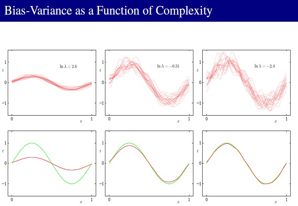
以上就是频率学派的观点。其最大的局限性在于确定合适的模型复杂度的问题。这个问题不能简单地通过最⼤化似然函数来确定，因为这总会产⽣过于复杂的模型和过拟合现象。独⽴的额外数据能够⽤来确定模型的复杂度，但是这需要较⼤的计算量，并且浪费了有价值的数据。

三、贝叶斯线性模型
1，参数分布：
（1）先验分布与后验分布
贝叶斯线性模型认为参数W是随机变量，先验分布是高斯分布，对应的后验分布也是高斯分布（具体推导见第二章）。

（2）贝叶斯如何控制模型复杂度：贝叶斯就是求后验概率最大化

后验分布关于w的最⼤化等价于对平⽅和误差函数加上⼀个⼆次正则项进⾏最⼩化。其中λ = α/β，所以他可以防止过拟合。

（3）顺序性质：如果数据点是顺序到达的，那么任何⼀个阶段的后验概率分布都可以看成后续数据点的先验。

数据产生：f=-0.3+0.5x，x在[-1,1]间均匀采样，然后叠加一个N(0，0.2)噪声。
模型：先验这里写图片描述 α=2
序列化过程：第一个数据t1,p(w∣t1)∝p(t1∣w)p(w)
来第二个数据，若整体考虑：
p(w∣t1，t2)∝p(t1,t2∣w)p(w)∝p(t2∣w)p(t1∣w)p(w)∝p(t2∣w)p(w∣t1)
可见如果我们把第一个数据后的后验概率视作为先验，那么新的后验概率就正比于“新的先验”和“新的似然概率”之积。
如图：（r=1, c=2）表示没有数据时先验概率的图；(1,3)表示数据空间中的六个线性模型，该模型参数w取样于（1,2）；（2,1）中‘+’表示真实的w值，考虑lnp(t|w)=A-B(t1−w0−w1x1)2这其实是这个公式的图，当(t1=w0+w1x1)显然就是最中间的那条直线；（2,2）中就是(1,2)*(2,1)的结果；（2,3）‘。’表示所观察的数据，可以看到新采样到的w保证了直线都在该数据周围。以下类推，当可观测数据越来越多的时候，模型就越来越精确。

2，预测分布
预测分布定义为：（定义，贝叶斯的参数是一个随机变量，所以预测值关于w求积分）

这里观察数据x永远作为条件，因此被忽略。注意到积分中的两个式子都是高斯，根据PRML式子(2.115)结果有：

（1,1）图中点作为数据计算w的后验概率得mN,SN,绿色直线代表原始sin曲线，红色区域间距代表预测值的方差，红色直线代表预测值的均值。

3，等价核：（这块儿主要是第六章的类容）
注意，由于后验分布是⾼斯分布，它的众数恰好与它的均值相同。因此最⼤后验权向量的结果就是w_MAP = m_N。


被称为平滑矩阵（smoother matrix）或者等价核（equivalent kernel）。像这样的回归函数，通过对训练集⾥⽬标值进⾏线性组合做预测，被称为线性平滑（linear smoother）

四、贝叶斯模型比较
（1）贝叶斯角度的模型选择，预测分布为平均各个模型
M：概率分布，由w决定
w：决定M的参数
（NOTE：w决定M，但p(w)!=p(M)）
D：观察到的数据，由于x不考虑其概率，可以认为就是指y
model evidence:p(D∣Mi),表示不同模型下数据产生的概率 贝叶斯的“不同模型”来源于P(Mi),简单起见可以假设所有的模型具有相同的先验概率。

（2）模型平均的简单近似就是找一个最可能的模型，即是模型证据最大的

（3）模型证据的认识
忽略掉Mi,并假设p(w)和p(w|D)如下图：

右式第一项表示给定最佳参数w_wap的log likelihood，在wap情况下其值较大，第二项表示最佳参数下的惩罚度，其值比较小，当然还取决于先验概率。
我们选择的模型当然要使证据p(D|M)越大越好，如果M比较大，第一项必然变大（模型拟合的更好），而第二项会变的很小，这就是一个trade-off。

五、证据近似
（1）证据近似的含义-一种计算最大化边缘似然函数的方法
在线性模型中，前面还有两个参数α,β（噪声方差参数和w的先验方差参数），在全bayes观点看来，其实应该视为随机变量，然后求预测值时应该对他们积分，但是这种方式是不可解析的。因此有一种近似的方法，就是通过最大化marginal likelihood function(对w积分去掉w)方法来求α,β的点估计。 全贝叶斯预测公式（预测分布）：

假设p(α,β∣t) 仅在α^,β^处非常尖锐，那么上式可以简化为：

那么现在的问题是如何求α^,β^

如果假设p(α,β)分布是平坦的，那么最大化后验概率就是最大化似然函数。这样参数的就能直接由训练数据给出。

（2）计算证据函数

（3）最大化证据函数

（4）参数的有效个数

这里考察γ这个量的意义。上图其实描述的是p(w),p(t∣w)这两个式子的图（NOTE:书里现在讲的evidence是指p(t∣w))。这里假设p(t∣w)仅有两个参数，假设λ1,2.
我们知道p(t∣w)是高斯形式，其协方差矩阵就是A，因此λi是对应的特征值。假设λi对应wi(这里已经将参数空间旋转使之与特征向量平行，所以这里的w可能和前面的w不太一样，但是个数是不变的)。如果λi>>α，那么λ/λ+α=1代表的意义是证据函数在wi这个方向变化变化较大，称之为well determined参数；反之λ/λ+α=0，意指证据函数在这个方向上变化较小，不需要这个特征，如图在u1方向上变化就较大而在u2上较小。再考察γ的表达式，其实就是统计well determined参数的个数，这就是γ的意义。
（NOTE:这个图感觉和书上实际举例有一点冲突，感觉应该将椭圆旋旋或者wap点在右下比较合理）
（NOTE:高斯协方差矩阵的特征向量正交？）
对参数beta的理解：
对比下面两个式子：

第一个式子是上节推导的结果的方差，第二个式子是最开始用ML直接推导的结果的方差。
两个相差一个γ。
首先解释一下自由度：是指当以样本的统计量来估计总体的参数时，样本中独立或能自由变化的数据的个数称为该统计量的自由度。
先看下面两个式子：

上面式子是方差有偏估计，下面是无偏的。注意到其实是因为样本均值的存在减少了1个自由数据的自由度导致的。（NOTE：书上说是因为拟合噪声导致的，不太好理解）
同理，由于在bayes估计中，发现有γ个有效参数，必然导致在估计方差时要降低γ个自由度。
（NOTE:假想数据t，x与w构成了N个方程，由于有效个数为γ，因此实际能用上的数据为γ个，所以自由变化的就是N-γ了）

现在仍然举第一章1.1节的例子，采用sin数据，M=10，假定β已经是优化值了
（NOTE:这里有两张图还要研究）

六、固定基函数的局限
前面的线性模型有很多优点，参数线性使得该模型有闭式解，而且bayes模型也是可解析的；能够通过基的选择解决大量非线性问题。但是存在以下两个缺点：
（1）基是固定的，而且在建模之前要选择好：比如多项式基选择很可能导致结果拟合的不好
（2）维数灾难：指随着数据维度升高，建模复杂度以指数形式增长。
比如：多项式基，数据维度为M时，若以3次建模，则需要O（M3），这里当然不是指数增长，但是仍然增长非常快，以至计算困难。
解决方案：降维
(1)数据x本身是高度相关的
(2)预测值y仅仅依赖于部分x