数据比赛大杀器----模型融合(stacking&blending)

参考文献链接

---

英文版本
http://mlwave.com/kaggle-ensembling-guide/
这里写链接内容

这个是上面英文翻译过来的汉语翻译版本
kaggle比赛集成指南
http://m.blog.csdn.net/article/details?id=53054686

---

搜狗比赛第五名的stacking思路
http://prozhuchen.com/2016/12/28/CCF%E5%A4%A7%E8%B5%9B%E6%90%9C%E7%8B%97%E7%94%A8%E6%88%B7%E7%94%BB%E5%83%8F%E6%80%BB%E7%BB%93/

---

kaggle官方博客 stacking融合
http://blog.kaggle.com/2016/12/27/a-kagglers-guide-to-model-stacking-in-practice/

汉语版翻译如下

Kaggler的“实践中模型堆叠指南”

---

---

介绍
堆叠（也称为元组合）是用于组合来自多个预测模型的信息以生成新模型的模型组合技术。通常，堆叠模型（也称为二级模型）因为它的平滑性和突出每个基本模型在其中执行得最好的能力，并且抹黑其执行不佳的每个基本模型，所以将优于每个单个模型。因此，当基本模型显著不同时，堆叠是最有效的。关于在实践中怎样的堆叠是最常用的，这里我提供一个简单的例子和指导。

本教程最初发布在Ben的博客GormAnalysis上。

https://github.com/ben519/MLPB/tree/master/Problems/Classify%20Dart%20Throwers

请随意借鉴本文中使用的来自机器学习问题参考书的相关代码和数据集。

---

另外的python 版本的blending

https://github.com/emanuele/kaggle_pbr

---

动机
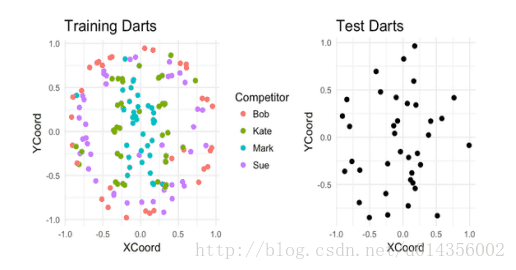
假设有四个人在板子上投了187个飞镖。对于其中的150个飞镖，我们可以看到每个是谁投掷的以及飞镖落在了哪。而其余的，我们只能看到飞镖落在了哪里。我们的任务就基于它们的着陆点来猜测谁投掷的每个未标记的飞镖。

---

K最近邻（基本模型1）
让我们使用K最近邻模型来尝试解决这个分类问题。为了选择K的最佳值，我们将使用5重交叉验证结合网格搜索，其中K =（1,2，… 30）。在伪代码中：
1.将训练数据分成五个大小相等的数据集。调用这些交叉测试。
2.对于K = 1,2，… 10
1.对于每个交叉测试
1.组合其他四个交叉用作训练交叉
2.在训练交叉上使用K最近邻模型（使用K的当前值）
3.对交叉测试进行预测，并测量所得预测的准确率
2.从五个交叉测试预测中计算平均准确率
3.保持K值具有最好的平均CV准确率
使用我们的虚构数据，我们发现K = 1具有最佳的CV性能（67％的准确性）。使用K = 1，我们现在训练整个训练数据集的模型，并对测试数据集进行预测。 最终，这将给我们约70％的分类精度。

支持向量机（基本型2）
现在让我们再次使用支持向量机解决这个问题。此外，我们将添加一个DistFromCenter功能，用于测量每个点距板中心的距离，以帮助使数据线性可分。 使用R的LiblineaR包，我们得到两个超参数来调优：
类型
1.L2-正则化L2丢失支持向量分类（双重）
2.L2正则化L2丢失支持向量分类（原始）
3.L2-正则化L1损失支持向量分类（双重）
4.Crammer和Singer的支持向量分类
5.L1正则化L2丢失支持向量分类
成本
正则化常数的倒数
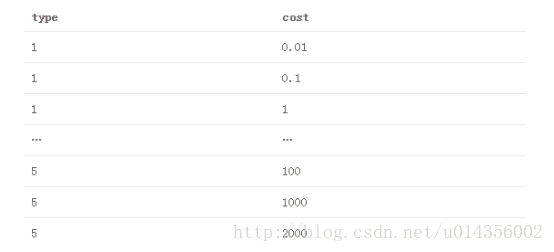
我们将测试的参数组合网格是5个列出的SVM类型的笛卡尔乘积，成本值为（.01，.1，10，100，1000，2000）。 那是

---

---

使用与我们的K最近邻模型相同的CV +网格搜索方法，这里我们找到最好的超参数为type = 4，cost = 1000。再次，我们使用这些参数训练的模型，并对测试数据集进行预测。这将在测试数据集上给我们约61％的CV分类精度和78％的分类准确性。

堆叠（元组合）

让我们来看看每个模型分为Bob，Sue，Mark或Kate的板区域。

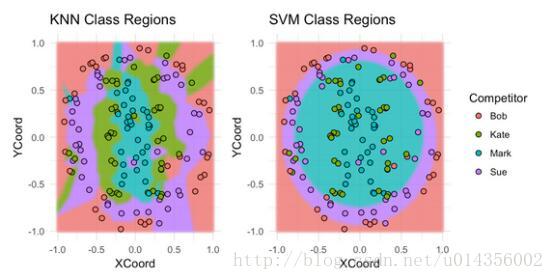
不出所料，SVM在分类Bob的投掷和Sue的投掷方面做得很好，但是在分类Kate的投掷和Mark的投掷方面做得不好。对于最近邻模型，情况正好相反。 提示：堆叠这些模型可能会卓有成效。
一共有几个思考如何实现堆叠的派别。在我们的示例问题中我是根据自己的喜好来应用的：
1.将训练数据分成五个交叉测试

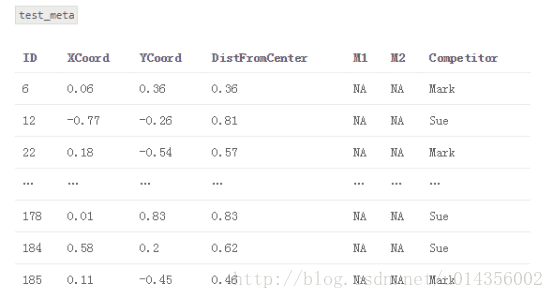
2.创建一个名为“train_meta”的数据集，其具有与训练数据集相同的行ID和交叉ID、空列M1和M2。 类似地，创建一个名为“test_meta”的数据集，其具有与测试数据集相同的行ID、空列M1和M2

---

3.对于每个交叉测试
{Fold1，Fold2，… Fold5}
3.1组合其他四个交叉用作训练交叉

3.2对于每个基本模型
M1：K-最近邻（k = 1）
M2：支持向量机（type = 4，cost = 1000）
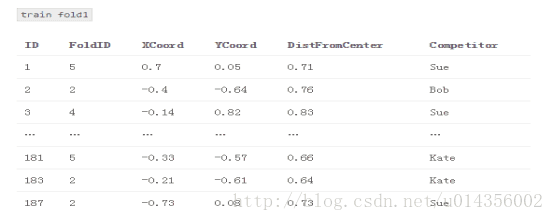
3.2.1将基本模型交叉训练，并在交叉测试进行预测。 将这些预测存储在train_meta中以用作堆叠模型的特征
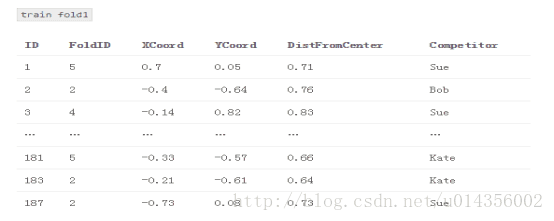
train_meta与M1和M2填补fold1

4.将每个基本模型拟合到完整训练数据集，并对测试数据集进行预测。 将这些预测存储在test_meta内

5.使用M1和M2作为特征，将新模型S（即，堆叠模型）适配到train_meta，可选地，包括来自原始训练数据集或特征工程的其他特征。
S：逻辑回归（来自LiblineaR包，类型= 6，成本= 100）。 适配train_meta
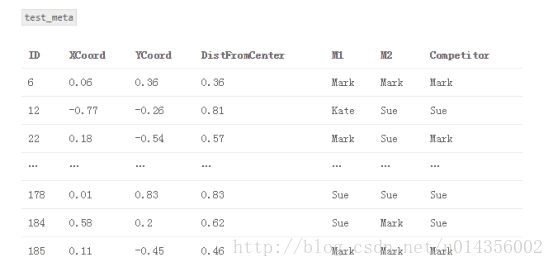
6.使用堆叠模型S对test_meta进行最终预测
test_meta与堆叠模型预测

主要观点是，我们使用基础模型的预测作为堆叠模型的特征（即元特征）。 因此，堆叠模型能够辨别哪个模型表现良好，哪个模型表现不佳。还要注意的是，train_meta的行i中的元特征不依赖于行i中的目标值，因为它们是在使用基本模型拟合过程中排除target_i的信息中产生的。
或者，我们可以在测试数据集适合每个交叉测试之后立即使用每个基本模型进行预测。 在我们的例子中，这将产生五个K-最近邻模型和五个SVM模型的测试集预测。然后，我们将平均每个模型的预测以生成我们的M1和M2元特征。 这样做的一个好处是，它比第一种方法耗时少（因为我们不必在整个训练数据集上重新训练每个模型）。 它也有助于我们的训练元特征和测试元特征遵循类似的分布。然而，测试元M1和M2在第一种方法中可能更准确，因为每个基础模型在全训练数据集上训练（相对于训练数据集的80％，在第二方法中为5次）。
堆栈模型超参数调优
那么，如何调整堆叠模型的超参数？ 关于基本模型，就像我们以前做的，我们可以使用交叉验证+网格搜索调整他们的超参数。 我们使用什么交叉并不重要，但使用我们用于堆叠的相同交叉通常很方便。调整堆叠模型的超参数是让事情变得有趣的地方。在实践中，大多数人（包括我自己）只需使用交叉验证+网格搜索，使用相同的精确CV交叉用于生成元特征。 这种方法有一个微妙的缺陷 - 你能找到它吗？
事实上，在我们的堆叠CV过程中有一点点数据泄漏。 想想堆叠模型的第一轮交叉验证。我们将模型S拟合为{fold2，fold3，fold4，fold5}，对fold1进行预测并评估效果。但是{fold2，fold3，fold4，fold5}中的元功能取决于fold1中的目标值。因此，我们试图预测的目标值本身就嵌入到我们用来拟合我们模型的特征中。这是泄漏，在理论上S可以从元特征推导出关于目标值的信息，其方式将使其过拟合训练数据，而不能很好地推广到袋外样本。 然而，你必须努力工作来想出一个这种泄漏足够大、导致堆叠模型过度拟合的例子。 在实践中，每个人都忽略了这个理论上的漏洞（坦白地说，我认为大多数人不知道它甚至存在！）
堆叠模型选择和特性
你如何知道选择何种型号作为堆叠器以及元特征要包括哪些功能？ 在我看来，这更像是一门艺术而不是一门科学。 你最好的办法是尝试不同的东西，熟悉什么是有效的，什么不是。另一个问题是，除了元特征，你应该为堆叠模型包括什么其他功能（如果有）？这也是一种艺术。看看我们的例子，很明显，DistFromCenter在确定哪个模型将会很好地发挥作用。KNN似乎在分类投掷于中心附近的飞镖上做得更好，SVM模型在分类远离中心的飞镖上表现得更好。 让我们来看看使用逻辑回归来堆叠我们的模型。 我们将使用基本模型预测作为元特征，并使用DistFromCenter作为附加功能。
果然，堆叠模型的性能优于两种基本模型 - 75％CV精度和86％测试精度。 就像我们对基本模型一样，现在让我们来看看它的覆盖训练数据的分类区域。

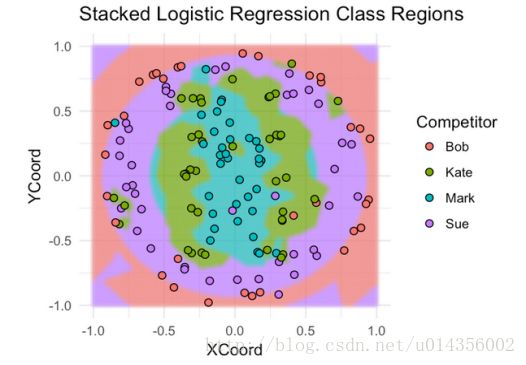
这里的好处是，逻辑回归堆叠模型捕获每个基本模型的最好的方面，这就是为什么它的执行优于任何孤立的基本模型。
实践中的堆叠
为了包装，让我们来谈谈如何、何时、以及为什么在现实世界中使用堆叠。 就个人而言，我大多在Kaggle的机器学习竞赛中使用堆叠。一般来说，堆叠产生小的收益与大量增加的复杂性不值得为大多数企业使用。 但堆叠几乎总是富有成果，所以它几乎总是用于顶部Kaggle解决方案。 事实上，当你有一队人试图在一个模型上合作时，堆叠对Kaggle真的很有效。采用一组单独的交叉，然后每个团队成员使用那些交叉建立他们自己的模型。 然后每个模型可以使用单个堆叠脚本组合。这是极好的，因为它防止团队成员踩在彼此的脚趾，尴尬地试图将他们的想法拼接到相同的代码库。
最后一位。 假设我们有具有（用户，产品）对的数据集，并且我们想要预测用户在购买给定产品的情况下，他/她与该产品一起展示广告的几率。一个有效的功能可能是，使用培训数据，有多少百分比的产品广告给用户，而他实际上在过去就已经购买？因此，对于训练数据中的样本（user1，productA），我们要解决一个像UserPurchasePercentage这样的功能，但是我们必须小心，不要在数据中引入泄漏。 我们按照接下来这样做：
1.将训练数据拆分成交叉
2.对于每个交叉测试
1.标识交叉测试中的唯一一组用户
2.使用剩余的交叉计算UserPurchasePercentage（每个用户购买的广告产品的百分比）
3.通过（fold id，用户id）将UserPurchasePercentage映射回培训数据
现在我们可以使用UserPurchasePercentage作为我们的梯度提升模型（或任何我们想要的模型）的一个特性。我们刚刚做的是有效地建立一个预测模型，基于user_i在过去购买的广告产品的百分比，预测他将购买product_x的概率，并使用这些预测作为我们的真实模型的元特征。这是一个微妙而有效并且我经常在实践和Kaggle实现的有效的堆叠形式 - 。