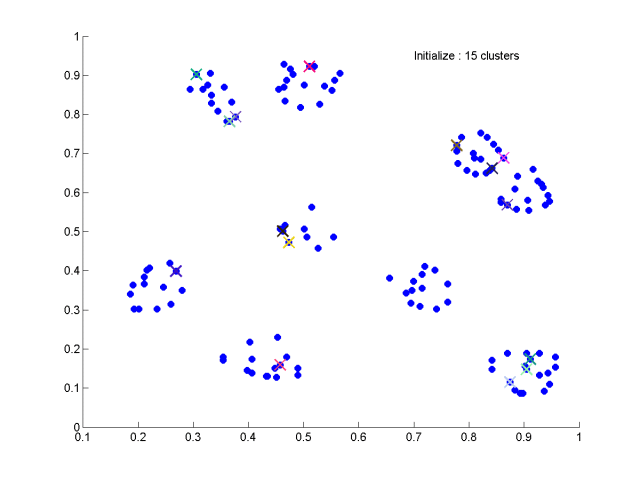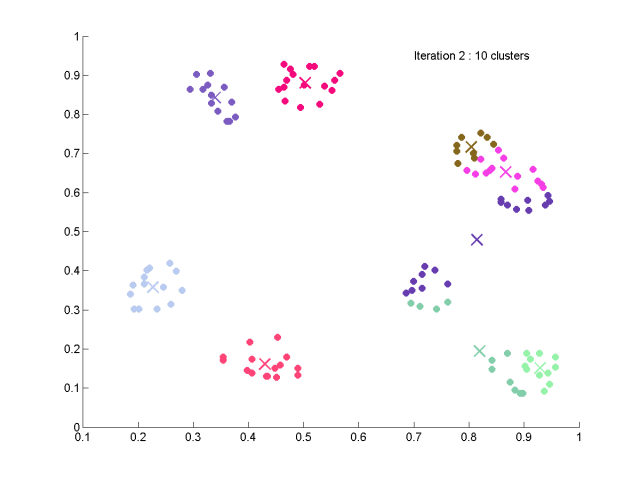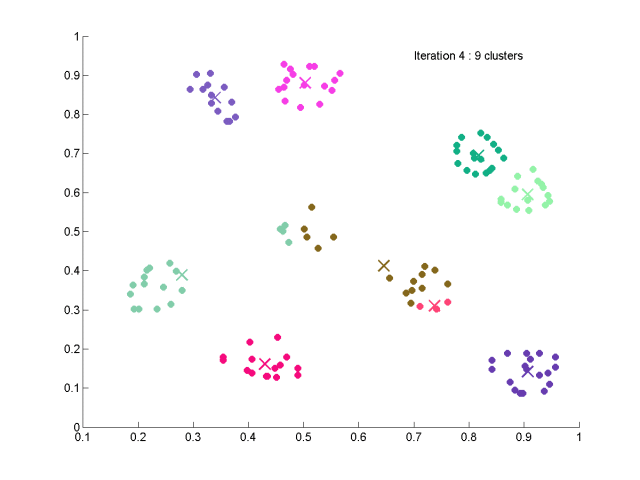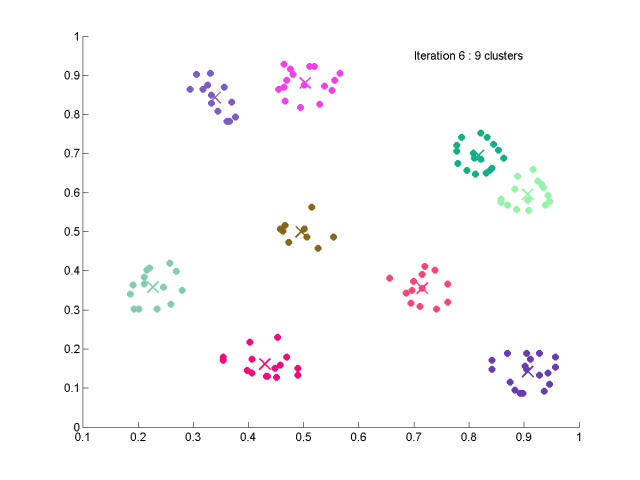
isodata聚类算法的实现

ISODATA算法是在k-均值算法的基础上，增加对聚类结果的“合并”和“分裂”两个操作，并设定算法运行控制参数的一种聚类算法。迭代次数会影响最终结果，迭代参数选择很重要。

算法步骤   如下：

①初始化

设定控制参数：

c：预期的类数；

Nc：初始 聚类中心个数（可以不等于c）；

TN：每一类中允许的最少样本数目（若少于此数，就不能单独成为一类）；

TE：类内各特征分量分布的相对标准差上限（大于此数就分裂）；

TC：两类中心间的最小距离下限（若小于此数，这两类应合并）；

NT：在每次 迭代中最多可以进行“合并”操作的次数；

NS：允许的最多迭代次数。

选定初始 聚类中心

②按最近邻规则将样本集{xi}中每个样本分到某一类中

③依据TN判断合并：如果类ωj中样本数nj< TN，则取消该类的中心zj，Nc=Nc-1，转至② 。

④计算分类后的参数：各类重心、类内平均距离

   

及总体平均距离

 

计算各类的重心：

计算各类中样本到类心的平均距离：

计算各个样本到其类内中心的总体平均距离：

⑤判断停止、分裂或合并。

a、若 迭代次数Ip =NS，则算法结束；

b、若Nc ≤c/2，则转到⑥ （将一些类分裂）；

c、若Nc ≥2c，则转至⑦ （跳过分裂处理）；

d、若c/2< Nc<2c，当迭代次数Ip是奇数时转至⑥ （分裂处理）；迭代次数Ip是偶数时转至⑦ （合并处理）。

⑥分裂操作

计算各类内样本到类中心的标准差向量

σj=(σ1j, σ2j,…., σnj)T , j=1,2,…..,Nc

计算其各个分量。

求出每一类内标准差向量σj中的最大分量

 

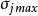
若有某一类中最大分量大于TE，同时又满足下面两个条件之一：

a、

   

>

   

和

   

>2(TN+1) b、Nc

   

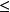c/2

则将该类ωj分裂为两个类，原zj取消且令Nc=Nc+1。

两个新类的中心zj+和zj-分别是在原zj中相应于

   

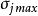的分量加上和减去

   

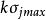，而起它分量不变，其中0

分裂后，Ip=Ip+1, 转至②。

⑦合并操作

计算各类中心间的距离Dij，i=1,2,…,Nc-1; j=1,2,…,Nc

依据TC判断合并。将Dij与TC比较，并将小于TC的那些Dij按递增次序排列，取前NT个。

从最小的Dij开始，将相应的两类合并，并计算合并后的 聚类中心。

在一次 迭代中，某一类最多只能合并一次。

Nc=Nc-已并掉的类数。

⑧如果迭代次数Ip=NS或过程收敛，则算法结束。否则，Ip=Ip+1，若需要调整参数，则转至①；若不改变参数，则转至②；

具体可参见我上传的资料 isodata聚类算法步骤说明

// isodata-cluster.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include
#include
#include
#include
#include
#include
#include 
using namespace std;

class isodata
{
private:
	unsigned int K;// 所想要分成的类别数
	unsigned int thetaN;//一个类别至少应具有的样本数目，如小于此数就不作为一个独立的聚类
	double theta_c;// 聚类中心之间距离的最小值,即归并系数，如小于此数，两个聚类进行合并
	double theta_s;// 一个类别中样本标准差最大值
	unsigned int maxcombine;// 每次迭代最多可归并对数
	unsigned int maxiteration;// 最大迭代次数
	unsigned int dim;
	double meandis;
	double alpha;
	unsigned int current_iter;
	vector>dataset;
	typedef vector Centroid;
	struct Cluster
	{
		vectorclusterID;
		Centroid center;
		double inner_meandis;
		vectorsigma;
	};
	vectorclus;
private:
	void init();
	void assign();
	void check_thetaN();
	void update_centers();
	void update_center(Cluster &aa);
	void update_sigma(Cluster &aa);
	void calmeandis();
	void choose_nextstep();
	double distance(const Centroid ¢er, const int k);
	double distance(const Centroid &cen1, const Centroid &cen2);
	void split(const int kk);
	void check_for_split();
	void merge(const int k1, const int k2);
	void check_for_merge();
	void prepare_for_next_itration();
	void show_result();
public:
	isodata()
	{
		time_t t;
		srand(time(&t));
	}
	void generate_data();
	void apply();
	void set_paras();
};

void isodata::show_result()
{
	int num = 0;
	for (int i = 0; i < clus.size(); i++)
	{
		char string[100];
		sprintf(string, "第个%d簇：", i);
		cout << string << endl;
		cout << "中心为 (" << clus[i].center[0] << ","
			<< clus[i].center[1] << ")" << endl;
		for (int j = 0; j < clus[i].clusterID.size(); j++)
		{
			sprintf(string, "编号%d   ", clus[i].clusterID[j]);
			cout << string << "(" << dataset[clus[i].clusterID[j]][0] << ","
				<< dataset[clus[i].clusterID[j]][1] << ")" << endl;
			num++;
		}

		cout << endl << endl;
	}

	_ASSERTE(num == dataset.size());


}


void isodata::generate_data()
{
	int datanums = 100;
	dim = 2;
	for (int i = 0; i < datanums; i++)
	{
		vectordata;
		data.resize(dim);
		for (int j = 0; j < dim; j++)
			data[j] = double(rand()) / RAND_MAX * 100;
		dataset.push_back(data);
	}
}

void isodata::set_paras()
{
	K = 5;
	theta_c = 5;
	theta_s = 0.01;
	maxiteration = 10;
	maxcombine = 2;
	thetaN = 5;
	alpha = 0.3;
}

void isodata::prepare_for_next_itration()
{
	for (int i = 0; i < clus.size(); i++)
		clus[i].clusterID.clear();
}

void isodata::apply()
{
	init();
	while (current_iter < maxiteration)
	{
		current_iter++;
		assign();
		check_thetaN();
		update_centers();
		calmeandis();
		choose_nextstep();
		if (current_iter < maxiteration)
			prepare_for_next_itration();
	}
	show_result();
}

double isodata::distance(const Centroid &cen, const int k)
{
	double dis = 0;
	for (int i = 0; i < dim; i++)
		dis += pow(cen[i] - dataset[k][i], 2);
	return sqrt(dis);
}

double isodata::distance(const Centroid ¢er1, const Centroid& center2)
{
	double dis = 0;
	for (int i = 0; i < dim; i++)
		dis += pow(center1[i] - center2[i], 2);
	return sqrt(dis);
}

/*第一步：输入N个模式样本{xi, i = 1, 2, …, N}
预选Nc个初始聚类中心*/
void isodata::init()
{
	clus.resize(K);
	setaa;
	for (int i = 0; i < K; i++)
	{
		clus[i].center.resize(dim);
		int id = double(rand()) / RAND_MAX*dataset.size();
		while (aa.find(id) != aa.end())
		{
			id = double(rand()) / RAND_MAX*dataset.size();
		}
		aa.insert(id);
		for (int j = 0; j < dim; j++)
			clus[i].center[j] = dataset[id][j];
	}
}

/*第二步：将N个模式样本分给最近的聚类Sj */
void isodata::assign()
{
	for (int i = 0; i < dataset.size(); i++)
	{
		double mindis = 100000000;
		int th = -1;
		for (int j = 0; j < clus.size(); j++)
		{
			double dis = distance(clus[j].center, i);
			if (dis < mindis)
			{
				mindis = dis;
				th = j;
			}
		}
		clus[th].clusterID.push_back(i);
	}
}

/*第三步：如果Sj中的样本数目Sj<θN，
则取消该样本子集，此时Nc减去1*/
void isodata::check_thetaN()
{
	vectortoerase;
	for (int i = 0; i < clus.size(); i++)
	{
		if (clus[i].clusterID.size() < thetaN)
		{
			toerase.push_back(i);
			for (int j = 0; j < clus[i].clusterID.size(); j++)
			{
				double mindis = 10000000;
				int th = -1;
				for (int m = 0; m < clus.size(); m++)
				{
					if (m == i)
						continue;
					double dis = distance(clus[m].center,
						clus[i].clusterID[j]);
					if (dis < mindis)
					{
						mindis = dis;
						th = m;
					}
				}
				clus[th].clusterID.push_back(
					clus[i].clusterID[j]);
			}
			clus[i].clusterID.clear();
		}
	}
	for (vector::iterator it = clus.begin(); it != clus.end();)
	{
		if (it->clusterID.empty())
			it = clus.erase(it);
		else
			it++;
	}
}

void isodata::update_center(Cluster &aa)
{
	Centroid temp;
	temp.resize(dim);
	for (int j = 0; j < aa.clusterID.size(); j++)
	{
		for (int m = 0; m < dim; m++)
			temp[m] += dataset[aa.
			clusterID[j]][m];
	}
	for (int m = 0; m < dim; m++)
		temp[m] /= aa.clusterID.size();
	aa.center = temp;

}

/*第四步：修正各聚类中心*/
void isodata::update_centers()
{
	for (int i = 0; i < clus.size(); i++)
	{
		update_center(clus[i]);
	}
}
void isodata::update_sigma(Cluster&bb)
{
	bb.sigma.clear();
	bb.sigma.resize(dim);
	for (int j = 0; j < bb.clusterID.size(); j++)
		for (int m = 0; m < dim; m++)
			bb.sigma[m] += pow(bb.center[m] -
			dataset[bb.clusterID[j]][m], 2);
	for (int m = 0; m < dim; m++)
		bb.sigma[m] = sqrt(bb.sigma[m] /
		bb.clusterID.size());

}

/*五六步合并*/
/*第五步：计算各聚类域Sj中模式样本与各聚类中心间的平均距离*/
/*第六步：计算全部模式样本和其对应聚类中心的总平均距离*/
void isodata::calmeandis()
{
	meandis = 0;
	for (int i = 0; i < clus.size(); i++)
	{
		double dis = 0;
		for (int j = 0; j < clus[i].
			clusterID.size(); j++)
		{
			dis += distance(clus[i].center,
				clus[i].clusterID[j]);
		}
		meandis += dis;
		clus[i].inner_meandis = dis /
			clus[i].clusterID.size();
	}
	meandis /= dataset.size();
}


/*第七步：判别下一步进行分裂或合并或迭代运算*/
void isodata::choose_nextstep()
{
	if (current_iter == maxiteration)
	{
		theta_c = 0;
		//goto step 11
		check_for_merge();
	}
	else if (clus.size() < K / 2)
	{
		check_for_split();
	}
	else if (current_iter % 2 == 0 ||
		clus.size() >= 2 * K)
	{
		//goto step 11
		check_for_merge();
	}
	else
	{
		check_for_split();
	}

}
/*八、九、十步合并为分裂操作*/
/*第八步：计算每个聚类中样本距离的标准差向量*/
/*第九步：求每一标准差向量{σj, j = 1, 2, …,
Nc}中的最大分量*/
/*第十步：分裂*/
void isodata::check_for_split()
{
	for (int i = 0; i < clus.size(); i++)
	{
		update_sigma(clus[i]);
	}
	while (true)
	{
		bool flag = false;
		for (int i = 0; i < clus.size(); i++)
		{
			for (int j = 0; j < dim; j++)
			{
				if (clus[i].sigma[j] > theta_s &&
					(clus[i].inner_meandis>meandis&&
					clus[i].clusterID.size()>
					2 * (thetaN + 1) || clus.size() < K / 2))
				{
					flag = true;
					split(i);
				}
			}
		}
		if (!flag)
			break;
		else
			calmeandis();
	}
}

void isodata::split(const int kk)
{
	Cluster newcluster;
	newcluster.center.resize(dim);

	int th = -1;
	double maxval = 0;
	for (int i = 0; i < dim; i++)
	{
		if (clus[kk].sigma[i] > maxval)
		{
			maxval = clus[kk].sigma[i];
			th = i;
		}
	}
	for (int i = 0; i < dim; i++)
	{
		newcluster.center[i] = clus[kk].center[i];
	}
	newcluster.center[th] -= alpha*clus[kk].sigma[th];
	clus[kk].center[th] += alpha*clus[kk].sigma[th];
	for (int i = 0; i < clus[kk].clusterID.size(); i++)
	{
		double d1 = distance(clus[kk].center, clus[kk].clusterID[i]);
		double d2 = distance(newcluster.center, clus[kk].clusterID[i]);
		if (d2 < d1)
			newcluster.clusterID.push_back(clus[kk].clusterID[i]);
	}
	vectorcc; cc.reserve(clus[kk].clusterID.size());
	vectoraa;
	//insert_iterator > >res_ins(aa, aa.begin()); 

	set_difference(clus[kk].clusterID.begin(), clus[kk].clusterID.end(),
		newcluster.clusterID.begin(), newcluster.clusterID.end(), inserter(aa, aa.begin()));//差集
	clus[kk].clusterID = aa;
	//应该更新meandis sigma。。。
	update_center(newcluster);
	update_sigma(newcluster);
	update_center(clus[kk]);
	update_sigma(clus[kk]);
	clus.push_back(newcluster);
}


/*第十一步：计算全部聚类中心的距离*/
/*第十二步：比较Dij 与θc 的值，将Dij <θc 的值按最小距离次序递增排列*/
/*第十三步：将距离为 的两个聚类中心 和 合并*/
void isodata::check_for_merge()
{
	vector, double>>aa;
	for (int i = 0; i < clus.size(); i++)
	{
		for (int j = i + 1; j < clus.size(); j++)
		{
			double dis = distance(clus[i].center, clus[j].center);
			if (dis < theta_c)
			{
				pairbb(i, j);
				aa.push_back(pair, double>(bb, dis));
			}
		}
	}
	// 利用函数对象实现升降排序    
	struct CompNameEx
	{
		CompNameEx(bool asce) : asce_(asce)
		{}
		bool operator()(pair, double>const& pl, pair, double>const& pr)
		{
			return asce_ ? pl.second < pr.second : pr.second < pl.second; // 《Eff STL》条款21: 永远让比较函数对相等的值返回false    
		}
	private:
		bool asce_;
	};
	sort(aa.begin(), aa.end(), CompNameEx(true));
	setbb;
	int combinenus = 0;
	for (int i = 0; i < aa.size(); i++)
	{
		if (bb.find(aa[i].first.first) == bb.end()
			&& bb.find(aa[i].first.second) == bb.end())
		{
			bb.insert(aa[i].first.first);
			bb.insert(aa[i].first.second);
			merge(aa[i].first.first, aa[i].first.second);
			combinenus++;
			if (combinenus >= maxcombine)
				break;
		}
	}
	for (vector::iterator it = clus.begin(); it != clus.end();)
	{
		if (it->clusterID.empty())
		{
			it = clus.erase(it);
		}
		else
			it++;
	}

}

void isodata::merge(const int k1, const int k2)//k1、k2顺序不能变
{
	for (int i = 0; i < dim; i++)
		clus[k1].center[i] = (clus[k1].center[i] * clus[k1].clusterID.size() +
		clus[k2].center[i] * clus[k2].clusterID.size()) /
		double(clus[k1].clusterID.size() + clus[k2].clusterID.size());
	//clus[k1].clusterID.insert(clus[k1].clusterID.end(), 
	//	clus[k2].clusterID.begin(), clus[k2].clusterID.end());
	clus[k2].clusterID.clear();
}

int _tmain(int argc, _TCHAR* argv[])
{
	/*vectoraa;
	aa.push_back(1);
	aa.push_back(2);
	aa.push_back(3);
	aa.push_back(4);
	aa.push_back(5);
	for (vector::iterator it = aa.begin(); it != aa.end(); )
	{
	cout << *it << endl;
	//it = aa.erase(it);
	//if (it == aa.end())
	//	break;
	if (*it > 3)
	{
	it = aa.insert(it+1, 2);
	cout << *it << endl;
	}
	else
	it++;
	}*/
	isodata iso;
	iso.generate_data();
	iso.set_paras();
	iso.apply();


	system("pause");
	return 0;
}

下面是结果，100个数据，共生成10个簇，结果比kmeans应该好一些