深入BRDF和PBR大作战!(之二):微面理论
微面理论
PBR(Physically Based Rendering)让我们的渲染不再依赖经验模型,而是真正具有物理意义。其中的原因正是因为PBR的核心:微面理论(Microfacet theory)。微面理论已经是 CG 渲染以及BRDF的中心理论,SIGGRAPH也连续很多年有针对微面理论专门的学习课程。

Unreal4 引擎中,PBR渲染的地精银行Goblin,图片来自baolong zhang
不过微面理论的推导十分麻烦,在Real Time Rendering 4th上描述的篇幅也很有限1。初次接触很容易就被搞得一脸懵逼,但作为偏执狂的作者怎么能放过这一次疯狂挑战的机会!

PBR 可以通过2个参数均匀的模拟材质属性的变化
所以这一篇是:
- 微面理论介绍和证明推导
- 理解基于PBR的BRDF函数
- 推导阴影遮挡函数 G 2 G_2 G2
- 推导法向面分布NDF函数
- PBR为什么能真实的渲染光照
- 需要一些微积分和概率知识
我们先例行公事,做一些符号的定义:
- : = := := 强调这是一个定义
- ⟨ a ⋅ b ⟩ : = cos ( θ a b ) \left\langle\mathbf{a}\cdot\mathbf{b}\right\rangle :=\cos{(\theta_{ab})} ⟨a⋅b⟩:=cos(θab) ,其中 θ a b \theta_{ab} θab是 a \mathbf{a} a和 b \mathbf{b} b的夹角
- ⟨ a ⋅ b ⟩ + : = max ( 0 , cos ( θ a b ) ) \langle\mathbf{a} \cdot \mathbf{b}\rangle^+:=\max{(0,\cos{(\theta_{ab})})} ⟨a⋅b⟩+:=max(0,cos(θab)) ,其中 θ a b \theta_{ab} θab是 a \mathbf{a} a和 b \mathbf{b} b的夹角
定义

角度和向量定义
我们在上一篇里学到BRDF渲染函数公式,在对于任一个渲染片元(Rendering Patch)2:
(1) L o ( v ) = ∫ l ∈ Ω f ( l , v ) L i ( l ) ⟨ n ⋅ l ⟩ + d l L_{o}(\mathbf{v}) =\int_{\mathbf{l} \in \Omega} f(\mathbf{l}, \mathbf{v}) L_{i}(\mathbf{l})\langle\mathbf{n} \cdot \mathbf{l}\rangle^+ d \mathbf{l} \tag{1} Lo(v)=∫l∈Ωf(l,v)Li(l)⟨n⋅l⟩+dl(1)
其中 L o L_{o} Lo是光线传出的辉度(radiance)3, L i L_{i} Li光线传入的辉度, f f f是BRDF函数。
对于某一个具体的入射光线(也就是说,无论是场景中的点光源,平行光源,还是聚光灯或平面灯),对入射方向 l \mathbf{l} l进行微分:
(2) d L o ( v ) = f ( l , v ) L i ( l ) ⟨ n ⋅ l ⟩ + d l dL_{o}(\mathbf{v})= f(\mathbf{l}, \mathbf{v}) L_{i}(\mathbf{l})\langle\mathbf{n} \cdot \mathbf{l}\rangle^+ d \mathbf{l} \tag{2} dLo(v)=f(l,v)Li(l)⟨n⋅l⟩+dl(2)
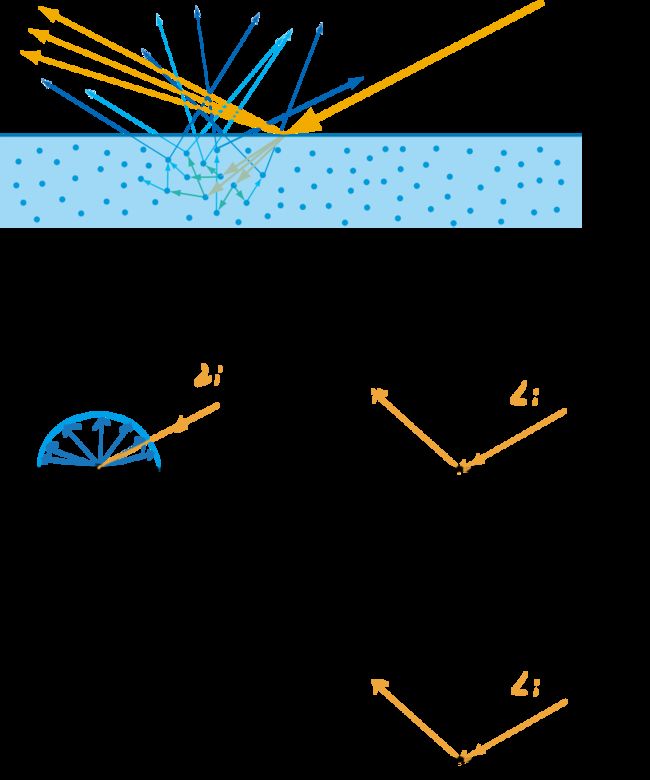
接下来我们分离了漫反射 diffuse \text{diffuse} diffuse项和高光 specular \text{specular} specular项,对于漫反射项我们把渲染材质(Material)用兰伯特表面(Lambertian Surface)近似就能得到很好的效果。然而对于高光项,我们却无法直接通过单个菲涅尔表面(Fresnel Surface)近似,具体原因不言而喻,因为菲涅尔表面仅能在 l \mathbf{l} l的反射方向上传递光线。
单个菲涅尔表面无法模拟真实的高光情况,图中红色理想菲涅尔镜面反射的光,蓝色为想要模拟出来的高光反光
先来看看最终的高光项的BRDF:
(3) f spec ( l , v ) = F ( h , l ) G 2 ( l , v , h ) D ( h ) 4 ∣ n ⋅ l ∣ ∣ n ⋅ v ∣ f_{\text { spec }}(\mathbf{l}, \mathbf{v})=\frac{F(\mathbf{h}, \mathbf{l}) G_{2}(\mathbf{l}, \mathbf{v}, \mathbf{h}) D(\mathbf{h})}{4\,|\mathbf{n} \cdot \mathbf{l}|\,| \mathbf{n} \cdot \mathbf{v}| } \tag{3} f spec (l,v)=4∣n⋅l∣∣n⋅v∣F(h,l)G2(l,v,h)D(h)(3)
其中:
- G 2 G_2 G2是遮挡阴影函数(masking shadowing function)
- D D D是法向面分布函数(normal distribution function),我们后面简称为NDF
- F F F是菲涅尔反射函数(fresnel reflectance function)在上一篇定义过
PBR的BRDF用一个兰伯特表面和多个菲涅尔表面去模拟真实情况
看到这里千万不要慌,保持镇定!虽然我知道你满脑子的问号:遮挡阴影函数是什么?法向面分布函数是什么?分母的那个 4 4 4是干啥?但只要记住了,我们的本质想法是用多个微小的菲涅尔镜面去近似真实世界的材质,这就是微面理论的核心概念,剩下的我们再一一解决!
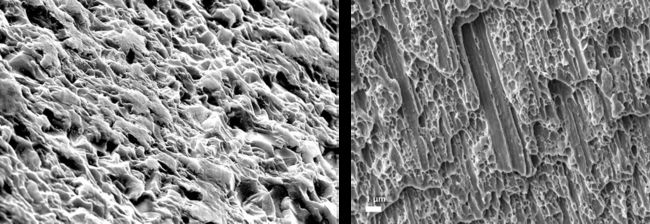
对于真实世界的物体在显微镜下观察确实是有很多微小平面组成
左图为抛光塑料表面,右图为不锈钢表面
高光项
微面化渲染片元:
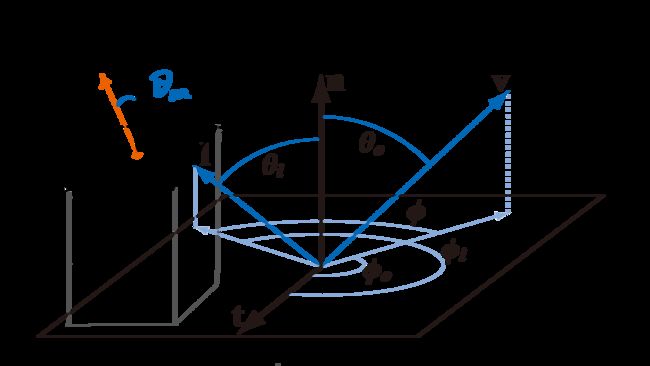
微面和渲染片元的角度向量定义
先放下高光项的公式 ( 3 ) \left(\mathrm{3}\right) (3)。首先考虑某个渲染片元(比如是材料表面的一小块且刚好投影到屏幕上的一个像素那么大)这个渲染片元法向量是 n \mathbf{n} n 。和经典的BRDF模型4不同的是,也是微面理论的第一个假设:片元中包含了多个微平面。因此对于渲染片元来说,最后向观察者 v \mathbf{v} v方向传递的光,即辉度(辐射度,radiance)3则是其微面辉度的加和:
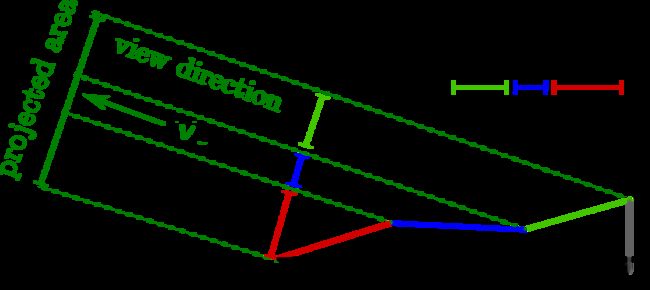
对于一个渲染片元来说,观察者方向的辉度可认为是各微面的辉度和
所以在微面理论中我们按各个微面在 v \mathbf{v} v方向投影所占的比例来计算辉度:
(4) L o ( v ) = ∫ projected area ( x ) L ( v , x ) d x ∫ projected area ( x ) d x L_\mathbf{o}(\mathbf{v})=\frac{\int \text { projected area }(x) L\left(\mathbf{v}, x\right) d x}{\int \text { projected area }(x) d x} \tag{4} Lo(v)=∫ projected area (x)dx∫ projected area (x)L(v,x)dx(4)
同时对于这个单位面积的渲染片元,在观察方向 v \mathbf{v} v的投影面积等于:
(5) projected area = v ⋅ n = cos θ o \text { projected area }=\mathbf{v} \cdot \mathbf{n}=\cos \theta_{o} \tag{5} projected area =v⋅n=cosθo(5)
法向面分布函数:
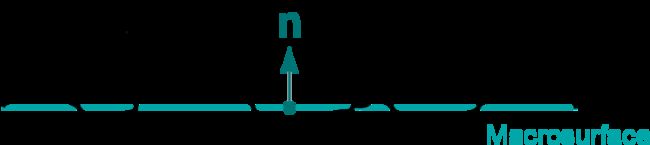
我们需要考虑对于一个单位面积上的渲染片元,朝向 m \mathbf{m} m方向上的微面面积,以便我们最后来统计这样的微面所占的比例。于是法向分布函数NDF就是这样定义的:
D ( m ) : = { 朝向 m 的微面面积 } D(\mathbf{m}) :=\{\text{朝向}\,\mathbf{m}\,\text{的微面面积}\} D(m):={朝向m的微面面积}
对于NDF有这些属性:
- 不是概率密度函数,也不是正态分布函数(要特别指出这点,被很多文稿弄错),而是一个面积的密度函数
- 0 ≤ D ( m ) ≤ ∞ 0 \leq D(\mathbf{m}) \leq \infty 0≤D(m)≤∞
- ∫ D ( m ) \int D(\mathbf{m}) ∫D(m)是所有微平面在渲染单元上的面积
- 所以 ∫ D ( m ) d m ≥ 1 \int D(\mathbf{m}) d \mathbf{m}\geq 1 ∫D(m)dm≥1 ,因此等号成立当且仅当渲染片元是一个纯平的面。
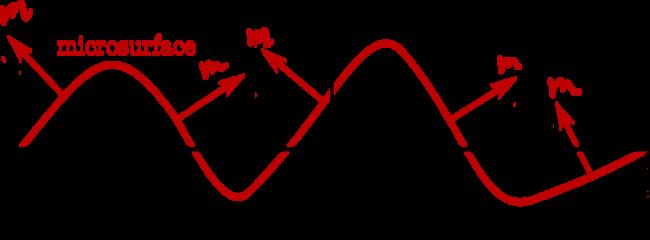
以及对于渲染片元法向方向 n \mathbf{n} n有:
∫ m ∈ Ω ⟨ m ⋅ n ⟩ D ( m ) d m = 1 \int_{\mathbf{m} \in\Omega}\left\langle\mathbf{m}\cdot\mathbf{n}\right\rangle D(\mathbf{m}) d \mathbf{m}=1 ∫m∈Ω⟨m⋅n⟩D(m)dm=1
遮挡函数:
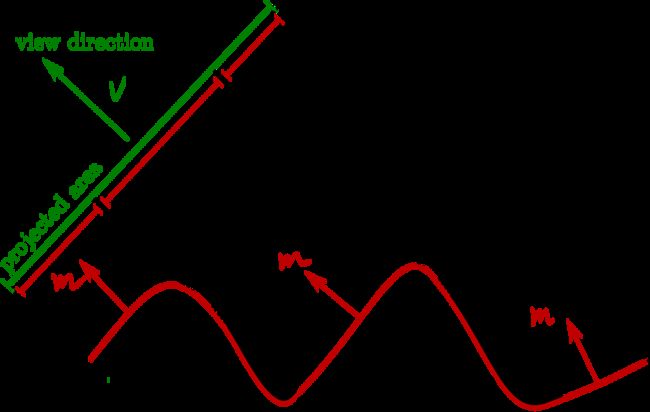
投影的面积不仅和NDF成正比以外,还要考虑微平面被遮挡的情况。如果一个微面是背向观察者或者被其他微面遮挡时,那就不会考虑在 ( 4 ) \left(\mathrm{4}\right) (4)式中贡献辉度了。因此我们要定义其被遮挡的概率函数 G 1 G_1 G1
G 1 ( m , v ) : = { 在观察者是 v 方向时 , m 方 向 面的可见概率 } G_1(\mathbf{m},\mathbf{v}):=\{\text{在观察者是}\mathbf{v} \text{方向时},\mathbf{m}方向\text{面的可见概率}\} G1(m,v):={在观察者是v方向时,m方向面的可见概率}
现在就能计算式中的投影面积了:
(6) projected area = ∫ m ∈ Ω G 1 ( v , m ) < v , m > D ( m ) d m \text { projected area }=\int_{\mathbf{m}\in\Omega} G_{1}\left(\mathbf{v}, \mathbf{m}\right)\left<\mathbf{v}, \mathbf{m}\right> D\left(\mathbf{m}\right) d \mathbf{m} \tag{6} projected area =∫m∈ΩG1(v,m)⟨v,m⟩D(m)dm(6)
结合 ( 5 ) \left(\mathrm{5}\right) (5)式就有了我们的第一个微面理论的等式:
cos θ o = ∫ Ω G 1 ( v , m ) ⟨ v ⋅ m ⟩ D ( m ) d m \cos \theta_{o}=\int_{\Omega} G_{1}\left(\mathbf{v}, \mathbf{m}\right)\left\langle\mathbf{v}\cdot \mathbf{m}\right\rangle D\left(\mathbf{m}\right) d \mathbf{m} cosθo=∫ΩG1(v,m)⟨v⋅m⟩D(m)dm
代回 ( 4 ) \left(\mathrm{4}\right) (4)式,得到:
(7) L o ( v ) = 1 cos θ o ∫ Ω L ( v , m ) G 1 ( v , m ) ⟨ v ⋅ m ⟩ D ( m ) d m L_{\mathbf{o}}\left(\mathbf{v}\right)=\frac{1}{\cos \theta_{o}} \int_{\Omega} L\left(\mathbf{v}, \mathbf{m}\right) G_{1}\left(\mathbf{v}, \mathbf{m}\right)\left\langle\mathbf{v}\cdot \mathbf{m}\right\rangle D\left(\mathbf{m}\right) d \mathbf{m} \tag{7} Lo(v)=cosθo1∫ΩL(v,m)G1(v,m)⟨v⋅m⟩D(m)dm(7)
其中分母的 1 cos θ o \frac{1}{\cos \theta_{o}} cosθo1则是 ( 4 ) \left(\mathrm{4}\right) (4)式中单位面积渲染片元在观察方向 v \mathbf{v} v的投影面积。而积分号下则是对各微面辉度的加和。

此时我们可以定义对于观察方向 o \mathbf{o} o的权重函数,以方便后面计算:
(8) D m ( m ) : = G 1 ( v , m ) ⟨ v ⋅ m ⟩ D ( m ) cos θ o D_{\mathbf{m}}\left(\mathbf{m}\right):=\frac{G_{1}\left(\mathbf{v}, \mathbf{m}\right)\left\langle\mathbf{v}\cdot \mathbf{m}\right\rangle D\left(\mathbf{m}\right)}{\cos \theta_{o}} \tag{8} Dm(m):=cosθoG1(v,m)⟨v⋅m⟩D(m)(8)
请留意 D m D_{\mathbf{m}} Dm确实是概率密度函数,因为 ∫ D m ( m ) d m = 1 \int D_{\mathbf{m}}(\mathbf{m})d\mathbf{m}=1 ∫Dm(m)dm=1,所以 ( 7 ) \left(\mathrm{7}\right) (7)式可以写成:
(9) L o ( v ) = ∫ Ω L ( v , m ) D m ( m ) d m L_\mathbf{o}\left(\mathbf{v}\right)=\int_{\Omega} L\left(\mathbf{v}, \mathbf{m}\right) D_{\mathbf{m}}\left(\mathbf{m}\right) d \mathbf{m} \tag{9} Lo(v)=∫ΩL(v,m)Dm(m)dm(9)
激活面:
对于 ( 9 ) \left(\mathrm{9}\right) (9)式,我们想知道最后的渲染结果 L o ( v ) L_\mathbf{o}\left(\mathbf{v}\right) Lo(v),可以对每个积分号下的微面应用BRDF渲染函数:
L o ( v ) = ∫ m ∈ Ω ∫ l ∈ Ω ρ μ ( v , l , m ) L i ( l ) ⟨ l ⋅ m ⟩ D m ( m ) d l d m L_\mathbf{o}(\mathbf{v})=\int_{\mathbf{m}\in\Omega}\int_{\mathbf{l}\in\Omega} \rho_{\mu}(\mathbf{v}, \mathbf{l}, \mathbf{m}) L_\mathbf{i}(\mathbf{l}) \left\langle\mathbf{l}\cdot \mathbf{m}\right\rangle D_{\mathbf{m}}(\mathbf{m}) d \mathbf{l} \,d \mathbf{m} Lo(v)=∫m∈Ω∫l∈Ωρμ(v,l,m)Li(l)⟨l⋅m⟩Dm(m)dldm
其中每个微面的BRDF函数是 ρ μ ( v , l , m ) \rho_{\mu}\left(\mathbf{v}, \mathbf{l}, \mathbf{m}\right) ρμ(v,l,m)。我们在实际渲染过程中是对每一个入射角方向 l \mathbf{l} l的光线去求值的,所以我们在这里可以对 l \mathbf{l} l进行微分:
d L o ( v ) = L i ( l ) d l ∫ m ∈ Ω ρ μ ( v , l , m ) ⟨ l ⋅ m ⟩ D m ( m ) d m dL_\mathbf{o}(\mathbf{v})=L_\mathbf{i}(\mathbf{l}) \, d \mathbf{l} \int_{\mathbf{m}\in\Omega} \rho_{\mu}(\mathbf{v}, \mathbf{l}, \mathbf{m}) \left\langle\mathbf{l}\cdot \mathbf{m}\right\rangle D_{\mathbf{m}}(\mathbf{m}) d \mathbf{m} dLo(v)=Li(l)dl∫m∈Ωρμ(v,l,m)⟨l⋅m⟩Dm(m)dm
结合 ( 2 ) \left(\mathrm{2}\right) (2)式我们就得到一个在微面理论下关于该渲染片元的BRDF:
(10) f ( l , v ) = 1 ⟨ l ⋅ n ⟩ ∫ Ω ρ μ ( v , l , m ) ⟨ l ⋅ m ⟩ D m ( m ) d m f(\mathbf{l},\mathbf{v}) = \frac{1}{\left\langle\mathbf{l}\cdot\mathbf{n}\right\rangle}\int_{\Omega} \rho_{\mu}\left(\mathbf{v}, \mathbf{l}, \mathbf{m}\right)\left\langle\mathbf{l}\cdot \mathbf{m}\right\rangle D_{\mathbf{m}}\left(\mathbf{m}\right) d \mathbf{m} \tag{10} f(l,v)=⟨l⋅n⟩1∫Ωρμ(v,l,m)⟨l⋅m⟩Dm(m)dm(10)
现在我们做出微面理论的第二个假设:所有贡献高光的微面都是菲涅尔镜面,所以只有那些和入射光线 l \mathbf{l} l和观察方向 v \mathbf{v} v的半向量 h = v + l \mathbf{h}=\mathbf{v}+\mathbf{l} h=v+l 完美对齐的那些微面才会在渲染片元的高光部分起到作用。
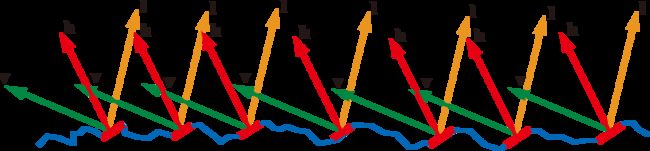
只有刚好对齐了入射光和观察者的半向量h的那些面才会贡献高光部分
我们把这些起到反射作用的微面称为当前的激活面,于是对于右边积分式就只有在 m = h \mathbf{m}=\mathbf{h} m=h时有求值的必要(你可以想象成对于半球积分仅当微分角 d m d\mathbf{m} dm扫到激活面才不是 0 0 0),所以我们完全可以把 ρ μ \rho_{\mu} ρμ用一个狄拉克函数来代替:
ρ μ ( v , l , m ) ∣ m = h = k δ h ( m ) \left.\rho_{\mu}\left(\mathbf{v}, \mathbf{l}, \mathbf{m}\right)\right|_{\mathbf{m}=\mathbf{h}}=k\, \delta_{\mathbf{h}}(\mathbf{m}) ρμ(v,l,m)∣m=h=kδh(m)
其中:
δ h ( m ) : = { ∞ if m = h 0 o t h e r w i s e \delta_{h}(\mathbf{m}) := \begin{cases} \infty &\text{if }\ \mathbf{m}=\mathbf{h}\\ 0 &\mathrm{otherwise} \end{cases} δh(m):={∞0if m=hotherwise
注意这里 δ h ( m ) \delta_{h}(\mathbf{m}) δh(m)是关于 m \mathbf{m} m的狄拉克函数,后面我们积分时要考虑。
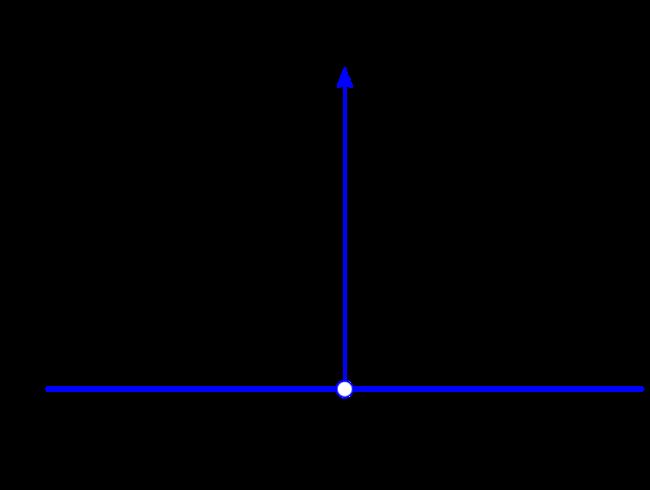
狄拉克函数
同时 ρ μ \rho_{\mu} ρμ也是菲涅尔镜面,那么对该微面求半球反射积分则有:
(11) ∫ l ∈ Ω ρ μ ( v , l , m ) ⟨ l ⋅ m ⟩ d l = ∫ h ∈ Ω k δ h ( m ) ∥ ∂ h ∂ l ∥ d l = F ( cos ( θ i ) ) \begin{aligned} \int_{\mathbf{l}\in\Omega} \rho_{\mu}\left(\mathbf{v}, \mathbf{l},\mathbf{m}\right) \left\langle\mathbf{l}\cdot \mathbf{m}\right\rangle d \mathbf{l}& =\int_{\mathbf{h}\in\Omega} k\,\delta_{\mathbf{h}}(\mathbf{m}) \left\|\frac{\partial \mathbf{h}}{\partial \mathbf{l}}\right\| d\mathbf{l} \\\\&= F(\cos(\theta_{i})) \end{aligned} \tag{11} ∫l∈Ωρμ(v,l,m)⟨l⋅m⟩dl=∫h∈Ωkδh(m)∥∥∥∥∂l∂h∥∥∥∥dl=F(cos(θi))(11)
要做几点解释:
- F F F就是我们熟悉的菲涅尔镜面反射函数,且只有在 m = h \mathbf{m}=\mathbf{h} m=h时反光,这里我们用的是 cos ( θ i ) = ⟨ l ⋅ h ⟩ \cos(\theta_{i})=\langle\mathbf{l}\cdot\mathbf{h}\rangle cos(θi)=⟨l⋅h⟩。
- 微面反射是能量守恒的,且 F ≤ 1 F \leq 1 F≤1
- ρ μ \rho_{\mu} ρμ在等式左边是关于 l \mathbf{l} l的函数,在右边是关于 m \mathbf{m} m的函数,因此要代入Jacobian系数 ∥ ∂ h ∂ l ∥ \left\|\frac{\partial \mathbf{h}}{\partial \mathbf{l}}\right\| ∥∥∂l∂h∥∥
- 有些文献中积分的是 d v d\mathbf{v} dv。这是因为BRDF的Helmholtz对称性即:
f ( l , v ) = f ( v , l ) f(\mathbf{l}, \mathbf{v})=f(\mathbf{v}, \mathbf{l}) f(l,v)=f(v,l)
所以我们积分哪个都是一样的。
所以剩下最后的问题就是怎么找到Jacobian系数。要时刻记住微面理论的假设只有激活面的辉度贡献才不是0,所以我们只有考虑在这个条件下的计算Jacobian系数
Jacobian系数推导:
看到 ( 11 ) \left(\mathrm{11}\right) (11)式右边,由于有狄拉克函数的存在,所以只有在积分函数“扫“到 m = h \mathbf{m}=\mathbf{h} m=h的时刻,狄拉克函数才不是 0 0 0。所以我们只需要求此时刻Jacobian系数的 ∥ ∂ h ∂ l ∥ \left\|\frac{\partial \mathbf{h}}{\partial \mathbf{l}}\right\| ∥∥∂l∂h∥∥ 值
我们把此时的向量 l \mathbf{l} l移到向量 v \mathbf{v} v的末端,令 h s = l + v \mathbf{h_s}=\mathbf{l}+\mathbf{v} hs=l+v。根据前面的描述,此时的 h \mathbf{h} h正好是和 h s \mathbf{h_s} hs方向一致的单位向量。
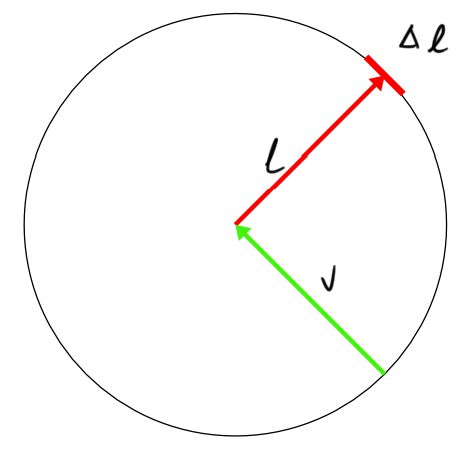
我们再来考虑此时的 Δ l \Delta{\mathbf{l}} Δl
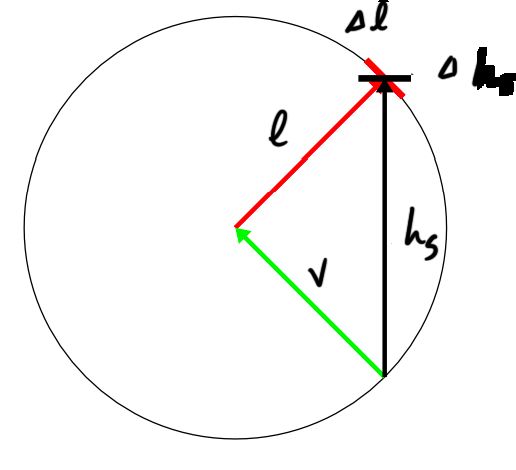
对于此时刻的 Δ h s \Delta{\mathbf{h_s}} Δhs和 Δ l \Delta{\mathbf{l}} Δl有如下关系:

也就是:
∣ Δ h s ∣ = ∣ h ⋅ l ∣ ∣ Δ l ∣ |\Delta{\mathbf{h_s}}|=|\mathbf{h}\cdot\mathbf{l}||\Delta{\mathbf{l}}| ∣Δhs∣=∣h⋅l∣∣Δl∣
因此对于 h \mathbf{h} h有:
(12) ∣ Δ h ∣ = ∣ h ⋅ l ∣ ∥ h s ∥ 2 ∣ Δ l ∣ |\Delta{\mathbf{h}}|=\frac{|\mathbf{h}\cdot\mathbf{l}|}{\|\mathbf{h_s}\|^2}|\Delta{\mathbf{l}}|\tag{12} ∣Δh∣=∥hs∥2∣h⋅l∣∣Δl∣(12)
然后:
∣ ∣ h s ∣ ∣ = ∣ ( l + v ) ⋅ h ∣ = ∣ 2 h ⋅ l ∣ \begin{aligned} ||\mathbf{h_s}||&=|(\mathbf{l}+\mathbf{v})\cdot\mathbf{h}| \\\\&=|2\mathbf{h}\cdot\mathbf{l}| \end{aligned} ∣∣hs∣∣=∣(l+v)⋅h∣=∣2h⋅l∣
∣ ∣ h s ∣ ∣ 2 = 4 ∣ h ⋅ l ∣ 2 ||\mathbf{h_s}||^2=4\,|\mathbf{h}\cdot\mathbf{l}|^2 ∣∣hs∣∣2=4∣h⋅l∣2
代入 ( 12 ) \left(\mathrm{12}\right) (12)式,稍作整理并求 Δ h / Δ l \Delta\mathbf{h}/\Delta\mathbf{l} Δh/Δl的极限,则有:
∥ ∂ h ∂ l ∥ = 1 4 ∣ l ⋅ h ∣ \left\|\frac{\partial \mathbf{h}}{\partial \mathbf{l}}\right\|=\frac{1}{4\left|\mathbf{l} \cdot \mathbf{h}\right|} ∥∥∥∥∂l∂h∥∥∥∥=4∣l⋅h∣1
PBR的高光项公式:
我们最后求的这个系数是: ∥ ∂ h ∂ l ∥ = 1 4 ∣ l ⋅ h ∣ \left\|\frac{\partial \mathbf{h}}{\partial \mathbf{l}}\right\|=\frac{1}{4\left|\mathbf{l} \cdot \mathbf{h}\right|} ∥∥∂l∂h∥∥=4∣l⋅h∣1,回到 ( 11 ) \left(\mathrm{11}\right) (11)式,狄拉克函数和积分号是可以消去了,所以我们的激活面BRDF是:
ρ μ ( v , l , m ) = ∥ ∂ h ∂ l ∥ F ( v ⋅ h ) δ h ( m ) ∣ l ⋅ h ∣ = F ( v ⋅ h ) δ h ( m ) 4 ∣ l ⋅ h ∣ 2 \begin{aligned} \rho_{\mu}\left(\mathbf{v},\mathbf{l},\mathbf{m}\right) &= \left\|\frac{\partial \mathbf{h}}{\partial \mathbf{l}}\right\| \frac{F\left(\mathbf{v}\cdot \mathbf{h}\right) \delta_{\mathbf{h}}\left(\mathbf{m}\right)}{\left|\mathbf{l} \cdot \mathbf{h}\right|} \\ & =\frac{F\left(\mathbf{v}\cdot \mathbf{h}\right) \delta_{\mathbf{h}}\left(\mathbf{m}\right)}{4\left|\mathbf{l} \cdot \mathbf{h}\right|^{2}} \end{aligned} ρμ(v,l,m)=∥∥∥∥∂l∂h∥∥∥∥∣l⋅h∣F(v⋅h)δh(m)=4∣l⋅h∣2F(v⋅h)δh(m)
太好了,绕了一大圈我们终于可以代回 ( 10 ) \left(\mathrm{10}\right) (10)式了,可以得到我们在微面理论下渲染片元的BRDF:
f ( l , v ) = 1 ⟨ l ⋅ n ⟩ ∫ Ω F ( v , h ) δ h ( m ) 4 ∣ l ⋅ h ∣ 2 ⟨ l ⋅ m ⟩ D m ( m ) d m f(\mathbf{l},\mathbf{v}) = \frac{1}{\left\langle\mathbf{l}\cdot\mathbf{n}\right\rangle}\int_{\Omega} \frac{F\left(\mathbf{v}, \mathbf{h}\right) \delta_{\mathbf{h}}\left(\mathbf{m}\right)}{4\left|\mathbf{l} \cdot \mathbf{h}\right|^{2}} \left\langle\mathbf{l}\cdot \mathbf{m}\right\rangle D_{\mathbf{m}}(\mathbf{m}) d \mathbf{m} f(l,v)=⟨l⋅n⟩1∫Ω4∣l⋅h∣2F(v,h)δh(m)⟨l⋅m⟩Dm(m)dm
根据 ( 8 ) \left(\mathrm{8}\right) (8)式,把 D m ( m ) D_{\mathbf{m}}(\mathbf{m}) Dm(m)展开:
f ( l , v ) = 1 ⟨ l ⋅ n ⟩ ∫ m ∈ Ω F ( v ⋅ h ) δ h ( m ) 4 ∣ l ⋅ h ∣ 2 ⟨ l ⋅ m ⟩ G 1 ( v ⋅ m ) ⟨ v ⋅ m ⟩ D ( m ) ⟨ v ⋅ n ⟩ d m = F ( v ⋅ h ) 4 ⟨ l ⋅ n ⟩ ∣ l ⋅ h ∣ 2 ⟨ l ⋅ h ⟩ G 1 ( v ⋅ h ) ⟨ v ⋅ h ⟩ D ( h ) ⟨ v ⋅ n ⟩ \begin{aligned} f(\mathbf{l},\mathbf{v}) &= \frac{1}{\left\langle\mathbf{l}\cdot \mathbf{n}\right\rangle} \int_{\mathbf{m}\in\Omega} \frac{F\left(\mathbf{v}\cdot \mathbf{h}\right) \delta_{\mathbf{h}}\left(\mathbf{m}\right)}{4\left|\mathbf{l} \cdot \mathbf{h}\right|^{2}} \left\langle\mathbf{l}\cdot \mathbf{m}\right\rangle \frac{G_{1}\left(\mathbf{v}\cdot \mathbf{m}\right)\left\langle\mathbf{v}\cdot \mathbf{m}\right\rangle D\left(\mathbf{m}\right)}{\left\langle\mathbf{v}\cdot \mathbf{n}\right\rangle} d \mathbf{m} \\\\ &={} \frac{F\left(\mathbf{v}\cdot \mathbf{h}\right) }{4\left\langle\mathbf{l}\cdot \mathbf{n}\right\rangle\left|\mathbf{l} \cdot \mathbf{h}\right|^{2}} \left\langle\mathbf{l}\cdot \mathbf{h}\right\rangle \frac{G_{1}\left(\mathbf{v}\cdot \mathbf{h}\right)\left\langle\mathbf{v}\cdot \mathbf{h}\right\rangle D\left(\mathbf{h}\right)}{\left\langle\mathbf{v}\cdot \mathbf{n}\right\rangle} \end{aligned} f(l,v)=⟨l⋅n⟩1∫m∈Ω4∣l⋅h∣2F(v⋅h)δh(m)⟨l⋅m⟩⟨v⋅n⟩G1(v⋅m)⟨v⋅m⟩D(m)dm=4⟨l⋅n⟩∣l⋅h∣2F(v⋅h)⟨l⋅h⟩⟨v⋅n⟩G1(v⋅h)⟨v⋅h⟩D(h)
因为 ⟨ l ⋅ h ⟩ = ⟨ v ⋅ h ⟩ \left\langle\mathbf{l}\cdot\mathbf{ h}\right\rangle=\left\langle\mathbf{v}\cdot\mathbf{h}\right\rangle ⟨l⋅h⟩=⟨v⋅h⟩最后则有:
f ( l , v ) = F ( v , h ) G 1 ( v , h ) D ( h ) 4 ∣ n ⋅ v ∣ ∣ n ⋅ l ∣ f(\mathbf{l},\mathbf{v}) =\frac{F\left(\mathbf{v}, \mathbf{h}\right) G_{1}\left(\mathbf{v}, \mathbf{h}\right) D\left(\mathbf{h}\right)}{4\left|\mathbf{n} \cdot \mathbf{v}\right|\left|\mathbf{n} \cdot \mathbf{l}\right|} f(l,v)=4∣n⋅v∣∣n⋅l∣F(v,h)G1(v,h)D(h)
Smith遮挡阴影函数
在微面理论中的第三个假设是:每一个微面的法向和位置都是独立的(independent),虽然这个假设和实际情况略有不同,即实际情况更准确应该微面是自相关(autocorrelation)的。但在实际应用中我们发现仍然能非常好的拟合现实的数据。
真实情况下的微面是一个随机过程,autocorrelation不为0(左图)
为了推出Smith G1函数,需要假设每一个微面高度和朝向都是不相关的(右图)
那么对于 G 1 ( v , m ) G_{1}(\mathbf{v}, \mathbf{m}) G1(v,m) 函数,除了在 m \mathbf{m} m是背向 v \mathbf{v} v的情况以外,对于 m \mathbf{m} m也是不依赖的
我们现在回到上面的 ( 6 ) \left(\mathrm{6}\right) (6)式,积分号那里开始,我们把和 m \mathbf{m} m不依赖的遮挡函数定义为 G 1 + G1^+ G1+:
(13) ∫ Ω G 1 ( v , m ) ⟨ v ⋅ m ⟩ D ( m ) d m = ∫ Ω χ + ( v ⋅ m ) G 1 ( v , m ) d m ∫ Ω χ + ( v ⋅ m ) d m ∫ Ω ⟨ v ⋅ m ⟩ D ( m ) d m = G 1 + ( v ) ∫ Ω ⟨ v ⋅ m ⟩ D ( m ) d m \begin{aligned} &\int_{\Omega} G_{1}\left(\mathbf{v}, \mathbf{m}\right)\left\langle\mathbf{v}\cdot \mathbf{m}\right\rangle D\left(\mathbf{m}\right) d \mathbf{m} \\\\&\qquad=\frac{\int_{\Omega} \chi^{+}\left(\mathbf{v} \cdot \mathbf{m}\right) G_{1}\left(\mathbf{v}, \mathbf{m}\right) d \mathbf{m}}{\int_{\Omega} \chi^{+}\left(\mathbf{v} \cdot \mathbf{m}\right) d \mathbf{m}} \int_{\Omega}\left\langle\mathbf{v}\cdot \mathbf{m}\right\rangle D\left(\mathbf{m}\right) d \mathbf{m} \\\\&\qquad=G_{1}^{+}\left(\mathbf{v}\right) \int_{\Omega}\left\langle\mathbf{v}\cdot \mathbf{m}\right\rangle D\left(\mathbf{m}\right) d \mathbf{m} \end{aligned} \tag{13} ∫ΩG1(v,m)⟨v⋅m⟩D(m)dm=∫Ωχ+(v⋅m)dm∫Ωχ+(v⋅m)G1(v,m)dm∫Ω⟨v⋅m⟩D(m)dm=G1+(v)∫Ω⟨v⋅m⟩D(m)dm(13)
这里要解释几点:
- 因为 G 1 + ( v ) G1^+(\mathbf{v}) G1+(v)独立于 m \mathbf{m} m,所以也就不用写在积分号下了。
- χ + \chi^{+} χ+是Heaviside阶跃函数
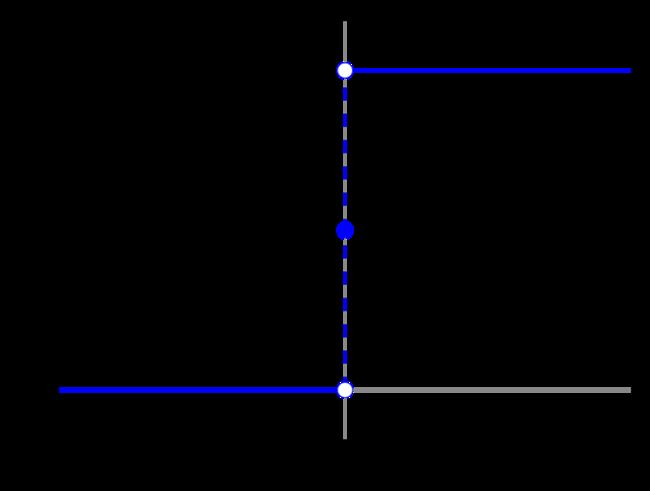
阶跃函数
因此我们计算的 G 1 + G_{1}^{+} G1+其实是计算的是没有被遮挡面的平均值:
G 1 + ( v ) = ∫ Ω χ + ( v ⋅ m ) G 1 ( v , m ) d m ∫ Ω χ + ( v ⋅ m ) d m G_{1}^{+}\left(\mathbf{v}\right)=\frac{\int_{\Omega} \chi^{+}\left(\mathbf{v} \cdot \mathbf{m}\right) G_{1}\left(\mathbf{v}, \mathbf{m}\right) d \mathbf{m}}{\int_{\Omega} \chi^{+}\left(\mathbf{v} \cdot \mathbf{m}\right) d \mathbf{m}} G1+(v)=∫Ωχ+(v⋅m)dm∫Ωχ+(v⋅m)G1(v,m)dm
结合 ( 13 ) \left(\mathrm{13}\right) (13)式:
cos θ o = G 1 + ( v ) ∫ Ω ⟨ m ⋅ v ⟩ D ( m ) d m \cos \theta_{o}=G_{1}^{+}\left(\mathbf{v}\right) \int_{\Omega}\left\langle\mathbf{m}\cdot \mathbf{v}\right\rangle D\left(\mathbf{m}\right) d \mathbf{m} cosθo=G1+(v)∫Ω⟨m⋅v⟩D(m)dm
所以:
G 1 + ( v ) = cos θ o ∫ Ω ⟨ v , m ⟩ D ( m ) d m G_{1}^{+}\left(\mathbf{v}\right)=\frac{\cos \theta_{o}}{\int_{\Omega}\left\langle\mathbf{v}, \mathbf{m}\right\rangle D\left(\mathbf{m}\right) d \mathbf{m}} G1+(v)=∫Ω⟨v,m⟩D(m)dmcosθo
但最后,因为对于背向 v \mathbf{v} v的那些面应该是不考虑的,所以我们还要引入阶跃函数:
(14) G 1 ( v , m ) = χ + ( v ⋅ m ) G 1 + ( v ) = χ + ( v ⋅ m ) cos θ o ∫ Ω ⟨ v ⋅ m ⟩ D ( m ) d m \begin{aligned} G_{1}\left(\mathbf{v}, \mathbf{m}\right)&=\chi^{+}\left(\mathbf{v} \cdot \mathbf{m}\right)G_{1}^{+}\left(\mathbf{v}\right) \\\\&=\chi^{+}\left(\mathbf{v} \cdot \mathbf{m}\right) \frac{\cos \theta_{o}}{\int_{\Omega}\left\langle\mathbf{v}\cdot \mathbf{m}\right\rangle D\left(\mathbf{m}\right) d \mathbf{m}} \end{aligned} \tag{14} G1(v,m)=χ+(v⋅m)G1+(v)=χ+(v⋅m)∫Ω⟨v⋅m⟩D(m)dmcosθo(14)
Smith遮挡函数:
对于很多PBR模型中(比如GGX和Beckmann)都会使用Smith遮挡函数。这个函数就是我们刚刚推导在 ( 14 ) \left(\mathrm{14}\right) (14)式的函数,只是我们把积分域从法向 v \mathbf{v} v换到了斜率空间 μ \mu μ了而已:
(15) G 1 ( v , m ) = χ + ( v ⋅ m ) 1 + Λ ( a ) G_{1}\left(\mathbf{v}, \mathbf{m}\right)=\frac{\chi^{+}\left(\mathbf{v} \cdot \mathbf{m}\right)}{1+\Lambda\left(a\right)}\tag{15} G1(v,m)=1+Λ(a)χ+(v⋅m)(15)
其中 a a a是向量 v \mathbf{v} v的斜率 μ = ∣ cot θ v ∣ \mu=\left|\cot \theta_{v}\right| μ=∣cotθv∣,而 Λ ( a ) \Lambda\left(a\right) Λ(a)5和式一样也是一个由 D ( m ) D\left(\mathbf{m}\right) D(m)决定的函数。(具体的推导过程篇幅很长,并且与我们理解概念没有多大关系,所以具体想了解可以可以参考有关推导6)
我们可以看到在式 ( 14 ) \left(\mathrm{14}\right) (14)和式 ( 15 ) \left(\mathrm{15}\right) (15),且在第三个假设的前提下是精确的(Exact)。
阴影遮挡函数:

微面不仅可能被遮挡(中图),还可能被阴影(左图),实际情况还会在微面中多次反射(右图)
回到 ( 6 ) \left(\mathrm{6}\right) (6)式,之前只考虑了遮挡情况。然而实际上除了在 v \mathbf{v} v方向微面有被遮挡的情况,在光射入的 l \mathbf{l} l方向也有微面在阴影中的情况,因此我们在实际使用的是阴影遮挡函数 G 2 G_2 G2。对于 G 2 G_2 G2函数在我们已经可以求得Smith遮挡函数的前提下,有以下几种模型:
阴影和遮挡函数不相关:
这是最早提出的,认为阴影和遮挡是不相关(independent)的,因此总会比实际微面被阴影/遮挡的值要大,会在渲染材质时显得更暗。
G 2 ( v , l , m ) = G 1 ( v , m ) G 1 ( l , m ) = χ + ( v ⋅ m ) 1 + Λ ( v ) χ + ( l ⋅ m ) 1 + Λ ( l ) \begin{aligned} G_{2}\left(\mathbf{v}, \mathbf{l}, \mathbf{m}\right) &=G_{1}\left(\mathbf{v}, \mathbf{m}\right) G_{1}\left(\mathbf{l}, \mathbf{m}\right) \\ &=\frac{\chi^{+}\left(\mathbf{v} \cdot \mathbf{m}\right)}{1+\Lambda\left(\mathbf{v}\right)} \frac{\chi^{+}\left(\mathbf{l} \cdot \mathbf{m}\right)}{1+\Lambda\left(\mathbf{l}\right)} \end{aligned} G2(v,l,m)=G1(v,m)G1(l,m)=1+Λ(v)χ+(v⋅m)1+Λ(l)χ+(l⋅m)
阴影遮挡函数是在微面高度上相关:
这个模型考虑了微面高度对阴影遮挡的相关性(correlation),高度越高的微面被遮挡/阴影或者同时被阴影遮挡的概率就越小,因此在近似精确度上已经远好于上一个模型了:
G 2 ( v , l , m ) = χ + ( v ⋅ m ) χ + ( l ⋅ m ) 1 + Λ ( v ) + Λ ( l ) G_{2}\left(\mathbf{v}, \mathbf{l}, \mathbf{m}\right)=\frac{\chi^{+}\left(\mathbf{v} \cdot \mathbf{m}\right) \chi^{+}\left(\mathbf{l} \cdot \mathbf{m}\right)}{1+\Lambda\left(\mathbf{v}\right)+\Lambda\left(\mathbf{l}\right)} G2(v,l,m)=1+Λ(v)+Λ(l)χ+(v⋅m)χ+(l⋅m)
阴影遮挡函数是在微面法向上相关:
这个模型考虑的是如果光线方向 l \mathbf{l} l和视线方向 v \mathbf{v} v夹脚越小的话,那么阴影和遮挡相关性就越高。在极限情况时,阴影/遮挡函数就完全相关了(full correlation)。
实际上在 l \mathbf{l} l和 v \mathbf{v} v的 a z i m u t h a l \mathrm{azimuthal} azimuthal角一致的情况下,阴影遮挡函数就是完全相关的。所以我们可以考虑把 a z i m u t h a l \mathrm{azimuthal} azimuthal角 ϕ \phi ϕ作为参数:
G 2 ( v , l , m ) = λ ( ϕ ) G 1 ( v , m ) G 1 ( l , m ) + ( 1 − λ ( ϕ ) ) min ( G 1 ( v , m ) , G 1 ( l , m ) ) \begin{array}{l}{G_{2}\left(\mathbf{v}, \mathbf{l}, \mathbf{m}\right)} \\ {=\lambda(\phi) G_{1}\left(\mathbf{v}, \mathbf{m}\right) G_{1}\left(\mathbf{l}, \mathbf{m}\right)+(1-\lambda(\phi)) \min \left(G_{1}\left(\mathbf{v}, \mathbf{m}\right), G_{1}\left(\mathbf{l}, \mathbf{m}\right)\right)}\end{array} G2(v,l,m)=λ(ϕ)G1(v,m)G1(l,m)+(1−λ(ϕ))min(G1(v,m),G1(l,m))
其中 λ ( ϕ ) \lambda(\phi) λ(ϕ)是一个经验函数,在下面会讲到
阴影遮挡函数在微面高度和法向上都是相关的:
同时考虑到两种相关性,因此也是最好的近似:
G 2 ( v , l , m ) = χ + ( v ⋅ m ) χ + ( l ⋅ m ) 1 + max ( Λ ( v ) , Λ ( l ) ) + λ ( v , l ) min ( Λ ( v ) , Λ ( l ) ) G_{2}\left(\mathbf{v}, \mathbf{l}, \mathbf{m}\right)=\frac{\chi^{+}\left(\mathbf{v} \cdot \mathbf{m}\right) \chi^{+}\left(\mathbf{l} \cdot \mathbf{m}\right)}{1+\max \left(\Lambda\left(\mathbf{v}\right), \Lambda\left(\mathbf{l}\right)\right)+\lambda\left(\mathbf{v}, \mathbf{l}\right) \min \left(\Lambda\left(\mathbf{v}\right), \Lambda\left(\mathbf{l}\right)\right)} G2(v,l,m)=1+max(Λ(v),Λ(l))+λ(v,l)min(Λ(v),Λ(l))χ+(v⋅m)χ+(l⋅m)
和仅高度相关的函数一样,也有一个关于 a z i m u t h a l \mathrm{azimuthal} azimuthal角的函数 λ ( ϕ ) \lambda(\phi) λ(ϕ),这个函数目前我们只能提供经验模型:
(16) λ = 4.41 ϕ 4.41 ϕ + 1 \lambda=\frac{4.41 \phi}{4.41 \phi+1} \tag{16} λ=4.41ϕ+14.41ϕ(16)
形状不变性与Roughness
对于一个渲染片元,我们想象将其拉伸(Stretching),如图:
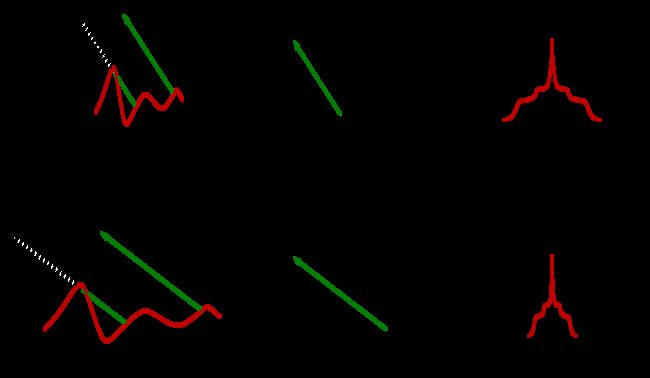
图中我们仅是一个一维空间的渲染片元。拉伸操作不会改变微面的拓扑结构,而且我们连观察向量 v \mathbf{v} v也一起拉伸的话,拉伸后阴影遮挡概率也是不变的。 然而对于微面的斜率分部函数,实际上是正好相反收缩的。如果微面的斜率分部改变了,相应地,法向概率分布函数 D ( m ) D(\mathbf{m}) D(m)也会改变。微面法向分布越集中就越光滑。这就是我们可以通过拉伸/收缩微面分部来控制渲染片元粗糙程度(Roughness)的原因!
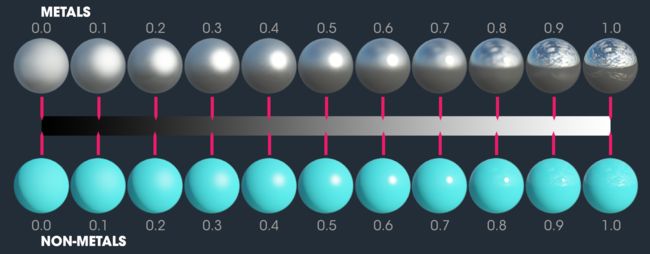
通过roughness/smoothness控制材质表面
因此我们定义粗糙程度参数为 α \alpha α,这个参数就是我们拉伸/收缩渲染片元的比例。从上面的图我们也能看出,对于观察方向 l \mathbf{l} l的斜率在此时和 α \alpha α的关系则为:
a = 1 α tan θ o a=\frac{1}{\alpha \tan \theta_{o}} a=αtanθo1
后面我们把只依赖粗糙程度 α \alpha α,而观察方向 a a a是由 α \alpha α决定的情况,定义为形状不变(shape invariant)
对于有形状不变假设的BRDF(比如:Beckmann,GGX)比起没有的(比如:Phong,GTR),有以下优势:
- 可以推导出各向异性的NDF和 G G G函数,用于渲染各项异性材质(关于各项异性材质渲染在后续文稿里再做介绍)。
- Smith G G G函数是建立在形状不变性假设上的,也因此只有形状不变的BRDF才有 G G G函数(关于NDF)的解析式,而像Phong模型是没有 G G G的解析式。
- 无论是 G G G还是NDF函数,只依赖唯一个变量 a a a,可查表求值(比如像Unity的内建shader就是这样做的),能提高运算效率。
基于PBR的BRDF
相信你能看到这里真的很了不起!一开始,我们从显微镜下观察到了物体的微面结构,然后做出了微面理论的三个假设,一步一步的用光学和几何学知识做为基础,推导出了基于微面理论的PBR模型。

在我们总结之前,需要完成我们高光项的最后形态,也就是把式中的遮挡函数 G 1 G_1 G1替换成式的 G 2 G_2 G2函数:
f ( l , v ) = F ( v , h ) G 2 ( v , h ) D ( h ) 4 ∣ n ⋅ v ∣ ∣ n ⋅ l ∣ f(\mathbf{l},\mathbf{v}) =\frac{F\left(\mathbf{v}, \mathbf{h}\right) G_{2}\left(\mathbf{v}, \mathbf{h}\right) D\left(\mathbf{h}\right)}{4\left|\mathbf{n} \cdot \mathbf{v}\right|\left|\mathbf{n} \cdot \mathbf{l}\right|} f(l,v)=4∣n⋅v∣∣n⋅l∣F(v,h)G2(v,h)D(h)
现在我们可以来总结前面的推导了:

迪士尼电影:无敌破坏王2,使用PBR渲染的主角
- PBR的BRDF和经典的BRDF一样,把渲染式分为高光项和漫反射项。
- 和经典BRDF一样,PBR把漫反射用一个兰伯特平面近似。
- 不同于经典BRDF,PBR把高光项用多个微小菲涅尔平面近似(即微面理论),使得高光项也同样具有物理意义。因此PBR是能量守恒的。
- PBR的高光项具有两个输入参数: F 0 F_0 F0表示材质的直接反光能力(通常在渲染器中也叫做Metallic),可参考上一篇。粗糙程度(Roughness) α \alpha α,用于调整物体表面光滑程度。在很多渲染引擎中会换算成高光度(Specular)和光泽度(Glossiness)两个参数

目前渲染器实现都支持roughness/metallical或者specular/glossiness
- 菲涅尔反射函数 F ( v , h ) F\left(\mathbf{v}, \mathbf{h}\right) F(v,h)项,通常用
F ( n , 1 ) ≈ F 0 + ( 1 − F 0 ) ( 1 − ( n ⋅ 1 ) + ) 5 F(\mathbf{n}, 1) \approx F_{0}+\left(1-F_{0}\right)\left(1-(\mathbf{n} \cdot 1)^{+}\right)^{5} F(n,1)≈F0+(1−F0)(1−(n⋅1)+)5
来近似,或者使用LUT查表求值。
- 分母项是用来归一化(normalized)的,和早期的Cook Torrence高光项很相似只是把 π \pi π换成了 4 4 4
- 法向面分布函数 D D D项表示关于法向的微面面积。对于不同的渲染材质(Material),有不同的 D D D函数。所以对于不同的材质,要么实际测量其微面分布,然后拟合其 D D D函数(比如皮肤),要么通过几何模型进行数学建模(比如布料)求出 D D D的解析式。

用几何建模实现的布料渲染
- 遮挡函数 G 1 G_1 G1项表示微面在观察方向被遮挡的概率。因为有2个自由度而且是和 D D D函数相关的,所以很难求出。而如果是用Smith遮挡函数,那么 G 1 G_1 G1函数不再依赖微面朝向,所以在已知 D D D函数的情况下可以直接解出。
- 实际模型中我们应该使用阴影遮挡函数 G 2 G_2 G2, G 2 G_2 G2是同时依赖观察者的遮挡和光线射入两个 G 1 G_1 G1函数的,而且 G 2 G_2 G2函数是会考虑两个 G 1 G_1 G1函数的相关性的。
- 如果 G 1 G_1 G1和 D D D只依赖粗糙程度 α \alpha α,而不依赖观察方向,那么BRDF是形状不变的。改变 α \alpha α不会改变微面的拓扑结构和阴影遮挡情况,也就不会改变材质的性质(Property)。
- PBR的BRDF也是没考虑子表面散射(Subsurface Scattering)的情况,所以也不能模拟折射(refraction)或透射(transmit)效果。

模拟子表面散射现象(图中红框所示)在PBR的模型下需要另外使用专门算法(ad-hoc)
BRDF基准测试
我们对于一个BRDF模型很重要的标准是:是否能量守恒。在考虑一个材质表面没有透射(因为BRDF无法模拟这种情况),同时也假设材料不吸收任何输入光时,能量是否守恒:
∫ Ω f ( l , v ) ∣ n ⋅ l ∣ d = 1 \int_{\Omega} f\left(\mathbf{l}, \mathbf{v}\right)\left|\mathbf{n} \cdot \mathbf{l}\right| d \mathbf=1 ∫Ωf(l,v)∣n⋅l∣d=1
这个测试叫做白炉测试(White Furnace Test),可以理解为一束照度(irrandiance)为 1 1 1的光从上往下照到材料表面(没有阴影):

光从法线方向照下来,没有投影的,所以不用考虑阴影情况
此时外面空间上有个光幕罩住了整个表面,我们要测试的就是整个光幕收集到的光照度和是否为 1 1 1:
白炉测试考虑所有反射出的光
但遗憾的是我们的微面模型BRDF并没有模拟蓝色向量中这种多次反射的现象(事实上是会被阴影遮挡函数 G 2 G_2 G2遮挡),所以是不可能通过白炉测试:

在被遮挡的情况下,白炉测试除了纯平的表面是不可能为1的
这也是理论上基于微面理论下的BRDF会比实际暗一点的原因。
但我们如果使用 G 1 G_1 G1函数,前面我们的推导就能表明:
∫ Ω ρ ( v , l ) ∣ n ⋅ l ∣ d l = ∫ Ω G 1 ( h , v ) D ( h ) 4 ∣ n ⋅ v ∣ d l = 1 \int_{\Omega} \rho\left(\mathbf{v}, \mathbf{l}\right)\left|\mathbf{n} \cdot \mathbf{l}\right| d \mathbf{l}=\int_{\Omega} \frac{G_{1}\left(\mathbf{h}, \mathbf{v}\right) D\left(\mathbf{h}\right)}{4\left|\mathbf{n} \cdot \mathbf{v}\right|} d \mathbf{l}=1 ∫Ωρ(v,l)∣n⋅l∣dl=∫Ω4∣n⋅v∣G1(h,v)D(h)dl=1
所以我们把能通过这种测试的BRDF模型称为弱白炉测试:
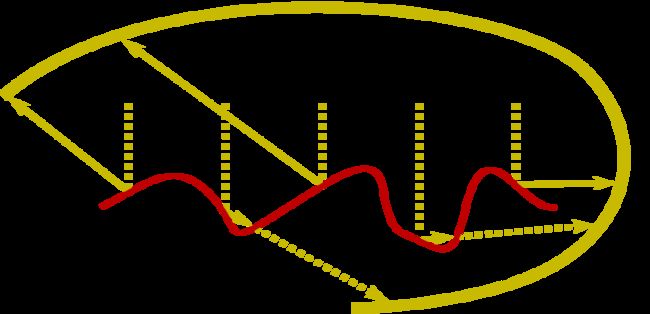
弱白炉测试,不再考虑遮挡情况
Smith遮挡函数的实用性
其实在历史上还存在另一个BRDF模型能通过弱白炉测试测试:V-cavity BRDF,最初的想法是通过若干不同尺度的V型表面来近似渲染材质:

用多个V形表面去模拟材质
而对于基于NDF的微面模型,自从G1函数被提出后很多年以后,我们才找出Smith遮挡函数,是的其通过弱白炉测试。
即使整个图形学历史上只有基于NDF的微面模型以及V-cavity模型是同时能证明通过弱白炉测试且在数学上精确的。但V-cavity模型由于不像微面模型依赖NDF分布函数,使得其实际渲染效果表现的非常糟糕,并没有什么实际的用处。
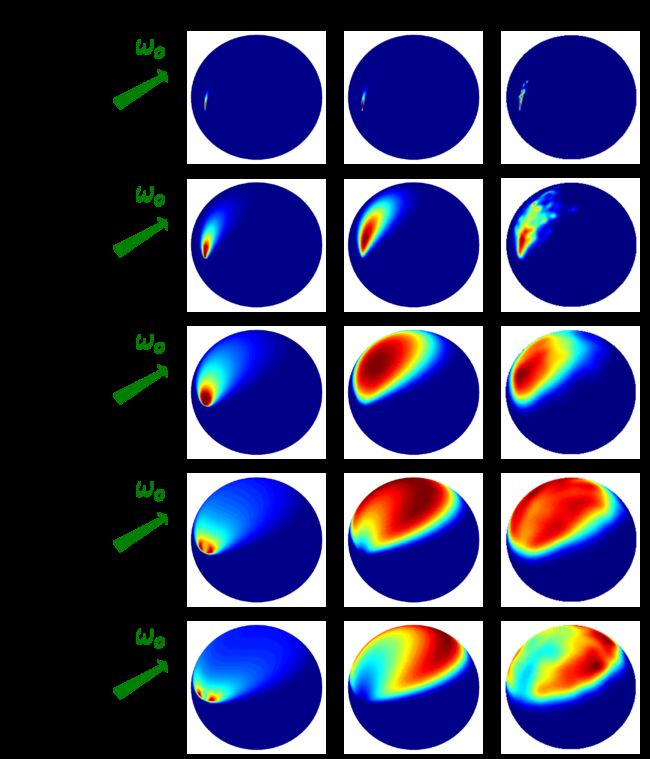
在不同的粗糙程度下,V-cavity模型(左列)的反射lobe比起Smith遮挡和NDF函数(中列)效果要差,参考蒙特卡洛光线跟踪算法(右列)
因此为什么在几乎所有的PBR渲染模型中(比如GGX)都使用Smith遮挡函数,就是因为其在假设的前提下是数学精确的且能量守恒的。而对于Smith遮挡函数的物理可行性和使用正态分布这两个优点都是我们推导过程中的副产品。
已实现的PBR
这里我们主要会介绍三种BRDF实现:Beckmann,Phong,GGX
Phong是基于经验模型开发的,Beckmann是在假设了高斯正态分布表面(gaussian rough surface)的前提下推导的模型,而GGX是目前使用最广泛的模型。Real Time Rendering 4th上也提到过GGX最初的提出者是Trowbridge and Reitz,只是后来被Disney公司命名为GGX,所以我们这里也特别提出来向原作者致敬!

电影:头号玩家
Beckmann:
D ( m ) = χ + ( m ⋅ n ) π α 2 cos 4 θ m exp ( − tan 2 θ m α 2 ) D\left(\mathbf{m}\right) =\frac{\chi^{+}\left(\mathbf{m} \cdot \mathbf{n}\right)}{\pi \alpha^{2} \cos ^{4} \theta_{m}} \exp \left(-\frac{\tan ^{2} \theta_{m}}{\alpha^{2}}\right) D(m)=πα2cos4θmχ+(m⋅n)exp(−α2tan2θm)
(17) Λ ( v ) = erf ( a ) − 1 2 + 1 2 a π exp ( − a 2 ) \Lambda\left(\mathbf{v}\right) =\frac{\operatorname{erf}(a)-1}{2}+\frac{1}{2 a \sqrt{\pi}} \exp \left(-a^{2}\right) \tag{17} Λ(v)=2erf(a)−1+2aπ1exp(−a2)(17)
其中
a = 1 α tan θ o a=\frac{1}{\alpha \tan \theta_{o}} a=αtanθo1
G 1 ( v , m ) = χ + ( v ⋅ m ) 1 + Λ ( v ) G_{1}\left(\mathbf{v}, \mathbf{m}\right)=\frac{\chi^{+}\left(\mathbf{v} \cdot \mathbf{m}\right)}{1+\Lambda\left(\mathbf{v}\right)} G1(v,m)=1+Λ(v)χ+(v⋅m)
对于 Λ ( v ) \Lambda\left(\mathbf{v}\right) Λ(v)会包含误差函数(error function),求值很麻烦,所以我们可以用如下公式近似:
(18) Λ ( v ) ≈ { 1 − 1.259 a + 0.396 a 2 3.533 a + 2.181 a 2 if a < 1.6 0 otherwise \Lambda\left(\mathbf{v}\right) \approx \left\{\begin{array}{ll}{\frac{1-1.259 a+0.396 a^{2}}{3.533 a+2.181 a^{2}}} & {\text { if } a<1.6} \\ {0} & {\text { otherwise }}\end{array}\right. \tag{18} Λ(v)≈{3.533a+2.181a21−1.259a+0.396a20 if a<1.6 otherwise (18)
GGX:
D ( m ) = χ + ( m ⋅ n ) π α 2 cos 4 θ m ( 1 + tan 2 θ m α 2 ) 2 Λ ( v ) = − 1 + 1 + 1 a 2 2 \begin{aligned} D\left(\mathbf{m}\right) &=\frac{\chi^{+}\left(\mathbf{m} \cdot \mathbf{n}\right)}{\pi \alpha^{2} \cos ^{4} \theta_{m}\left(1+\frac{\tan ^{2} \theta_{m}}{\alpha^{2}}\right)^{2}} \\ \Lambda\left(\mathbf{v}\right) &=\frac{-1+\sqrt{1+\frac{1}{a^{2}}}}{2} \end{aligned} D(m)Λ(v)=πα2cos4θm(1+α2tan2θm)2χ+(m⋅n)=2−1+1+a21
其中
a = 1 α tan θ o a=\frac{1}{\alpha \tan \theta_{o}} a=αtanθo1
以及
G 1 ( v , m ) = χ + ( v ⋅ m ) 1 + Λ ( v ) G_{1}\left(\mathbf{v}, \mathbf{m}\right)=\frac{\chi^{+}\left(\mathbf{v} \cdot \mathbf{m}\right)}{1+\Lambda\left(\mathbf{v}\right)} G1(v,m)=1+Λ(v)χ+(v⋅m)
Phong/Blinn:
由于Phong在计算机渲染领域曾经是最重要的模型,虽然现在已经差不多抛弃了,但我们还是给出Phong模型在PBR下的式子:
D ( m ) = χ + ( n ⋅ m ) α p + 2 2 π ( n ⋅ m ) α p D(\mathbf{m})=\chi^{+}(\mathbf{n} \cdot \mathbf{m}) \frac{\alpha_{p}+2}{2 \pi}(\mathbf{n} \cdot \mathbf{m})^{\alpha_{p}} D(m)=χ+(n⋅m)2παp+2(n⋅m)αp
为了使得粗糙程度参数调整上比较均匀,我们用 α b \alpha_b αb控制粗糙程度,因此和 α p \alpha_p αp的关系是:
α p = 2 α b − 2 − 2 \alpha_{p}=2 \alpha_{b}^{-2}-2 αp=2αb−2−2
然而在PBR下的Phong模型是有一些缺陷的:一是Phong不是形状不变的,所以在调整粗糙程度时会改变微面分布情况。而另一个是 Λ ( v ) \Lambda\left(\mathbf{v}\right) Λ(v)没有解析式,我们可以令 a = 0.5 α p + 1 / ( tan θ o ) a=\sqrt{0.5 \alpha_{p}+1} /\left(\tan \theta_{o}\right) a=0.5αp+1/(tanθo),然后用Beckmann( ( 17 ) \left(\mathrm{17}\right) (17)式或 ( 18 ) \left(\mathrm{18}\right) (18)式)代替。这时Phong和Beckmann模型的表现是非常接近的

在和反射向量呈不同角度高光光线密度,上图中蓝色虚线是Phong/Blinn模型,绿色实线是Beckmann模型,红色实线是GGX模型
下图中,上行是Phong和Beckmann模型的渲染效果,下行是GGX的渲染效果,可以看出GGX渲染高光处出现了"光晕"
PBR模型评价:
现在我们来考察这几种模型在微面分布 D D D上的区别。对于Phong和Beckmann其微面分布是基本一致的,所以渲染结果基本也一致。而对于GGX,对比起Beckmann来,分布图上会多出了一条“尾巴“,这使得GGX在实际渲染高光时是随着粗糙程度增加而呈现光晕效果的。
究竟哪个模型更好,由于篇幅,我们在这里只给出结论:GGX更接近现实的情况。

GGX模型和Phong/Blinn模型的比较
所以由于GGX模型在计算量和近似程度上都当之无愧是目前使用范围最广的模型。
PBR之后

使用Blender渲染引擎渲染,图片来自艺术家Daniel Bystedt
终于,不辞千辛万苦,我们算是彻底的理解了PBR是如何工作的!
在讨论完PBR,去大干一场之前我们再来看看目前PBR的一些发展方向:

左为真实情况时的NDF表面,右为PBR模型下的NDF表面
- 能否在不做出第三个假设前提下,推导出一个类似Smith遮挡函数的方案。因为实际中,微面都是自相关(autocorrect)的,而Smith遮挡函数的近似就会过于理想。
- 对于Smith遮挡函数的闭解析式目前只找到了Beckmann和GGX的,而对于更好的GGX的泛化模型GTR还没有找到,这使得GTR模型无法得到有效使用。
- 对于遮挡阴影函数 ( 16 ) \left(\mathrm{16}\right) (16)式,我们还只能使用经验模型,对于推导出数学精确模型一直都受到关注。

Pixar的RenderMan实现的SpecRough Lobe
- 能否在介于完全镜面反射的高光项和完全漫反射的漫反射项之间再创造出一个额外的高光反射项(specular lobe),以解决目前过于复杂的PBR模型推导。
最后我也真诚的建议你去阅读一下这几年SIGGRAPH的重头戏,有关PBR的一些应用或研究:
https://blog.selfshadow.com/publications/s2017-shading-course/
作者后记
这是我第一篇真正完成的技术系列,前后做了很多尝试都未能满意,绞尽脑汁完成后又觉得意犹未尽。突然间想起了安静的躺在加州博物馆里的这只犹他茶壶(相信如果从事图形学工作的人一定不会陌生吧)。

收藏在计算机历史博物馆里犹他茶壶
谁能想到这只普通的不得了的茶壶却是如今这个充满想象的虚拟世界的开端。作为一名独立研究者,独立游戏制作者,除了平时默默耕耘外,也希望在喜欢的事情上开个好头!也欢迎和我一样喜欢研究技术,或者对艺术热爱的你,疯狂的骚扰我吧!

goolyuyi,微博:@goolyuyi
Real Time Rendering 4th第9章:Physically Based Shading主要是介绍了PBR的BRDF的结论 ↩︎
渲染片元,这里理解为要渲染某个物体表明上的一小块,在实时渲染中对应于屏幕上一块像素的渲染 ↩︎
在光学的描述使用辉度(光辉)更为准确,而不是使用辐射学的辐照度 ↩︎ ↩︎
虽然Phong模型也有微面理论的假设,但仍然是一个经验模型 ↩︎
这里要特别申明一下,后面的数学公式为了书写方便,其中即使 Λ \Lambda Λ函数输入的是一个向量,比如 Λ ( v ) \Lambda(\mathbf{v}) Λ(v),也表示输入的是该向量的斜率,即 Λ ( cot ( θ o ) ) \Lambda(\cot({\theta_{o}})) Λ(cot(θo))。 ↩︎
Trowbridge, T. S., and K. P. Reitz, “Average Irregularity Representation of a Roughened Surface for Ray Reflection,”Appendix A ↩︎