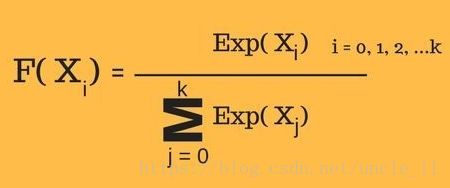详解sigmoid与softmax， 多分类及多标签分类

激活函数介绍

对于熟悉机器学习或神经网络的读者来说，sigmoid与softmax两个激活函数并不陌生，但这两个激活函数在逻辑回归中应用，也是面试和笔试会问到的一些内容，掌握好这两个激活函数及其衍生的能力是很基础且重要的，下面为大家介绍下这两类激活函数。

sigmoid激活函数

从函数定义上来看，sigmoid激活函数的定义域能够取任何范围的实数，而返回的输出值在0到1的范围内。sigmoid函数也被称为S型函数，这是由于其函数曲线类似于S型，在下面的内容中可以看到。此外，该函数曲线也可以用于统计中，使用的是累积分布函数。

sigmoid激活函数的性质

根据定义，sigmoid激活函数的计算公式如下：

其中:

• x: 输入
• float：表示浮点型数据
• exp：对其求指数
• f(x): 函数输出

从上述函数可以看到，x的取值范围可以是全实数，sigmoid函数返回一个实数值输出，此外，sigmoid函数的一阶导数是非负或非正：

• 非负： 如果输入数字大于或等于零；
• 非正： 如果输入数字小于或等于零；

sigmoid激活函数的使用

• Sigmoid函数用于逻辑回归模型中的二进制分类。
• 在创建人造神经元时，Sigmoid函数用作激活函数。
• 在统计学中，S形函数图像是常见的累积分布函数。

sigmoid激活函数python实现并画图

实现代码

# Required Python Package
import numpy as np

def sigmoid(inputs):
    """
    Calculate the sigmoid for the give inputs (array)
    :param inputs:
    :return:
    """
    sigmoid_scores = [1 / float(1 + np.exp(- x)) for x in inputs]
    return sigmoid_scores


sigmoid_inputs = [2, 3, 5, 6]
print "Sigmoid Function Output :: {}".format(sigmoid(sigmoid_inputs))

上是Sigmoid函数的实现代码。该函数将以列表形式的值作为输入参数。列表中的每个元素值将被视为Sigmoid函数的输入，并计算输出值。
接下来，我们将一个列表sigmiod_inputs作为函数的输入，列表值为2,3,5,6，经过sigmoid函数计算后获得Sigmoid分数。
函数输出：

Sigmoid Function Output :: [0.8807970779778823, 0.9525741268224334, 0.9933071490757153, 0.9975273768433653]

画图

现在使用上面的函数来创建图像，以方便了解Sigmoid函数的性质。传递一个包含0到21范围内的数字的列表，计算输入列表的sigmoid分数，然后使用输出值来显示图像。

# Required Python Packages
import numpy as np
import matplotlib.pyplot as plt


def sigmoid(inputs):
    """
    Calculate the sigmoid for the give inputs (array)
    :param inputs:
    :return:
    """
    sigmoid_scores = [1 / float(1 + np.exp(- x)) for x in inputs]
    return sigmoid_scores


def line_graph(x, y, x_title, y_title):
    """
    Draw line graph with x and y values
    :param x:
    :param y:
    :param x_title:
    :param y_title:
    :return:
    """
    plt.plot(x, y)
    plt.xlabel(x_title)
    plt.ylabel(y_title)
    plt.show()


graph_x = range(0, 21)
graph_y = sigmoid(graph_x)

print "Graph X readings: {}".format(graph_x)
print "Graph Y readings: {}".format(graph_y)

line_graph(graph_x, graph_y, "Inputs", "Sigmoid Scores")

创建一个包含0到21范围内的数字的graph_x列表，之后在graph_y列表中存储给定graph_x输入的计算sigmoid分数，调用line_graph函数，该函数采用图像的x，y和标题来创建线形图。
脚本输出：

Graph X readings: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]

Graph Y readings: [0.5, 0.7310585786300049, 0.8807970779778823, 0.9525741268224334, 0.9820137900379085, 0.9933071490757153, 0.9975273768433653, 0.9990889488055994, 0.9996646498695336, 0.9998766054240137, 0.9999546021312976, 0.999983298578152, 0.9999938558253978, 0.999997739675702, 0.9999991684719722, 0.999999694097773, 0.9999998874648379, 0.9999999586006244, 0.9999999847700205, 0.9999999943972036, 0.9999999979388463]

从上图可以看出，随着输入值的增加，sigmoid得分增加到1。

softmax激活函数

Softmax函数计算事件超过’n’个不同事件的概率分布。一般来说，这个函数将会计算每个目标类别在所有可能的目标类中的概率。计算出的概率将有助于确定给定输入的目标类别。
使用Softmax的主要优点是输出概率的范围，范围为0到1，所有概率的和将等于1。如果将softmax函数用于多分类模型，它会返回每个类别的概率，并且目标类别的概率值会很大。指数公式计算给定输入值的指数和输入中所有值的指数值之和。那么输入值的指数与指数值之和的比值就是softmax函数的输出。

softmax激活函数的性质

根据定义，softmax激活函数的计算公式如下：

其中:

• x: 输入
• exp：对其求指数
• f(x): 函数输出
  从上述计算公式可以看出：
• 计算出的概率将在0到1的范围内。
• 所有概率的和等于1。

softmax激活函数的使用

• 用于多重分类逻辑回归模型。
• 在构建神经网络中，在不同的层使用softmax函数。

softmax激活函数python实现并画图

实现代码

# Required Python Package
import numpy as np


def softmax(inputs):
    """
    Calculate the softmax for the give inputs (array)
    :param inputs:
    :return:
    """
    return np.exp(inputs) / float(sum(np.exp(inputs)))


softmax_inputs = [2, 3, 5, 6]
print "Softmax Function Output :: {}".format(softmax(softmax_inputs))

脚本输出:

Softmax Function Output :: [ 0.01275478  0.03467109  0.25618664  0.69638749]

从中可以观察到，输入值为6时，函数输出值的概率最高，这是可以从softmax函数预先知道的。之后在分类任务中，可以使用高概率值来预测给定输入特征的目标类别。

画图

现在让我们使用实现的Softmax函数创建图像来了解这个函数的表现。
创建一个包含0到21范围内的值的列表，之后将通过此列表来计算已实现函数的分数，使用列表和估计分数创建图像。

# Required Python Packages
import numpy as np
import matplotlib.pyplot as plt


def softmax(inputs):
    """
    Calculate the softmax for the give inputs (array)
    :param inputs:
    :return:
    """
    return np.exp(inputs) / float(sum(np.exp(inputs)))


def line_graph(x, y, x_title, y_title):
    """
    Draw line graph with x and y values
    :param x:
    :param y:
    :param x_title:
    :param y_title:
    :return:
    """
    plt.plot(x, y)
    plt.xlabel(x_title)
    plt.ylabel(y_title)
    plt.show()


graph_x = range(0, 21)
graph_y = softmax(graph_x)

print "Graph X readings: {}".format(graph_x)
print "Graph Y readings: {}".format(graph_y)

line_graph(graph_x, graph_y, "Inputs", "Softmax Scores")

脚本输出：

Graph X readings: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
Graph Y readings: [ 1.30289758e-09 3.54164282e-09 9.62718331e-09 2.61693975e-08 7.11357976e-08 1.93367146e-07 5.25626399e-07 1.42880069e-06 3.88388295e-06 1.05574884e-05 2.86982290e-05 7.80098744e-05 2.12052824e-04 5.76419338e-04 1.56687021e-03 4.25919483e-03 1.15776919e-02 3.14714295e-02 8.55482149e-02 2.32544158e-01 6.32120559e-01]

该图显示了softmax函数的基本属性，输入值越大，其概率越高。

多类分类及多标签分类

多类分类意味着候选集是一个多分类，而不仅仅是二分类，不是是与否的问题，而是属于多类中哪一类的问题。一个样本属于且只属于多个分类中的一个，一个样本只能属于一个类，不同类之间是互斥的。举例而言，MNIST数据集，常用的数字手写体识别数据集，它的标签是一个多分类的过程，要将数字手写体识别为0~9中的某一个数字：

而对于多标签分类而言，一个样本的标签不仅仅局限于一个类别，可以具有多个类别，不同类之间是有关联的。比如一件衣服，其具有的特征类别有长袖、蕾丝等属性等，这两个属性标签不是互斥的，而是有关联的。

使用softmax和sigmoid激活函数来做多类分类和多标签分类

在实际应用中，一般将softmax用于多类分类的使用之中，而将sigmoid用于多标签分类之中，对于图像处理而言，网络模型抽取图像特征的结构基本相同，只是根据不同的任务改变全连接层后的输出层。下面介绍如何使用softmax和sigmoid完成对应的分类任务。

softmax激活函数应用于多类分类

假设神经网络模型的最后一层的全连接层输出的是一维向量logits=[1,2,3,4,5,6,7,8,9,10],这里假设总共类别数量为10，使用softmax分类器完成多类分类问题，并将损失函数设置为categorical_crossentropy损失函数：
用tensorflow实现：

tf.argmax(tf.softmax(logits))

首先用softmax将logits转换成一个概率分布，然后取概率值最大的作为样本的分类 。softmax的主要作用其实是在计算交叉熵上，将logits转换成一个概率分布后再来计算，然后取概率分布中最大的作为最终的分类结果，这就是将softmax激活函数应用于多分类中。

sigmoid激活函数应用于多标签分类

sigmoid一般不用来做多类分类，而是用来做二分类，它是将一个标量数字转换到[0,1]之间，如果大于一个概率阈值(一般是0.5)，则认为属于某个类别，否则不属于某个类别。这一属性使得其适合应用于多标签分类之中，在多标签分类中，大多使用binary_crossentropy损失函数。它是将一个标量数字转换到[0,1]之间，如果大于一个概率阈值(一般是0.5)，则认为属于某个类别。本质上其实就是针对logits中每个分类计算的结果分别作用一个sigmoid分类器，分别判定样本是否属于某个类别同样假设，神经网络模型最后的输出是这样一个向量logits=[1,2,3,4,5,6,7,8,9,10], 就是神经网络最终的全连接的输出。这里假设总共有10个分类。通过：

tf.sigmoid(logits)

sigmoid应该会将logits中每个数字都变成[0,1]之间的概率值，假设结果为[0.01, 0.05, 0.4, 0.6, 0.3, 0.1, 0.5, 0.4, 0.06, 0.8], 然后设置一个概率阈值，比如0.3，如果概率值大于0.3，则判定类别符合，那么该输入样本则会被判定为类别3、类别4、类别5、类别7及类别8。即一个样本具有多个标签。
在这里强调一点：将sigmoid激活函数应用于多标签分类时，其损失函数应设置为binary_crossentropy。