STL源码分析(总结)
STL六大组件
- 容器(containers):是一种class template,里面包含各种数据结构。
- 算法(algorithms):是一种function template,里面包含各种算法。
- 迭代器(iterators):是所谓的泛型指针,每个容器都有自己的专属的迭代器,知道如何遍历自己的元素。
- 仿函数(functors):是一种重载了operator()的class或class template,可作为算法的某种策略。
- 配接器(adapters):是一种用来修饰容器或仿函数或迭代器接口的东西。
- 配置器(allocators):是一个实现了动态空间配置,空间管理,空间释放的class template,负责空间配置与管理。
空间配置器
构造
- 分配新的空间
- 在新空间上构造对象
template T>
inline T* _allocate(...) {
...
T* tmp = (T*)(::operate new((size_t)(size * sizeof(T))));
...
} template <class T1, class T2>
inline void _construct(T1* p, const T2& value) {
new(p) T1(value); //placement new.
}operator new
(1)只分配所要求的空间,不调用相关对象的构造函数。当无法满足所要求分配的空间时,则
->如果有new_handler,则调用new_handler,否则
->如果没要求不抛出异常(以nothrow参数表达),则执行bad_alloc异常,否则
->返回0
(2)可以被重载
(3)重载时,返回类型必须声明为void*
(4)重载时,第一个参数类型必须为表达要求分配空间的大小(字节),类型为size_t
(5)重载时,可以带其它参数
Placement new
placement new 是重载operator new 的一个标准、全局的版本,它不能够被自定义的版本代替(不像普通版本的operator new和operator delete能够被替换)。
对象的分配
在已分配的缓存区调用placement new来构造一个对象。
Task *ptask = new (buf) Task
SGI中的空间配置与释放(std::alloc)
SGI设计哲学:
- 向system heap要求空间
- 考虑多线程状态
- 考虑内存不足时的应变措施
- 考虑过多“小型区块”可能造成的碎片问题
内存分配中使用::operator new()与::operator delete()分配与释放相当于molloc()与free().
考虑第四点设计了双层配置器,第一层直接调用malloc()和free().
配置内存小于128bytes时,使用第二级配置器:
使用16个自由链表负责16种小型区块的次级配置能力。如果内存不足转一级配置器。
8 16 24 32 40 48 56 64 72 80 88 96 104 112 120 128
迭代器
迭代器类似于一种智能指针,比较重要的行为有内容提领和成员访问。
迭代器相应型别
为了让迭代器适应不同种类的容器即泛化,需利用function template的参数推导机制推导型别。
偏特化:如果class template拥有一个以上的template参数,我们可以针对其中某个template参数进行特化工作(我们可以在泛化设计中提供一个特化版本)。
trans编程技法
声明内嵌型别推导函数返回值:
template <class T>
struct MyIter {
typedef T value_type; //内嵌型别
T* ptr;
MyIter(T* p=0) : ptr(p) {}
T& operator*() const { return *ptr; }
//...
}
template <class I>
typename I::value_type //这一整行是func的返回值型别
func(I ite) {
return *ite;
}
MyIter<int> ite(new int(8));
cout << func(ite);萃取型别:
template <class I>
struct iterator_traits {
typedef typename I::value_type value_type;
}
template <class I>
typename iterator_traits::value_type //函数返回型别
func(I ite) {
return *ite;
}
//萃取原生指针,偏特化版本
template <class T>
struct iterator_traits {
typedef T value_type;
}; STL根据经验,定义了迭代器最常用到的五种类型:value_type、difference_type、pointer、reference、iterator_category,任何开发者如果想将自己开发的容器与STL结合在一起,就一定要为自己开发的容器的迭代器定义这五种类型,这样都可以通过统一接口iterator_traits萃取出相应的类型,下面列出STL中iterator_traits的完整定义:
tempalte<typename I>
struct iterator_traits
{
typedef typename I::iterator_category iterator_category;
typedef typename I::value_type value_type;
typedef typeanme I:difference_type difference_type;
typedef typename I::pointer pointer;
typedef typename I::reference reference;
};重点提一下iterator_category:
根据移动特性与施行操作,迭代器被分为五类:
- Input Iterator:只读
- Output Iterator:只写
- Forward Iterator:允许“写入型”算法(例如replace())在此种迭代器所形成的区间上进行读写操作。
- Bidirectional Iterator:可双向移动。
- Random Access Iterator:前四种迭代器都只供应一部分指针算术能力(前三种支持 operator++,第四种再加上operator–),第五种则涵盖所有指针算术能力,包括p+n, p-n, p[n], p1-p2, p1
序列式容器
vector
vector底层为动态数组,分配策略为:
- 如果vector原大小为0,则配置1,也即一个元素的大小。
- 如果原大小不为0,则配置原大小的两倍。
当然,vector的每种实现都可以自由地选择自己的内存分配策略,分配多少内存取决于其实现方式,不同的库采用不同的分配策略。
当以两倍空间增长时之前分配的内存空间不可能被使用,这样对于缓存并不友好。
相关连接:https://www.zhihu.com/question/36538542
vector的迭代器
使用vector迭代器时要时刻注意vector是否发生了扩容,一旦扩容引起了空间重新配置,指向原vector的所有迭代器都将失效。
vector维护的是一个连续线性空间,与数组array一样,所以无论其元素型别为何,普通指针都可以作为vector的迭代器而满足所有必要的条件。vector所需要的迭代器操作,包括operator*,operator->,operator++,operator–,operator+=,operator-=等,普通指针都具有。
vector提供了Random Access Iterators。
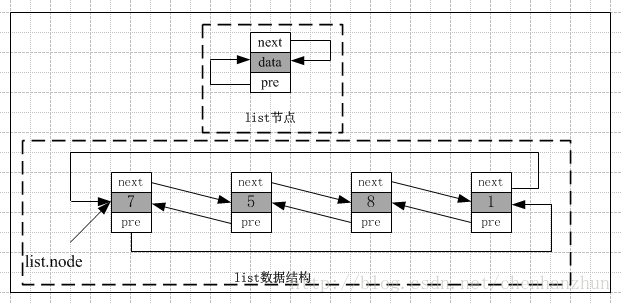
list
list容器完成的功能实际上和数据结构中的双向链表是极其相似的,list中的数据元素是通过链表指针串连成逻辑意义上的线性表
对于迭代器,只能通过“++”或“–”操作将迭代器移动到后继/前驱节点元素处,而不能对迭代器进行+n或-n的操作。增加任何元素都不会使迭代器失效。删除元素时,除了指向当前被删除元素的迭代器外,其它迭代器都不会失效。
deque
**deque是一种双向开口的线性空间。**deque容器类与vector类似,支持随机访问和快速插入删除,它在容器中某一位置上的操作所花费的是线性时间。虽然vector也支持从头端插入元素,不过效率奇差,deque与vector最大差异:
- deque允许常数时间内对起头端进行元素的插入或移除操作。
- deque没有所谓的容量观念,因为它是动态的以分段连续空间组合而成,随时可以增加一段新的空间并拼接起来。
![]()
一旦有必要在deque的前段或尾端增加新空间,便配置一段定量连续空间,串在整个deque的头端或尾端。迭代器较为复杂,操作复杂度大。
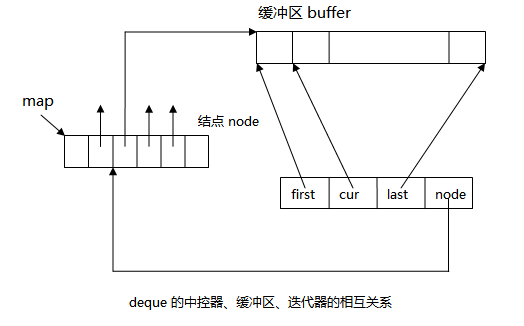
deque是由一块所谓的map作为主控,map是一段连续的空间,其中每个元素指向另一段连续的空间,称为缓冲区。一旦map空间不足,需配备一块更大的map。
deque迭代器
虽然deque也提供Random Access Iterators,不过其迭代器比较特殊。
迭代器失效:
插入操作:
1、在队前或队后插入元素时(push_back(),push_front()),由于可能缓冲区的空间不够,需要增加map中控器,而中控器的个数也不够,所以新开辟更大的空间来容纳中控器,所以可能会使迭代器失效;但指针、引用仍有效,因为缓冲区已有的元素没有重新分配内存。
2、在队列其他位置插入元素时,由于会造成缓冲区的一些元素的移动(源码中执行copy()来移动数据),所以肯定会造成迭代器的失效;并且指针、引用都会失效。
删除操作:
1、删除队头或队尾的元素时,由于只是对当前的元素进行操作,所以其他元素的迭代器不会受到影响,所以一定不会失效,而且指针和引用也都不会失效;
2、删除其他位置的元素时,也会造成元素的移动,所以其他元素的迭代器、指针和引用都会失效。
stack
是一种配接器,将接口改变符合先进后出规则,没有迭代器。
以deque为底层容器,以list为底层容器。
queue
是一种配接器,将接口改变符合先进先出规则,没有迭代器。
以deque为底层容器,以list为底层容器。
priority_queue
是一种配接器,没有迭代器,是以二叉堆为底层数据结构来实现的,所以先简单介绍heap。
heap
堆的实现通过构造二叉堆(binary heap),实为二叉树的一种;由于其应用的普遍性,当不加限定时,均指该数据结构的这种实现。这种数据结构具有以下性质。
- 任意节点小于(或大于)它的所有后裔,最小元(或最大元)在堆的根上(堆序性)。
- 堆总是一棵完全树。即除了最底层,其他层的节点都被元素填满,且最底层尽可能地从左到右填入。
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆,STL供应的是最大堆。
在SGI STL中用array来实现堆,则当某个节点位于i处时,其左子节点和右子节点分别为2i,2i+1,父节点为i/2.
priority_queue 优先级队列是一个拥有权值概念的单向队列queue,在这个队列中,所有元素是按优先级排列的(也可以认为queue是个按进入队列的先后做为优先级的优先级队列——先进入队列的元素优先权要高于后进入队列的元素)。
priority_queue默认使用vector作为底层容器,默认会在构造时通过max-heap建堆。
关联式容器
标准的STL关联式容器分为set(集合)/map(映射表)两大类,以及这两大类的衍生体multiset(多键集合)和 multimap(多键映射表)。这些容器的底层机制均以RB-tree(红黑树)完成。RB-tree也是一个独立容器,但并不开放给外界使用。
此外,SGI STL 还提供了一个不在标准规格之列的关联式容器:hash table (散列表),以及以此hash table 为底层机制而完成的hash_set(散列集合)、hash_map(散列映射表)、hash_multiset(散列多键集合)、hash_multimap(散列多键映射表)。
根据C++ 11标准的推荐,用unordered_map代替hash_map。
所谓的关联式容器,观念上类似关联式数据库:每笔数据(每个元素)都有一个键值(key)和一个实值(value)。当元素被插入到关联式容器中时,容器内部结构(可能是RB-tree ,也可能是hash-table)便依照其键值大小,以某种特定规则将这个元素放置于适当位置。关联式容器没有所谓的头尾(只有最大元素和最小元素),所以不会有所谓push_back()/push_front()/pop_back()/pop_front()/begin()/end() 这样的操作行为。
一般而言,关联式容器的内部结构是一个balanced binary tree(平衡二叉树),以便获得良好的搜寻效率。balanced binary tree 有许多种类型,包括AVL-tree、RB-tree、AA-tree ,其中最被广泛运用于STL的是RB-tree(红黑树)。
红黑树
算法导论对R-B Tree的介绍:
红黑树,一种二叉查找树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。
通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
红黑树的5个性质:
- 每个结点要么是红的要么是黑的。
- 根结点是黑的。
- 每个叶结点(叶结点即指树尾端NIL指针或NULL结点)都是黑的。
- 如果一个结点是红的,那么它的两个儿子都是黑的。
- 对于任意结点而言,其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点。
红黑树能够以O(log2 n) 的时间复杂度进行搜索、插入、删除操作。此外,由于它的设计,任何不平衡都会在三次旋转之内解决。当然,还有一些更好的,但实现起来更复杂的数据结构,能够做到一步旋转之内达到平衡,但红黑树能够给我们一个比较“便宜”的解决方案。红黑树的算法时间复杂度和AVL相同,但统计性能比AVL树更高。
红黑树节点和迭代器:
红黑树节点和迭代器的设计和slist原理一样,将结构和数据分离.原理如下:
struct __rb_tree_node_base
{
typedef __rb_tree_color_type color_type;
typedef __rb_tree_node_base* base_ptr;
color_type color; // 红黑树的颜色
base_ptr parent; // 父节点
base_ptr left; // 指左节点
base_ptr right; // 指向右节点
}
template <class Value>
struct __rb_tree_node : public __rb_tree_node_base
{
typedef __rb_tree_node* link_type;
Value value_field; // 存储数据
}; 红黑树的基础迭代器为struct __rb_tree_base_iterator,主要成员就是一个__rb_tree_node_base节点,指向树中某个节点,作为迭代器与树的连接关系,还有两个方法,用于将当前迭代器指向前一个节点decrement()和下一个节点increment().下面看下正式迭代器的源码:
template <class Value, class Ref, class Ptr>
struct __rb_tree_iterator : public __rb_tree_base_iterator
{
typedef Value value_type;
typedef Ref reference;
typedef Ptr pointer;
typedef __rb_tree_iterator iterator;
typedef __rb_tree_iteratorconst Value&, const Value*> const_iterator;
typedef __rb_tree_iterator self;
typedef __rb_tree_node* link_type;
__rb_tree_iterator() {}//迭代器默认构造函数
__rb_tree_iterator(link_type x) { node = x; }//由一个节点来初始化迭代器
__rb_tree_iterator(const iterator& it) { node = it.node; }//迭代器复制构造函数
//迭代器解引用,即返回这个节点存储的数值
reference operator*() const { return link_type(node)->value_field; }
#ifndef __SGI_STL_NO_ARROW_OPERATOR
//返回这个节点数值值域的指针
pointer operator->() const { return &(operator*()); }
#endif /* __SGI_STL_NO_ARROW_OPERATOR */
//迭代器++运算
self& operator++() { increment(); return *this; }
self operator++(int) {
self tmp = *this;
increment();
return tmp;
}
//迭代器--运算
self& operator--() { decrement(); return *this; }
self operator--(int) {
self tmp = *this;
decrement();
return tmp;
}
};
inline bool operator==(const __rb_tree_base_iterator& x,
const __rb_tree_base_iterator& y) {
return x.node == y.node;
// 两个迭代器相等,指这两个迭代器指向的节点相等
}
inline bool operator!=(const __rb_tree_base_iterator& x,
const __rb_tree_base_iterator& y) {
return x.node != y.node;
// 两个节点不相等,指这两个迭代器指向的节点不等
} 迭代器的解引用运算,返回的是这个节点的值域.所以对于set来说,返回的就是set存储的值,对于map来说,返回的就是pair
size_type node_count; // 记录树的大小(节点的个数)
link_type header;
Compare key_compare; // 节点间的比较器,是仿函数对于header,其实相当与链表中的头节点,不存储数据,可用于红黑树的入口.header的设计可以说的STL红黑树设计的一个亮点,header和root互为父节点,header的左节点指向最小的值,header的右节点指向最大的值,所以header也可以作为end()迭代器指向的值.图示如下:
红黑树的操作就不再赘述,算法书里都有介绍。
map&set
map底层用的是红黑树,所以map只是在红黑树上加了一层封装,set同理。
multiset与multimap与上述最大的不同在于允许重复的键值在红黑树上,插入操作采用的是底层RB-Tree的insert_equal()而非insert_unique()。
迭代器失效:如果迭代器所指向的元素被删除,则该迭代器失效。其它任何增加、删除元素的操作都不会使迭代器失效。
hashtable
hashtable即所谓的散列表,对于冲突的解决方法,stl采用开链的方法来解决冲突。STL的做法是在bucket中维护一个list,然后key对应的值插入list。至于buckets聚合体,stl采用vector作为底层容器。
hash_table节点的定义:
template <class _Val>
struct _Hashtable_node
{
_Hashtable_node* _M_next;
_Val _M_val;
};hashtable的迭代器:
struct _Hashtable_iterator {
typedef _Hashtable_node<_Val> _Node;
typedef forward_iterator_tag iterator_category;
_Node* _M_cur;
_Hashtable* _M_ht;
iterator& operator++();
iterator operator++(int);
};hashtable的迭代器类型为ForwardIterator,所以只支持operator++操作。
hashtable关键实现:
对于散列表大小的选取,CLRS上面也提到了m常常选择与2的幂不太接近的质数。在这种情况下,取一个素数总是个不坏的选择。
SGI STL提供了28个素数最为备选方案,__stl_next_prime可以选出一个最接近n且比n要大的素数。
enum { __stl_num_primes = 28 };
static const unsigned long __stl_prime_list[__stl_num_primes] =
{
53ul, 97ul, 193ul, 389ul, 769ul,
1543ul, 3079ul, 6151ul, 12289ul, 24593ul,
49157ul, 98317ul, 196613ul, 393241ul, 786433ul,
1572869ul, 3145739ul, 6291469ul, 12582917ul, 25165843ul,
50331653ul, 100663319ul, 201326611ul, 402653189ul, 805306457ul,
1610612741ul, 3221225473ul, 4294967291ul
};
inline unsigned long __stl_next_prime(unsigned long __n)
{
const unsigned long* __first = __stl_prime_list;
const unsigned long* __last = __stl_prime_list + (int)__stl_num_primes;
const unsigned long* pos = lower_bound(__first, __last, __n);
return pos == __last ? *(__last - 1) : *pos;
}
size_type max_bucket_count() const
{
return __stl_prime_list[(int)__stl_num_primes - 1];
}hash_table的模板参数
template <class _Val, class _Key, class _HashFcn,
class _ExtractKey, class _EqualKey, class _Alloc>其中
// 重新调整表格大小
template <class _Val, class _Key, class _HF, class _Ex, class _Eq, class _All>
void hashtable<_Val,_Key,_HF,_Ex,_Eq,_All>
::resize(size_type __num_elements_hint)
{
const size_type __old_n = _M_buckets.size();
// 超过原来表格的大小时才进行调整
if (__num_elements_hint > __old_n) {
// 新的表格大小
const size_type __n = _M_next_size(__num_elements_hint);
// 在边界情况下可能无法调整(没有更大的素数了)
if (__n > __old_n) {
vector<_Node*, _All> __tmp(__n, (_Node*)(0),
_M_buckets.get_allocator());
__STL_TRY {
// 填充新的表格
for (size_type __bucket = 0; __bucket < __old_n; ++__bucket) {
_Node* __first = _M_buckets[__bucket];
while (__first) {
size_type __new_bucket = _M_bkt_num(__first->_M_val, __n);
_M_buckets[__bucket] = __first->_M_next;
__first->_M_next = __tmp[__new_bucket];
__tmp[__new_bucket] = __first;
__first = _M_buckets[__bucket];
}
}
// 通过swap交换
_M_buckets.swap(__tmp);
}
# ifdef __STL_USE_EXCEPTIONS
// 异常处理
catch(...) {
for (size_type __bucket = 0; __bucket < __tmp.size(); ++__bucket) {
while (__tmp[__bucket]) {
_Node* __next = __tmp[__bucket]->_M_next;
_M_delete_node(__tmp[__bucket]);
__tmp[__bucket] = __next;
}
}
throw;
}
# endif /* __STL_USE_EXCEPTIONS */
}
}
}unordered_map
unordered_map是以hash_table为底层容器来实现的。
算法
STL算法部分主要由头文件,,组成。要使用 STL中的算法函数必须包含头文件,对于数值算法须包含,中则定义了一些模板类,用来声明函数对象。
STL中算法大致分为四类:
1. 非可变序列算法:指不直接修改其所操作的容器内容的算法。
2. 可变序列算法:指可以修改它们所操作的容器内容的算法。
3. 排序算法:包括对序列进行排序和合并的算法、搜索算法以及有序序列上的集合操作。
4. 数值算法:对容器内容进行数值计算。
stl中大概有70个算法,不再一一列举。接下来介绍STL中最庞大的sort()排序算法。
sort:
sort接受两个RandomAccessIterators(随机存取迭代器),然后将区间内的所有元素以渐增方式从小到大排列。第二个版本允许用户指定一个仿函数作为比较的标准。
STL的sort()算法,数据量大时采用Quick Sort,分段递归排序,一旦分段后的数据量小于某个门槛,为避免Quick Sort的递归调用带来过大的额外负荷,就改用Insertion Sort。如果递归层次过深,还会改用Heap Sort。
Insertion Sort是《算法导论》一开始就讨论的算法。它的基本原理是:将初始序列的第一个元素作为一个有序序列,然后将剩下的N-1个元素按关键字大小依次插入序列,并一直保持有序。这个算法的复杂度为O(N^2),最好情况下时间复杂度为O(N)。在数据量很少时,尤其还是在序列“几近排序但尚未完成”时,有着很不错的效果。
Insertion Sort
// 默认以渐增方式排序
template <class RandomAccessIterator>
void __insertion_sort(RandomAccessIterator first,
RandomAccessIterator last)
{
if (first == last) return;
// --- insertion sort 外循环 ---
for (RandomAccessIterator i = first + 1; i != last; ++i)
__linear_insert(first, i, value_type(first));
// 以上,[first,i) 形成一个子区间
}
template <class RandomAccessIterator, class T>
inline void __linear_insert(RandomAccessIterator first,
RandomAccessIterator last, T*)
{
T value = *last; // 记录尾元素
if (value < *first){ // 尾比头还小 (注意,头端必为最小元素)
copy_backward(first, last, last + 1); // 将整个区间向右移一个位置
*first = value; // 令头元素等于原先的尾元素值
}
else // 尾不小于头
__unguarded_linear_insert(last, value);
}
template <class RandomAccessIterator, class T>
void __unguarded_linear_insert(RandomAccessIterator last, T value)
{
RandomAccessIterator next = last;
--next;
// --- insertion sort 内循环 ---
// 注意,一旦不再出现逆转对(inversion),循环就可以结束了
while (value < *next){ // 逆转对(inversion)存在
*last = *next; // 调整
last = next; // 调整迭代器
--next; // 左移一个位置
}
*last = value; // value 的正确落脚处
}上述函数之所以命名为unguarded_x是因为,一般的Insertion Sort在内循环原本需要做两次判断,判断是否相邻两元素是”逆转对“,同时也判断循环的行进是否超过边界。但由于上述所示的源代码会导致最小值必然在内循环子区间的边缘,所以两个判断可合为一个判断,所以称为unguarded_。省下一个判断操作,在大数据量的情况下,影响还是可观的。
Quick Sort是目前已知最快的排序法,平均复杂度为O(NlogN),可是最坏情况下将达O(N^2)。
Quick Sort算法可以叙述如下。假设S代表将被处理的序列:
1. 如果S的元素个数为0或1,结束。
2. 取S中的任何一个元素,当做枢轴(pivot) v。
3. 将S分割为L、R两段,使L内的每一个元素都小于或等于v,R内的每一个元素都大于或等于v。
4. 对L、R递归执行Quick Sort。
Median-of-Three(三点中值)
因为任何元素都可以当做枢轴(pivot),为了避免元素输入时不够随机带来的恶化效应,最理想最稳当的方式就是取整个序列的投、尾、中央三个元素的中值(median)作为枢轴。这种做法称为median-of-three partitioning。
Quick Sort
// 返回 a,b,c之居中者
template
inline const T& __median(const T& a, const T& b, const T& c)
{
if (a < b)
if (b < c) // a < b < c
return b;
else if (a < c) // a < b, b >= c, a < c --> a < b <= c
return c;
else // a < b, b >= c, a >= c --> c <= a < b
return a;
else if (a < c) // c > a >= b
return a;
else if (b < c) // a >= b, a >= c, b < c --> b < c <= a
return c;
else // a >= b, a >= c, b >= c --> c<= b <= a
return b;
} Partitioning(分割)
分割方法有很多,以下叙述既简单又有良好成效的做法。令first向尾移动,last向头移动。当*first大于或等于pivot时停下来,当*last小于或等于pivot时也停下来,然后检验两个迭代器是否交错。未交错则元素互相,然后各自调整一个位置,再继续相同行为。若交错,则以此时first为轴将序列分为左右两半,左边值都小于或等于pivot,右边都大于等于pivot
Partitioning
template
RandomAccessIterator __unguarded_partition(
RandomAccessIterator first,
RandomAccessIterator last,
T pivot)
{
while(true){
while (*first < pivot) ++first; // first 找到 >= pivot的元素就停
--last;
while (pivot < *last) --last; // last 找到 <=pivot
if (!(first < last)) return first; // 交错,结束循环
// else
iter_swap(first,last); // 大小值交换
++first; // 调整
}
} Heap Sort:partial_sort(),即heap不断将头取出.
Heap Sort
// paitial_sort的任务是找出middle - first个最小元素。
template <class RandomAccessIterator>
inline void partial_sort(RandomAccessIterator first,
RandomAccessIterator middle,
RandomAccessIterator last)
{
__partial_sort(first, middle, last, value_type(first));
}
template <class RandomAccessIterator,class T>
inline void __partial_sort(RandomAccessIterator first,
RandomAccessIterator middle,
RandomAccessIterator last, T*)
{
make_heap(first, middle); // 默认是max-heap,即root是最大的
for (RandomAccessIterator i = middle; i < last; ++i)
if (*i < *first)
__pop_heap(first, middle, i, T(*i), distance_type(first));
sort_heap(first,middle);
}IntroSort
不当的枢轴选择,导致不当的分割,导致Quick Sort恶化为O(N^2)。David R. Musser于1996年提出一种混合式排序算法,Introspective Sorting。其行为在大部分情况下几乎与 median-of-3 Quick Sort完全相同。但是当分割行为(partitioning)有恶化为二次行为倾向时,能自我侦测,转而改用Heap Sort,使效率维持在O(NlogN),又比一开始就使用Heap Sort来得好。大部分STL的sort内部其实就是用的IntroSort。
template <class RandomAccessIterator>
inline void sort(RandomAccessIterator first,
RandomAccessIterator last)
{
if (first != last){
__introsort_loop(first, last, value_type(first), __lg(last-first)*2);
__final_insertion_sort(first,last);
}
}
// __lg()用来控制分割恶化的情况
// 找出2^k <= n 的最大值,例:n=7得k=2; n=20得k=4
template<class Size>
inline Size __lg(Size n)
{
Size k;
for (k = 0; n > 1; n >>= 1)
++k;
return k;
} // 当元素个数为40时,__introsort_loop的最后一个参数
// 即__lg(last-first)*2是5*2,意思是最多允许分割10层。
const int __stl_threshold = 16;
template <class RandomAccessIterator, class T, class Size>
void __introsort_loop(RandomAccessIterator first,
RandomAccessIterator last, T*,
Size depth_limit)
{
while (last - first > __stl_threshold){ // > 16
if (depth_limit == 0){ // 至此,分割恶化
partial_sort(first, last, last); // 改用 heapsort
return;
}
--depth_limit;
// 以下是 median-of-3 partition,选择一个够好的枢轴并决定分割点
// 分割点将落在迭代器cut身上
RandomAccessIterator cut = __unguarded_partition
(first, last, T(__median(*first,
*(first + (last - first)/2),
*(last - 1))));
// 对右半段递归进行sort
__introsort_loop(cut,last,value_type(first), depth_limit);
last = cut;
// 现在回到while循环中,准备对左半段递归进行sort
// 这种写法可读性较差,效率也并没有比较好
}
}函数一开始就判断序列大小,通过个数检验之后,再检测分割层次,若分割层次超过指定值,就改用partial_sort(),即Heap sort。都通过了这些校验之后,便进入与Quick Sort完全相同的程序。
当__introsort_loop()结束,[first,last)内有多个“元素个数少于或等于”16的子序列,每个序列有相当程序的排序,但尚未完全排序(因为元素个数一旦小于 __stl_threshold,就被中止了)。回到母函数,再进入__final_insertion_sort():
template <class RandomAccessIterator>
void __final_insertion_sort(RandomAccessIterator first,
RandomAccessIterator last)
{
if (last - first > __stl_threshold){
// > 16
// 一、[first,first+16)进行插入排序
// 二、调用__unguarded_insertion_sort,实质是直接进入插入排序内循环,
// *参见Insertion sort 源码
__insertion_sort(first,first + __stl_threshold);
__unguarded_insertion_sort(first + __stl_threshold, last);
}
else
__insertion_sort(first, last);
}
template <class RandomAccessIterator>
inline void __unguarded_insertion_sort(RandomAccessIterator first,
RandomAccessIterator last)
{
__unguarded_insertion_sort_aux(first, last, value_type(first));
}
template <class RandomAccessIterator, class T>
void __unguarded_insertion_sort_aux(RandomAccessIterator first,
RandomAccessIterator last,
T*)
{
for (RandomAccessIterator i = first; i != last; ++i)
__unguarded_linear_insert(i, T(*i));
}

