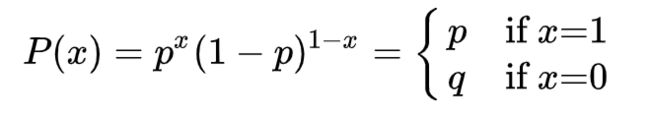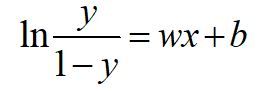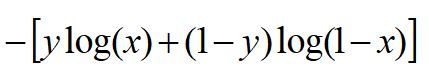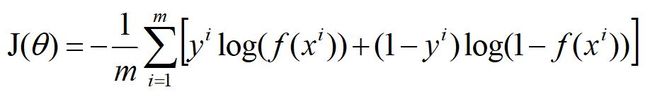逻辑回归从入门到深入（logistic regression)

怎么讲述逻辑回归？

（面试官：请你简单介绍一下逻辑回归）

从以下几个方面入手

• 逻辑回归是什么

• 逻辑回归的损失函数，有什么优势

• 逻辑回归怎么迭代的

• 逻辑回归有什么优缺点

逻辑回归是什么

逻辑回归一种线性回归模型，它假设数据服从伯努利分布，通过极大似然函数的方法，运用梯度下降法来求解参数，进而大道二分类的目的。

伯努利分布(Bernoulli distribution)，也称为两点分布或者0-1分布，是最简单的离散型概率分布。我们记成功概率为p(0≤p≤1)，则失败概率为q=1-p，则：

正类为1，负类为0，显然是服从0-1分布

伯努利分布

更多详细内容看下面的大牛博客。

大牛博客https://www.cnblogs.com/ModifyRong/p/7739955.html

大部分内容都来自于这位大牛

逻辑回归的损失函数，为什么用它？

交叉熵损失，通过极大似然估计算出来的就是交叉熵损失，之前的博客只是对交叉熵损失有个感性的认识，并没有推导。

有什么优势？

1 一般和平方损失比较，平方损失加上sigmoid函数将会是一个非凸的函数，非凸函数会得到局部最优解，

用对数似然函数得到的高阶连续可导凸函数，是全局最优解。

2 参数的迭代并不设计到sigmoid函数，从而避免了sigmoid的梯度消失问题。

要是选择其他损失函数，例如MSE，参数迭代的公式里就会有sigmoid函数本身，而sigmoid函数有梯度消失问题，这样训练会很慢

逻辑回归优缺点

优点：

形式简单，可解释强

训练速度比较快

缺点：

准确率可能不高

处理非线性数据比较麻烦，需要做大量的特征工程

--------------------------------------------------------------------------------------------------

1 引言

    最近做一个项目，准备用逻辑回归来把数据压缩到[-1,1]，但最后的预测却是和标签类似（或者一样）的预测。也就是说它的predict的结果不是连续的，而是类别，1,2,3,...k。对于predict_proba，这是预测的概率，但概率有很多个，数目为训练集类别（label）的个数。逻辑回归的原理，就是取出最大概率对应的类别。

    所以逻辑回归，不是回归，而是分类器，二分类，多分类。

    逻辑回归，是一个很有误导性的概念。

    这是个人最近的体会，入门的读者请忽略。

2 线性回归

    先说一下，一般模型的训练和预测过程：

    1，训练：通过训练数据来训练模型，也就是通常我们所说的学习过程，即确定模型的参数。

    2， 预测：训练过后，模型参数确定，有预测数据输入，就会得到一个结果。

    常见的线性回归y=wx+b,我们通过训练集来训练出我们的模型，也就是得到我们的模型参数w,b，这样，我们的直线或者超平面(x是多维的)就确定了。接着，对于测试集，来了一个数据x，w,b已经学习出来了，带入y=wx+b，就会得到一个y值，也就是我们的预测值。注意， 它是浮点数。

    这里得到的y为什么叫回归呢，因为y不是类别（label）中的一个，它是预测出来的实数（大部分是小数）。

    有的同学可能不理解什么是回归？我解释一下：

     首先，需要明白二分类，类别/标签/label是二值，{0，1}或{-1，1}，总之它的类别数两个。相信你已经知道多分类了，就是类别是多值的，{0，1，2，3，4}等，这是5类。那么回归是什么你呢。回归的取值，就不是像分类这样取整数了，它是小数，浮点数，是连续的，例如（0，1）之间的取值等。

3 逻辑回归

    前面已经说了，虽然它不是回归，但是名字已经确定了，大家还是这么叫的。

    前面的线性回归，我们已经得到y=wx+b。它是实数，y的取值范围可以是（负无穷，正无穷）。现在，我们不想让它的值这么大，所以我们就想把这个值给压缩一下，压缩到[0,1]。什么函数可以干这个事呢？研究人员发现signomid函数就有这个功能。所以，他们就尝试着，用signomid函数搞一搞这个y。

sigmoid的函数如下：

                        

sigmoid的图像如下：

    

压缩，就是把y=wx+b带入sigmoid(x)。把这个函数的输出，还定义为y,即：

        

这样，y就是（0，1）的取值。

把这个式子变换一下：

        

4 损失函数

损失函数，通俗讲，就是衡量真实值和预测值之间差距的函数。所以，我们希望这个函数越小越好。在这里，最小损失是0。

以二分类（0，1）为例：

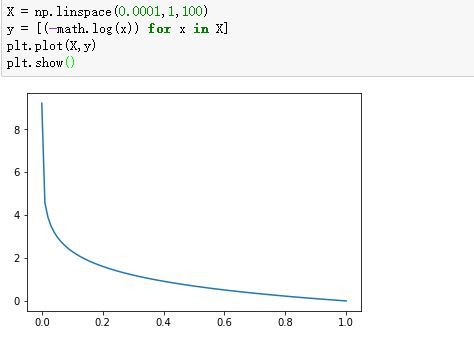
当真值为1，模型的预测输出为1时，损失最好为0，预测为0是，损失尽量大。

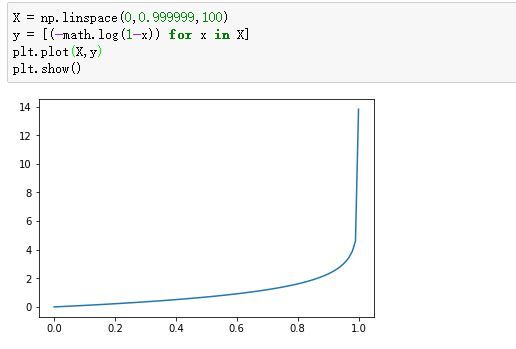
同样的，当真值为0，模型的预测输出为0时，损失最好为0，预测为1是，损失尽量大。

所以，我们尽量使损失函数尽量小，越小说明预测的越准确。

这个损失函数为：

    

我们看看这个函数的图像：

-log(x):

-log(1-x):

所以，我们压缩之后，预测y在0-1之间。我们利用这个损失函数，尽量使这个损失小，就能达到很好的效果。

我们把这两个损失综合起来：

y就是标签，分别取0，1，看看是不是我们前面写的那两个损失函数。

对于m个样本，总的损失：

这个式子中，m是样本数，y是标签，取值0或1，i表示第i个样本，f(x)表示预测的输出。

不过，当损失过于小时，也就是模型能拟合全部/绝大部分的数据，就有可能出现过拟合。这种损失最小是经验风险最小，为了不让模型过拟合，我们又引入了其他的东西，来尽量减小过拟合，就是大家所说的结构风险损失。

结构经验风险常用的是正则化，L0，L1，L2正则化

5 sklearn中的应用

penalty=l2, # 惩罚项，可选l1,l2，对参数约束，减少过拟合风险
dual=False, # 对偶方法（原始问题和对偶问题），用于求解线性多核（liblinear)的L2的惩罚项上。样本数大于特征数时设置False
tol=0.0001, # 迭代停止的条件，小于等于这个值停止迭代，损失迭代到的最小值。
C=1.0, # 正则化系数λ的倒数，越小表示越强的正则化。这个正则化系数并没有加到正则化项前面，而是经验损失前面，C越大，正则化项权重（始终未1）相对就小，倒数，我认为是相对的。【自认为，求指正】
fit_intercept=True, # 是否存在截距值，即b
intercept_scaling=1, #
class_weight=None, # 类别的权重，样本类别不平衡时使用，设置balanced会自动调整权重。为了平横样本类别比例，类别样本多的，权重低，类别样本少的，权重高。
random_state=None, # 随机种子
solver=’liblinear’, # 优化算法的参数，包括newton-cg,lbfgs,liblinear,sag,saga,对损失的优化的方法
max_iter=100,# 最大迭代次数，
multi_class=’ovr’,# 多分类方式，有‘ovr','mvm'
verbose=0, # 输出日志，设置为1，会输出训练过程的一些结果
warm_start=False, # 热启动参数，如果设置为True,则下一次训练是以追加树的形式进行（重新使用上一次的调用作为初始化）
n_jobs=1 # 并行数，设置为1，用1个cpu运行，设置-1，用你电脑的所有cpu运行程序
                                            )

有重要的一点 

class_weight: balanced 这个怎么计算的

官网上nsamples/(nclasses*np.bincount(y))

某一类样本的权重 ：  总样本数/(类别数*某一类对应的样本个数)

假如样本标签【1，0，1，0，0，1，1，0，1，1】，共10个样本，6个为正，4个为负

正样本的权重： 10/(2*6) = 5/6， 负样本的权重：10/(2*4)=5/4

这就是前面说的：类别样本多的，权重低，类别样本少的，权重高.

np.bincount() 什么意思呢？从名字来看，分桶计数，这里分桶的步长默认为1，然后统计每一桶的样本个数。

还是这个例子【1，0，1，0，0，1，1，0，1，1】，分桶长度=最大数+1，这个要分2桶，结果[4, 6]

所以对应公式 10/(2*[4,6]) = [5/4, 5/6], 这里用分数表示，实际返回的是小数。

 

5.1 solver 各参数详解

    损失函数的选择，主要有liblinear(线性分类器库)，sag,saga,newton-cg,lbfgs

 

•     对于小的数据集，选择‘liblinear’较好；对于大的数据集，选择'sag'或者‘saga’，它们的速度更快
• 对于对分类问题，只能用sag,saga,newton-cg,lbfgs；对于多项式损失，'liblinear'只限于1对多的问题。

• sag，newton-cg，lbfgs，只能用于L2正则化，liblinear，saga还可以用于L1正则化

5.1.1 liblinear

 liblinear: A Library for Large Linear Classification

 liblinear是国立台湾大学林智仁（Chih-Jen Lin）老师团队开发的，他们还开发了libsvm。

 liblinear是一个线性分类器，它支持：

L2-regularizedL1-loss Support VectorClassification # L2正则化项，L1损失函数的SVM分类器

L2-regularizedL2-loss Support Vector Classification  # L2正则化项，L2损失函数的SVM分类器

L1-regularizedL2-loss Support Vector Classification  # L1正则化项，L1损失函数的SVM分类器

L2-regularized Logistic Regression  # L2正则逻辑回归

L1-regularized Logistic Regression # L1正则逻辑回归

sklearn参数中的penalty=L2,就是采用上面的L2正则逻辑回归，是对参数矩阵W做了平方。

 

5.1.2 sag

sag ：Stochastic Average Gradient（随机平均梯度）

 

6 逻辑回归需要归一化吗

先说结论，逻辑回归不需要归一化。

即使是量纲不一样，因为变量x前面有权重w，通过训练，w会对x进行调整。

像基于距离计算的算法KNN，SVM就需要归一化。

像欧式距离，a，b前面没有系数，如果a=10, b=0.1，b的值太小，它的价值会被湮没。

能够谈到逻辑回归需不需要归一化的场景，个人认为是逻辑回归做回归任务时。

在做分类时，一般要对数据进行处理，类别型one-hot，连续值会进行分桶，分桶之后进行one-hot, 整体数据只有0,1。

参考 

https://stats.stackexchange.com/questions/48360/is-standardization-needed-before-fitting-logistic-regression

https://www.datacamp.com/community/tutorials/preprocessing-in-data-science-part-2-centering-scaling-and-logistic-regression