实验目的
梯度下降法是一个最优化算法,通常也称为最速下降法。最速下降法是求解无约束优化问题最简单和最古老的方法之一,虽然现已不具有实用性,但是许多有效算法都是以它为基础进行改进和修正而得到的。最速下降法是用负梯度方向为搜索方向的,最速下降法越接近目标值,步长越小,前进越慢。
线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。其表达形式为y = w'*x+e,e为误差服从均值为0的正态分布。[1]
回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
本次实验将验证梯度下降法可以求解线性回归的参数。
实验环境
本次实验,使用的程序语言为Python3.5,依赖的工具包为:
import matplotlib.pyplot as plt
import csv
import numpy as np
import pandas as pd
from mpl_toolkits.mplot3d import Axes3D
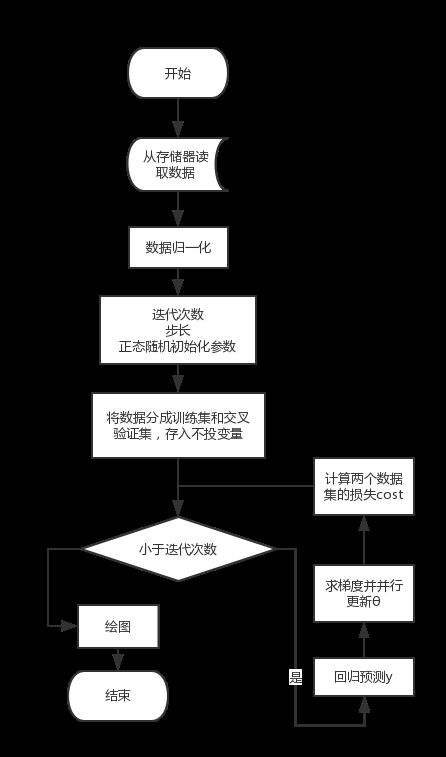
实验内容及步骤
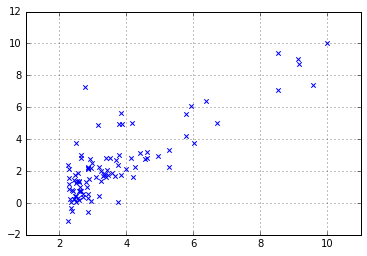
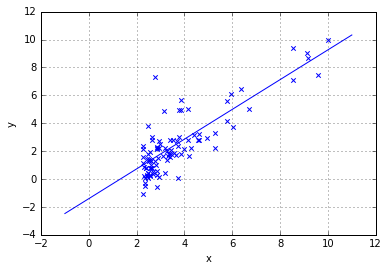
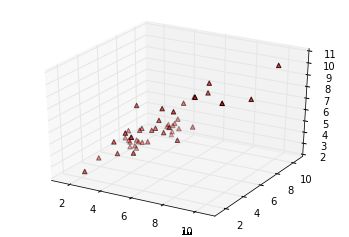
ü 画出样本分布图;
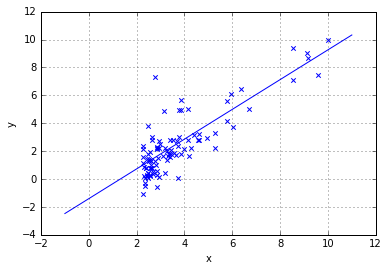
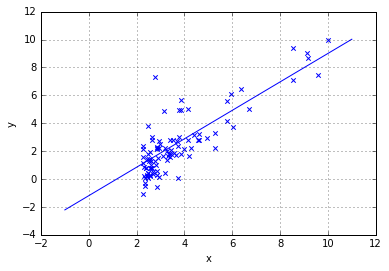
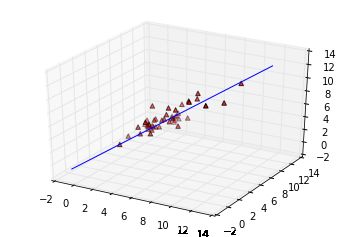
ü 画出线性回归假设模型;
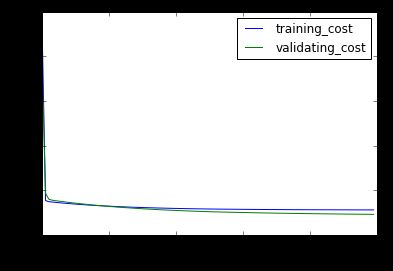
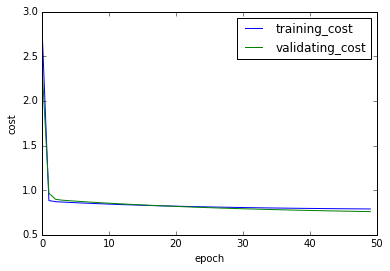
ü 画出成本函数收敛曲线
ü 使用梯度下降法更新参数
在详细了解梯度下降的算法之前,我们先看看相关的一些概念。
步长(Learning rate):步长决定了在梯度下降迭代的过程中,每一步沿梯度负方向前进的长度。用上面下山的例子,步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度。
特征(feature):指的是样本中输入部分,比如样本(x0,y0),(x1,y1),则样本特征为x,样本输出为y。
假设函数(hypothesis function):在监督学习中,为了拟合输入样本,而使用的假设函数,记为hθ(x)。
损失函数(loss function):为了评估模型拟合的好坏,通常用损失函数来度量拟合的程度。损失函数极小化,意味着拟合程度最好,对应的模型参数即为最优参数。在线性回归中,损失函数通常为样本输出和假设函数的差取平方。
预测值:
h_θ (x)=x^T θ
误差:
J(θ)=1/2m ∑i=1~m〖[(h]θ (x(i) )-y(i) 〗 )^2
优化目标:
min┬θ〖Jθ 〗
参数更新:
θ=θ-α 1/m 〖((h-y)x)〗^T
实验结果及分析
对数据进行了归一化处理。
对1维数据,迭代了300次0.02步长,500次0.01步长。最终结果如图:
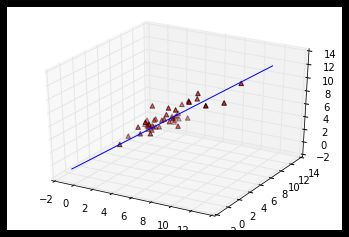
对2维数据,迭代了700次0.01步长。最终结果如图:
如何调优?步长,初始参数,归一化。
方法变种:批量梯度下降,随机梯度下降,小批量。在每次选取样本的数量上有区别。
横向比较:梯度下降法和最小二乘法相比,梯度下降法需要选择步长,而最小二乘法不需要。梯度下降法是迭代求解,最小二乘法是计算解析解。如果样本量不算很大,且存在解析解,最小二乘法比起梯度下降法要有优势,计算速度很快。但是如果样本量很大,用最小二乘法由于需要求一个超级大的逆矩阵,这时就很难或者很慢才能求解解析解了,使用迭代的梯度下降法比较有优势。梯度下降法和牛顿法/拟牛顿法相比,两者都是迭代求解,不过梯度下降法是梯度求解,而牛顿法/拟牛顿法是用二阶的海森矩阵的逆矩阵或伪逆矩阵求解。相对而言,使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。
程序
1.ipynb
%matplotlib inline
import matplotlib.pyplot as plt
import csv
import numpy as np
import pandas as pd
因为一开始收敛效果不好,然后做了数据整理,方案是全部映射到10以内一个数量级,归一化。
data=pd.read_csv('./1D.csv',header=None)
data=np.array(data)
div=np.array([max(data[:,0]),max(data[:,1])])
data=data/div*10
print(data.shape)
(97, 2)
num=10
val_x=np.ones((num,data.shape[1]))
sam_x=np.ones((data.shape[0]-num,data.shape[1]))
sam_x[:,1:]=data[:-num,:-1]
sam_y=data[:-num,-1:]
print("sx.shape",sam_x.shape,"sy.shape",sam_y.shape)
val_x[:,1:]=data[-num:,:-1]
val_y=data[-num:,-1:]
print("vx.shape",val_x.shape,"vy.shape",val_y.shape)
sx.shape (87, 2) sy.shape (87, 1)
vx.shape (10, 2) vy.shape (10, 1)
plt.scatter(data[:,0],data[:,-1],marker='x')
plt.grid()
# 预测值
def predict(theta,x):
'''
theta:(2,1)
x:(n,2)
'''
return x.dot(theta).reshape((-1,1))
np.random.seed(1502520028)
# print(data.shape)
theta=np.random.normal(size=(2,1))
print(theta)
epoch=300
alpha=0.02
eps=0.1
# 定义成常量计算快
def const_error(h,y):
return h-y
# 均方误差
# h:pred_y
def cost(h,y,con):
return (np.mean(con**2))/2
def grad(x,con):
return np.mean(con*x,axis=0,keepdims=True).transpose()
[[-0.40838329]
[ 1.31489742]]
sc=[]#训练集误差
vc=[]#交叉集预测误差
for i in range(epoch):
h=predict(theta,sam_x)
con=const_error(h,sam_y)
g=grad(sam_x,con)
theta=theta-alpha*g
if i%(epoch//50)==0:
sc.append(cost(h,sam_y,con))
pre_y=predict(theta,val_x)
vc.append(cost(pre_y,val_y,const_error(pre_y,val_y)))
plt.plot(np.arange(len(sc)),np.array(sc),label="training_cost")
plt.legend()
plt.plot(np.arange(len(vc)),np.array(vc),label="validating_cost")
plt.legend()
plt.xlabel("epoch")
plt.ylabel("cost")
plt.scatter(data[:,0],data[:,-1],marker='x')
plt.grid()
temp_x=np.linspace(-1,11,100)
plt.plot(temp_x,(theta[1]*temp_x+theta[0]))
plt.xlabel("x");plt.ylabel("y")
print("y=%-.2f%+.2f*x1" % (theta[0],theta[1]))
y=-1.20+1.02*x1
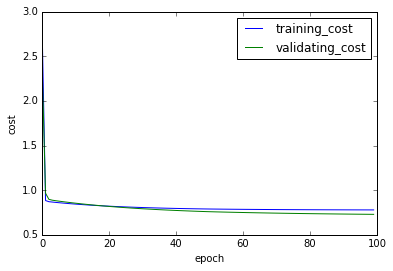
在上一阶段,两个损失的收敛速度已经变慢,那么我们又增加500次训练。
为了避免在极值点处震荡,同时减小步长到0.01
epoch=500
alpha=0.01
print("我真的还想再活500年")
for i in range(epoch):
h=predict(theta,sam_x)
con=const_error(h,sam_y)
g=grad(sam_x,con)
theta=theta-alpha*g
if i%(epoch//50)==0:
sc.append(cost(h,sam_y,con))
pre_y=predict(theta,val_x)
vc.append(cost(pre_y,val_y,const_error(pre_y,val_y)))
plt.plot(np.arange(len(sc)),np.array(sc),label="training_cost")
plt.legend()
plt.plot(np.arange(len(vc)),np.array(vc),label="validating_cost")
plt.legend()
plt.xlabel("epoch")
plt.ylabel("cost")
我真的还想再活500年
plt.scatter(data[:,0],data[:,-1],marker='x')
plt.grid()
temp_x=np.linspace(-1,11,100)
plt.plot(temp_x,(theta[1]*temp_x+theta[0]))
plt.xlabel("x");plt.ylabel("y")
print("y=%-.2f%+.2f*x1" % (theta[0],theta[1]))
y=-1.41+1.07*x1
2.ipynb
%matplotlib inline
import matplotlib.pyplot as plt
import csv
import numpy as np
import pandas as pd
from mpl_toolkits.mplot3d import Axes3D
数据整理方案是全部映射到10以内一个数量级,归一化。
data=pd.read_csv('./2D.csv',header=None)
data=np.array(data)
div=np.array([max(data[:,0]),max(data[:,1]),max(data[:,2])])
data=data/div*10
print(data.shape)
(47, 3)
num=8
val_x=np.ones((num,data.shape[1]))
sam_x=np.ones((data.shape[0]-num,data.shape[1]))
sam_x[:,1:]=data[:-num,:-1]
sam_y=data[:-num,-1:]
print("sx.shape",sam_x.shape,"sy.shape",sam_y.shape)
val_x[:,1:]=data[-num:,:-1]
val_y=data[-num:,-1:]
print("vx.shape",val_x.shape,"vy.shape",val_y.shape)
sx.shape (39, 3) sy.shape (39, 1)
vx.shape (8, 3) vy.shape (8, 1)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(data[:,0],data[:,1],data[:,-1],c='r',marker='^',depthshade=True)
# 预测值
def predict(theta,x):
'''
theta:(3,1)
x:(n,3)
'''
return x.dot(theta).reshape((-1,1))
np.random.seed(1502520028)
# print(data.shape)
theta=np.random.normal(size=(3,1))
print(theta)
epoch=700
alpha=0.01
eps=0.1
# 定义成常量计算快
def const_error(h,y):
return h-y
# 均方误差
# h:pred_y
def cost(h,y,con):
return (np.mean(con**2))/2
def grad(x,con):
return np.mean(con*x,axis=0,keepdims=True).transpose()
[[-0.40838329]
[ 1.31489742]
[-1.82310129]]
sc=[]#训练集误差
vc=[]#交叉集预测误差
for i in range(epoch):
h=predict(theta,sam_x)
con=const_error(h,sam_y)
g=grad(sam_x,con)
theta=theta-alpha*g
if i%(epoch//100)==0:
sc.append(cost(h,sam_y,con))
pre_y=predict(theta,val_x)
vc.append(cost(pre_y,val_y,const_error(pre_y,val_y)))
plt.plot(np.arange(len(sc)),np.array(sc),label="training_cost")
plt.legend()
plt.plot(np.arange(len(vc)),np.array(vc),label="validating_cost")
plt.legend()
plt.xlabel("epoch")
plt.ylabel("cost")
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.scatter(data[:,0],data[:,1],data[:,-1],c='r',marker='^',depthshade=True)
temp_x=np.linspace(-1,12,100)
ax.plot(temp_x,temp_x,(theta[2]*temp_x+theta[1]*temp_x+theta[0]))
print("y=%-.2f%+.2f*x1%+.2f*x2" % (theta[0],theta[1],theta[2]))
y=0.17+0.90*x1+0.11*x2