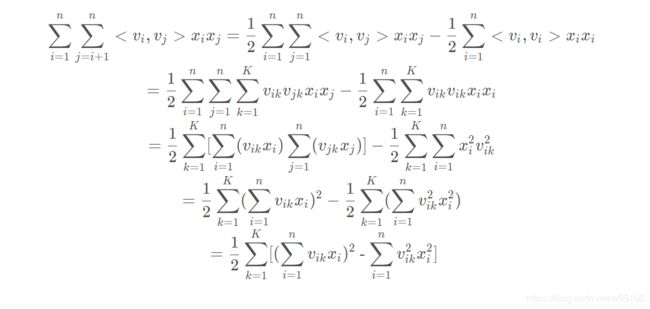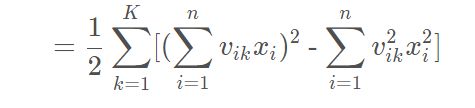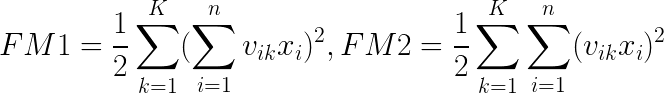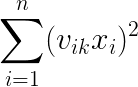deepFM in pytorch

前言

学这些东西的过程，就是感受知识以反人类的方式传播的过程。

五花八门的表演、措辞、逻辑，每个作者书写时都有自己的dialect，就像听老外不同的accent一样。

科技树往上爬，没人出来做阶梯状的体系整理，导致不同的作者默认你的预备知识结构不同，又不给例子也不讲解中途变化的......

看一样东西费好久也未必能找到一篇能说清楚的文章。

不得不感慨，能做到深入浅出的优秀连接器还是太少了。

就是这种十年一出的连接器太少，才让广义学术与普通人的生活间隔太远。

无怪听说过丘成桐的少于陈景润的，知道高锟的少于杨振宁的。

 

 

理论部分

 

①DeepFM

因为作者是中国人，所以起名方式就比较耿直了，基本是九年义务教育看得懂的水平。

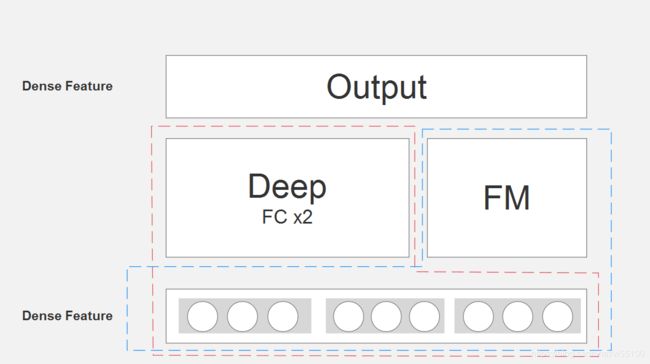
这东西的结构画出来，就是左边deep network，右边FM，所以叫deepFM。

(网上的图已经传播到像素模糊了...只能手动重绘)

其中deep部分并不怎么deep，才2个全连接层（FC），入门DL的人应该都看得懂。

 

②FM(Factorization machines)，因子分解机部分

在传统的一阶线性回归之上，加了一个二次项。

上面这条式子严格来说只能叫【FM的二阶公式】，理论可以推广到n阶。

 

资料:

请务必看这篇大佬在2014年的研习文章，写的太好了 皮果提《Factorization Machines 学习笔记（二）模型方程》

还有这位用Katex手打公式的老哥 ·清尘·《FM、FMM、DeepFM整理（pytorch）》

对理论有了一知半解之后再往下结合我的代码理解。

 

#原论文
@inproceedings{guo2017deepfm,
  title={DeepFM: A Factorization-Machine based Neural Network for CTR Prediction},
  author={Huifeng Guo, Ruiming Tang, Yunming Ye, Zhenguo Li and Xiuqiang He},
  booktitle={the Twenty-Sixth International Joint Conference on Artificial Intelligence (IJCAI)},
  pages={1725--1731},
  year={2017}
}
#https://www.ijcai.org/proceedings/2017/0239.pdf


#因子分解机论文
https://www.csie.ntu.edu.tw/~b97053/paper/Rendle2010FM.pdf

 

当前环境的主流似乎还是tensorflow。

但我实在不喜欢tensorflow这种图结构，所以学习的是pytorch版本。

 

代码部分

 

1.对单个feature的稀疏向量进行紧凑化处理

首先是sparse vector到 dense vector的embedding层。

前置知识是离散特征的向量化，需要自学。

例如，调包侠常用的sklearn包里的onehotencoder,countvectorizer之类的。

这里假设你已经会了。

#讲人话时间

#假设有特征gender
values = (man,female,trans)
#one-hot之后会得到长为3的vector
#e.g. 
v = [0,1,0]

#如果取值有10万种，那么len(v)=10^5，而这么长的vector里面只有一个1
#我们希望把它压缩到一个比较亲近人类的长度，e.g.300
#于是有
feature_size = 10^5
embedding_size= 300

#构建embedding层
import torch
import torch.nn as nn

embd_layer = nn.Embedding(feature_size, embedding_size) 

#很简单吧

 

2.从单feature扩展到n个feature

#现在我们有n个feature
#每个feature的取值分别有feature_size种，存在一个list中。

#伪代码
features = [age,gender,work]
feature_sizes = []
for feature in features:
    feature_szie=len(feature)
    feature_sizes.append(feature_size)
    

#于是我们可以求相关参数

#在FM算法中，作者把一个字段作为一个field，于是我们可以根据传入的参数，知道有多少个field
n_fields = len(feature_sizes)


#再对每一个field都建立embedding
embedding_size = 300
embd_layers = nn.ModuleList(
    [nn.Embedding(feature_size, embedding_size) for feature_size in self.feature_sizes]
)

#我们希望每一种feature，embd之后的size都是相同的，所以这里统一使用了300。
#complete! 也很简单吧！

 

完成之后我们得到了更加紧凑的dense feature，注意这个dense_feature是embd层的输出的水平拼接。

把n个300维的向量拼接的做法就不用说了吧。

所以可以算得其 dim = n个field * 每个300维  = 300*n 维 

 

 

3.Deep部分，把dense_feature丢进神经网络

 

#把300*n维的维度信息提出来
dense_dim =  n_fields * embedding_size

#设定两个全连接层的维度，简便起见假设它们维度相同
fc_dim = 100


#现在我们要丢dense_feature进去

self.fc_layer1 = nn.Sequential(
            nn.Linear(dense_dim,fc_dim),
            nn.BatchNorm2d(fc_dim),
            nn.LeakyReLU(0.2, inplace=True)     
)

self.fc_layer2 = nn.Sequential(
            nn.Linear(fc_dim,fc_dim),
            nn.BatchNorm2d(fc_dim), 
            nn.LeakyReLU(0.2, inplace=True)     
)


#经过2层之后，
#过于简单，引起舒适

 

我们进行的是如图的这部分：

 

 

4.FM部分，根据sparse feature计算二阶项的预测值

 

这一部分的重点在于参数共享，也是deepFM的创新点之一。

 

(公式来源网络)

 

#参看上图公式
#在deepFM论文中，作者让FM部分的参数k，等同于deep部分embd后的向量长度
#这样就达成了共享参数的目的

#所以我们知道
k = embedding_size = 300

#所以对feature

 

对每一个field，都有一个(feature_size,embedding_size)的参数矩阵。

还是以gender为例，这个矩阵shape=(3,300)

直接上结果。

默认你已经自学完成了理论部分。

那么这就是参数共享了，因为形状一样，所以可以用embd层的参数矩阵，去代替FM部分隐因子的参数矩阵。（理直气壮）

The embedding layer for sparse features in the DNN shares the parameters with the latent vectors (factors) of the FM layer.

 

现在，我们的问题就是，如何用代码来表达推导公式：

备注：原论文的版本，把小k换成小f，网上流传的也多是遵循原版使用字符f。字母不影响达意。

我们把这个式子分为两部分。

则，原式 = FM1-FM2

考虑下列过程

 容易知道，v'x的每一行都是 k=f 时的，

例如v'x的第1行是k=1时的上式。而v'x的shape = (k,1)，是一个k维的列向量，共含有k个元素。

显然我们只需要对v'x的k个元素，逐个平方，再sum，接着乘1/2，即可得到FM1。

 

再考虑下述过程。

如果你用过matlab之类的东西，应该知道点运算。 【.^2】表示逐元素取平方。

 显然(v.^2)'·(x.^2) 的每一行的，都是k=f时的

我们只需要对(v.^2)'·(x.^2) 的每行sum加和，接着乘1/2，即可得到FM2。

 

这就是FM因子分解机理论上的计算方式了。

然而这样做的操作量很大，每个矩阵大小=n*k = feature_size * embedding_size 。

 

又考虑到，我们输入的特征向量x是稀疏的！

虽然shape=(n,1)，但是n个元素里面只有1个1，其他(n-1)个都是0！

 

那么，假设我们知道那个1的下标值，例如我们知道xi=1，而其他的 xj = 0 , ( j=1,2,3,...n, j ≠ i )。

我们的整个计算过程，就可以只关注vi ,shape = (1,k)，和 xi , shape = (1,1)

而xi=1，怎么乘都不影响vi的值，所以进一步的，我们只需要关注vi。

这样计算值就极大地缩减了。

（当然，为了让模型具备泛化能力，我们先不假定xi=1，而是假定xi等于某个不为0的数字。）

于是，最终我们需要的结果就转变成了，vi·xi ，xi是一个很可能为1的数字，vi是(1,k)行向量。

 

这就是为什么在ad_ctr等领域你才能看到FM理论的大量应用，因为这些地方的特征都是极为稀疏的。

【特征的特征决定了我们选取的处理特征的理论】

 

而上文说过，由于我们强行令参数共享，所以 v=embedding矩阵，shape=(feature_size,embedding_size)。

#先构筑一个简单的embd层，
embedding_size=1
feature_size=3
embd_layer = torch.nn.Embedding(feature_size,1)

#如果对第n个field，我们知道一个下标i，使得xi为当前field的唯一非0值。
idx = 1
#在pytorch中，我们可以这样取出vi 
vi = embd_layer(idx) #shape = (1,embedding_size) =(1,k)


#----------------
#如果对第n个field，我们有m个样本的下标构成一个tensor
batch_idx = torch.Tensor([0,1,2])    #shape=(m)
batch_vis = embd_layer(batch_idx)    #shape=(m,k)

#再有m个样本的对应xi的值
batch_xis = torch.FloatTensor([1,1,1]) #shape=(m)

#我们让每个样本的vi与对应的xi相乘
res = (batch_vis.t())*batch_xis       #(k,m)*(m)=(k,m)
res = res.t()                         #shape=(m,k)

#由前面的讨论知道，此时res的每行，
#都是第m个样本在第n个field的(v'x)'=vixi，即长度为k的行向量
#[vi1xi,vi2xi,...,vikxi]

我们解决了一个field内m个sample的问题，现在可以把问题扩展到全部n个field了。

 

回顾公式

 

Remarks:

我学在这里的时候对n的含义犯蒙了很久。

FM算法说，n是input向量x的维数，n=len(x)。

可是网上流传的implementation中，又引入了n=n_field概念。可我们明知道每个field的长度>=1，这样一来len(x)>=n_filed。

现给予解答如下。

以下描述为个人推定的猜想事实，可能有误。

①原始的FM算法(2010)里，作者并未提到field概念。x是单纯的一个任意输入的n维向量，我们对其中的每一个维度xi，构造一个辅助向量vi,shape=(1,k)。

你可以有2个特征，一个比如说是'price'，就是个1维的数字，另一个比如说'status'，是ont-hot处理之后的10维向量。

这两个特征拼接到一起形成一个输入，n=11就是它们拼接后的总长度。

这是n的原始概念，FM的作者并未限制n的特化。

②传播发展的过程中，出现了Field-awarness FM即FFM算法，区别在于embedding的时候引入了Field概念。效果优于单纯的FM。

就好像三百年前，人们说'车'这个词指马车，后来有了汽车，现在人们提到‘车’第一反应就是汽车。

概念由于知识的进步被上位替代了。

或者说，由于现在入门的学生，可以一次性回顾、学习间隔十年之久的所有模型，对不同模型的概念产生了混用。

于是这批中继学习人员写的文章，就混用了一批相似度很高、具备继承关系的模型的概念。

于是现在的人们，哪怕去使用FM，也会带上field的概念。

③ 对上一条的佐证是，我在2014、2013年讲述FM的文章里，就看不到field这种说法。

可见知识入侵、概念交叉是近年来逐渐发生的。

④有趣的是，可以证明，哪怕混用了field概念，也不会影响FM算法的有效性。

因为原算法足够【平凡】。

用一图来证明。

容易知道，在带field概念的FM算法中，n=n_field。

如果假设，平均每个field长 avg_len = 4，那么有 len(input) = 4*n，显然大于n。

 

但是有趣之处在哪呢，因为我们的input是稀疏的，每个field内只有有限个（通常为1个）取值非0。

于是，我们可以将n个field内，p个非0值提出来，拼接成长为p的一维向量，作为当前sample的input* 。

这样就从【带field概念的FM算法】，又回到了【原始FM算法】。

 

此时原始FM算法的，

n*= len(input*) = p

理想情况下，每个field内只有1个非零值，于是，

p =n_field = n

从而有，

n* =n 

证毕。

 

于是我们知道，在理想情况下，第i个field里面的那个唯一非零值，正是input*中的第i个数，叫它xi也没毛病。

 

而参数数量方面。我们有n个field，就有n个embd层，于是有n个 featuresize*k的参数矩阵。

显然可以做到，对输入的x中的 len(x) 个维度来说，每个维度 xi 都有唯一对应的 vi,shape=(1,k)。

 

这又反过来解释了为什么可以参数共用。

因为提取n个非零项组成input*，再与n个k维的vi相乘，这件事情得到的结果，不正是deep部分dense feature这个层的输出吗？

 

这说明，对我们写代码来说，并没有什么区别，考虑n_field就足够了，不需要关注len(input)。

每次拼好长为n_field的input*向量之后，按照原始的算法，算fm1-fm2就完事了。

综上，n=n_field是有道理的。

 

 

继续，我们要把n个field的vixi全部算出来。

用一个循环就可以了。

import torch
import torch.nn as nn


#对n个field搭建model

n_field = 4                 #有4个字段 
feature_sizes= [5,3,6,4]    #每个字段向量化后的长度分别为5,3,6,4
embedding_size = 30        #希望以k=30来表达这些向量


n_embds = nn.ModuleList(
[nn.Embedding(feature_sizes[i], embedding_size) for i in range(n_fileds)]
)


#从n_field个字段内提取唯一的非零值对应的vixi

#假设有一个存储idx的文件，m个样本在n个field对应的非零项的下标
#shape=(m_samples,n_field)
train_idx = read_from_file('xx.file') 

#再有m个样本在n个field对应的非零项xi的值，shape=(m_samples,n_field)
train_values = read_from_file('xxxxx.file') 

results = []
for i , module in enumerate(n_embds):
    #当前为 i_th_field
    batch_idx = torch.Tensor(train_idx[:,i])         #shape=(m)
    batch_vis = module(batch_idx)                    #shape=(m,k)
    batch_xis = torch.FloatTensor(train_values[:,i]) #shape=(m)

    #我们让每个样本的vi与对应的xi相乘
    res = (batch_vis.t())*train_values    #(k,m)*(m)=(k,m)
    res = res.t()                         #shape=(m,k)
    results.append(res)

#由前面的讨论知道，此时res的每行，
#都是第m个样本在第n个field的(v'x)'=vixi，即长度为k的行向量
#[vi1xi,vi2xi,...,vikxi]

现在我们得到了一个results列表。

需要用它来算FM1和FM2。

 

 

观察公式，对FM1，我们需要固定K不动，先sum一轮vikxi，然后逐项平方。最后逐K累加。

对FM2，我们需要固定K不动，先平方vikxi，再sum。最后逐个K累加。

 

先看FM1，以K为轴，先固定K不动。

(1)以n为维度sum一次。其实就是把results这个 list of tensor里面的每一个shape相同的tensor ，在相同位置上全部加起来。

fm1_step1 = sum(results)    #sum(n*[m,k]) -> (m,k)，此处必须使用python原生sum()

关于为什么要使用原生sum()，请看 《Pytorch Tensor的奇妙运算》 加法部分。

(2)然后逐项平方。

fm1_step2 = fm1_step1*fm1_step1  #(m,k)*(m,k)=(m,k)

(3)最后逐K累加。

fm1 = torch.sum(fm1_step2,dim=1) #sum([m,k] ,dim=1) -> (m)

 

再看FM2，同样以K为轴，先固定K不动。

(1)先进行逐项平方

fm2_step1= [item*item for item in results] #list of n*(m,k)

(2)再以n为维度sum一次。

fm2_step2 = sum(fm2_step1) #sum(n*[m,k]) -> (m,k)，此处必须使用python原生sum()

(3)最后逐K累加。

fm2 = torch.sum(fm2_step2,dim=1)  #sum([m,k],dim=1) -> (m)

 

最后两者相减，乘系数即可。

quadratic_term = (fm1-fm2)*0.5

 

至此，我们得到了 $y=w0+\sum wixi + \sum \sum wij·xixj$ 中的最后一个二次项。

但是还少了线性部分。

这个简单。

linear_part = nn.ModuleList(
[  nn.Linear(feature_sizes[i]),1)  for i in range(n_field)]
)

 

现在FM部分被彻底搞定了，我们看看进度条。

 

5.合并输出，计算loss

import torch.nn.functional as F


#设deep部分的输出为 deep_out
total_out = deep_out + quadratic_term  #shape=(m,1)

#根据任务不同，这里的输出可以做不同的处理。比如点击率预测就是分类问题了。
#但是我当前的需求是数值预测，所以直接拿来用

#随便选一个损失函数，或者自定义
loss_func = F.binary_cross_entropy_with_logits

#优化器
optimizer = torch.optim.SGD(self.parameters(), lr=self.learning_rate, weight_decay=self.weight_decay)
#optimizer = torch.optim.Adam(self.parameters(), lr=self.learning_rate, weight_decay=self.weight_decay)
#optimizer = torch.optim.RMSprop(self.parameters(), lr=self.learning_rate, weight_decay=self.weight_decay)
#optimizer = torch.optim.Adagrad(self.parameters(), lr=self.learning_rate, weight_decay=self.weight_decay)


optimizer.zero_grad()
loss = loss_func(total_out,train_y)
loss.backward()
optimizer.step()

 

 

#补充理解

#关于那个因子分解可以扩大学习面。

#对wij来说，需要样本里面存在xi和xj交叉的情况（两者同时非0出现在同一个样本中），算出来的y去算loss，再反向传播，才能更新到wij。一共有n*n个参数，显然很难满足n*n个wij都被训练到。

#分解之后的vi，只跟xi关联。于是只需要样本里面存在某个xi非0的情况，就可以对这个维度的vi进行更新。

#于是我们只需要最低n个样本，就能照顾到每一种xi非0的情况，就能训练到n个vi。

 

 

#参考

@bitcarmanlee: https://blog.csdn.net/bitcarmanlee/article/details/52143909

site:美团点评 @del2z, 大龙 : 《深入FFM原理与实践》https://tech.meituan.com/2016/03/03/deep-understanding-of-ffm-principles-and-practices.html

site:简书 @石晓文的学习日记 : https://www.jianshu.com/p/6f1c2643d31b

site:知乎 @Jachin: https://zhuanlan.zhihu.com/p/33479030