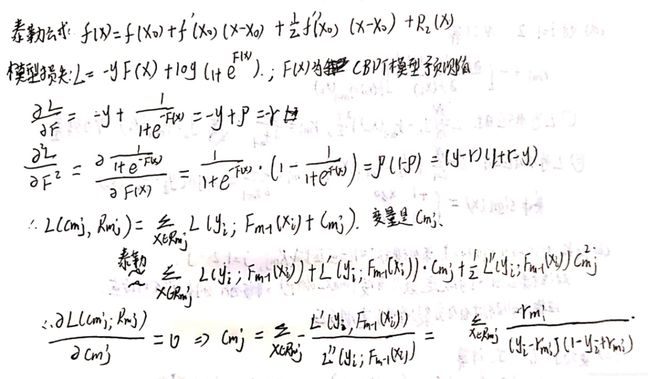梯度提升树(GBDT)原理与Python实现
前言
看完统计学习方法有一段时间了,一直拖着没有总结。临近期末,复习完课程再去学新的知识过于疲劳,就想着把之前决定写的总结都给补一下。统计学习方法实现基本也差不多完成了(还有一两章寒假慢慢补吧),所有代码详见github(包括决策树,逻辑回归,SVM,梯度提升树,Adaboost,隐马尔可夫模型等)。所有实现都有很详细的注释,如果能够帮助到你的话就可以点个赞吧~
正文
回归树
在讲梯度提升树之前,先简单了解下回归树。因为GBDT中每一轮对残差拟合的都是回归树(无论是用GBDT做回归还是分类)。
在CART算法中,回归树均为二叉树,内部节点特征值作为分割点,左边分支对应特征值小于该切分点,右边分支对应特征值大于该切分点。对于每个分支递归的寻找特征值与切分点,最后将输入空间(即特征空间)划分为了有限的单元(也就是叶节点),然后在在每一个单元上给出预测的值作为最终输出。
下面我们思考一下回归树的生成
首先我们有输入变量X与输出变量Y。共同构成训练集D{(x1,y1),(x2,y2)…(xn,yn)}
假定我们已经划分好了一棵树,它将输入空间划分为R1,R2,…,Rm总共m个单元(叶节点)。在每一个单元上预测值为cm。那么回归树可以表示为 f ( x ) = ∑ m = 1 M c m I ( x i ϵ R m ) f(x)=\sum_{m=1}^{M} c_{m}I (x_i \epsilon R_m ) f(x)=m=1∑McmI(xiϵRm)
在每一个叶节点上,我们的损失函数使用MSE(均方误差)来衡量我们预测的准确性,则在该叶节点上损失为 L m = ∑ x ϵ R m ( y i − c m ) 2 L_m=\sum_{x\epsilon Rm}(y_{i}-c_m)^2 Lm=xϵRm∑(yi−cm)2
那么我们怎么获得使得每一个叶节点上的损失最小呢。我们以cm为参数,对损失函数求导,令其为0,即可获得cm最佳值。如果你对于求和符号很不习惯,你可以试试一项一项的写,然后对每一个二次项中的cm求导,所有二次项相加和为0,得到cm即叶节点上所有值的均值。还是做个示范吧
∂ L m ∂ c m = ( y 1 − c m ) + ( y 2 − c m ) + . . . + ( y n − c m ) = 0 \frac{\partial L_m}{\partial c_m}=(y_1-c_m)+(y_2-c_m)+...+(y_n-c_m)=0 ∂cm∂Lm=(y1−cm)+(y2−cm)+...+(yn−cm)=0
即 c m = a v g ( y i ∣ x i ϵ R m ) c_m=avg(y_i|x_i\epsilon R_m) cm=avg(yi∣xiϵRm)
当我们获得了叶节点,基于以上我们就知道了如何获取最佳预测值了。那么下面的任务就是如何对于对输入空间进行划分呢。
我们采用启发式的划分法,遍历所有可能的划分特征以及每一个特征对应的值,尝试以该值作为切分点构建左右节点。注意,回归树的分裂准则也是MSE。那么,我们就只需要找到划分之后似的左右节点MSE之和最小的特征与特征值作为切分变量(split variable)与切分点(split point)。假设当前选取第j个变量与其取值s,则左右区域R1与R2为: R 1 ( j , s ) = ( x ∣ x ( j ) < = s ) R_{1(j,s)}= (x|x^{(j)}<=s) R1(j,s)=(x∣x(j)<=s), R 2 ( j , s ) = ( x ∣ x ( j ) > s ) R_{2(j,s)}= (x|x^{(j)}>s) R2(j,s)=(x∣x(j)>s)
则我们遍历所有切分特征与切分点,求解
min j , s [ min c 1 ∑ x i ∈ R 1 ( j , s ) ( y i − c 1 ) 2 + min c 2 ∑ x i ∈ R 2 ( j , s ) ( y i − c 2 ) 2 ] \min _{j, s}\left[\min _{c_{1}} \sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-c_{1}\right)^{2}+\min _{c_{2}} \sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-c_{2}\right)^{2}\right] j,smin⎣⎡c1minxi∈R1(j,s)∑(yi−c1)2+c2minxi∈R2(j,s)∑(yi−c2)2⎦⎤
从而获得最解切分变量与切分点。其中,确定切分之后,c1,c2的值为
c 1 = a v g ( y i ∣ x i ϵ R 1 ( j , s ) ) ) c1=avg(yi|xi\epsilon R_{1(j,s))}) c1=avg(yi∣xiϵR1(j,s)))
c 2 = a v g ( y i ∣ x i ϵ R 2 ( j , s ) ) ) c2=avg(yi|xi\epsilon R_{2(j,s))}) c2=avg(yi∣xiϵR2(j,s)))
最小二乘回归树生成算法
回归提升树
在进入正题之前,再简单说说回归提升树。提升树模型使用的前向分步算法,模型是决策树的加法模型。首先确定初始提升树 f 0 ( x ) = 0 f_0(x)=0 f0(x)=0。则在第m步的时候,模型就是 f m ( x ) = f m − 1 ( x ) + T ( x ; θ m ) f_m(x)=f_{m-1}(x)+T(x; \theta_m) fm(x)=fm−1(x)+T(x;θm)
其中 T ( X , θ m ) T(X,\theta_m) T(X,θm)就是我们第m步需要构建的回归树,即
T ( x ; θ m ) = ∑ m = 1 M c m I ( x i ϵ R m ) T(x; \theta_m)=\sum_{m=1}^{M} c_{m}I (x_i \epsilon R_m ) T(x;θm)=m=1∑McmI(xiϵRm)
Rm是我们将输入空间划分为的m个单元(叶节点)Cm是每一个单元的预测值。而 θ m \theta_m θm是我们需要求解的这颗回归树的参数。那么我们如何求解 θ m \theta_m θm得到这棵树呢。
我们损失函数使用MSE: L ( y , f ( x ) ) = ( y − f ( x ) ) 2 L(y,f(x))=(y-f(x))^2 L(y,f(x))=(y−f(x))2
那么在第m轮的时候,损失就是:
L ( y , f m − 1 ( x ) + T ( x ; θ m ) ) = [ y − f m − 1 ( x ) − T ( x ; θ m ) ] 2 = [ r − T ( x ; θ m ) ] 2 L(y,f_{m-1}(x)+T(x; \theta_m)) \\ =[y-f_{m-1}(x)-T(x; \theta_m)]^2\\=[r-T(x; \theta_m)]^2 L(y,fm−1(x)+T(x;θm))=[y−fm−1(x)−T(x;θm)]2=[r−T(x;θm)]2
其中 r = y − f m − 1 ( x ) r=y-f_{m-1}(x) r=y−fm−1(x)是当前模型拟合数据的残差。所以每一轮我们构建的回归树只需要对当前模型的残差值进行拟合即可。
了解了回归提升树,我们可以进入正题了。
GBDT
在上面的回归提升树中,我们每一轮都是拟合的模型残差,而在梯度提升树中(他名字都有梯度了嘛),我们使用损失函数负梯度(负梯度具有最速下降性)作为当前模型的残差的近似值。那么我们的回归树拟合的就是当前模型的负梯度。即:
r m i ~ = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) , i = 1 , 2 , … N \widetilde{r_{mi}}=-\left[\frac{\partial L\left(y_{i}, F\left(x_{i}\right)\right)}{\partial F\left(x_{i}\right)}\right]_{F(x)=F_{m-1}(x)}, i=1,2, \ldots N rmi =−[∂F(xi)∂L(yi,F(xi))]F(x)=Fm−1(x),i=1,2,…N
下面就可以给出GBDT算法的过程了。
由于里面的损失函数求梯度与叶子结点求解最优值有一些推导过程,手打公式有些麻烦,就手写一下。
用于回归
GBDT用于回归算法步骤如下:
- 初始化 f x ( x ) = a r g m i n c ∑ i = 1 n L ( y i ; c ) f_x(x)=argmin_c \sum_{i=1}^{n} L(y_i;c) fx(x)=argminc∑i=1nL(yi;c)。其中c就是我们对所有节点的初始预测值。当我们使用不同的损失函数时,有不同的初始值。在回归问题中,我们损失函数一般可以使用MSE,MAE(绝对值误差)。当然你可以自己定义一个损失函数,有一阶导即可。使用MSE时, c = a v e r a g e ( y ) c=average(y) c=average(y)。使用MAE时, c = m i d ( y ) c=mid(y) c=mid(y)。下面推导一下使用以上两种损失函数时出初始化值为多少。

- 对m=1,2…,M(M轮迭代,产生M棵树)
(a) 对I=1,2…N ,即每个样本,计算:
r m i ~ = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) , i = 1 , 2 , … N \widetilde{r_{mi}}=-\left[\frac{\partial L\left(y_{i}, F\left(x_{i}\right)\right)}{\partial F\left(x_{i}\right)}\right]_{F(x)=F_{m-1}(x)}, i=1,2, \ldots N rmi =−[∂F(xi)∂L(yi,F(xi))]F(x)=Fm−1(x),i=1,2,…N
下面是使用MSE,与MAE时,残差近似值推导

(b)对 r m i r_{mi} rmi拟合一颗回归树,第m棵树的叶节点区域为 R m j , j = 1 , 2 , . . . , J R_{mj},j=1,2,...,J Rmj,j=1,2,...,J
对该回归树可以设定最大深度(max_deep),树的深度为h,则有2^h个节点。
注意,无论损失函数是什么,回归树的分裂准则是MSE
©对j=1,2…J,即每个叶节点Rmj,计算其预测值:
c m j = a r g m i n c ∑ x ϵ R m j L ( y i ; f m − 1 ( x ) + c ) c_{mj}=argmin_c \sum_{x\epsilon R_{mj}}L(y_i;f_{m-1}(x)+c) cmj=argmincxϵRmj∑L(yi;fm−1(x)+c) Cmj值的推导:
(d) 更新
f m ( x ) = f m − 1 ( x ) + ∑ j = 1 J c m j I ( x ϵ R m j ) f_m(x)=f_{m-1}(x)+ \sum_{j=1}^J c_{mj}I(x \epsilon R_{mj} ) fm(x)=fm−1(x)+j=1∑JcmjI(xϵRmj)
此外,为了防止树模型过拟合,我们可以对每一棵回归树前面加上一个正则化系数 α m \alpha_m αm,最后公式为 f m ( x ) = f m − 1 ( x ) + α m ∑ j = 1 J c m j I ( x ϵ R m j ) f_m(x)=f_{m-1}(x)+ \alpha_m \sum_{j=1}^J c_{mj}I(x \epsilon R_{mj} ) fm(x)=fm−1(x)+αmj=1∑JcmjI(xϵRmj)
(3)最后一步,得到GBDT模型为: f m ( x ) = f 0 ( x ) + ∑ m = 1 M ∑ j = 1 J α m c m j I ( x ϵ R m j ) f_m(x)=f_{0}(x)+ \sum_{m=1}^M\sum_{j=1}^J\alpha_m c_{mj}I(x \epsilon R_{mj} ) fm(x)=f0(x)+m=1∑Mj=1∑JαmcmjI(xϵRmj)
用于二分类
以下是针对于0-1分类问题,与-1,1分类再构建损失函数上有一点点区别。
首先模型仍然是基于回归树的加法模型 f m ( x ) f_m(x) fm(x)。我们预测样本为正类的记录为 p = 1 1 + e − f m ( x ) p=\frac1 {1+e^{-f_m(x)}} p=1+e−fm(x)1 (类似于逻辑回归)。则预测为负类的概率为 1 − p = 1 1 + e f m ( x ) 1-p=\frac1 {1+e^{f_m(x)}} 1−p=1+efm(x)1
那么损失函数我们使用对数损失函数(LogLoss),则 L = ( y , p ) = − ( y l o g p + ( 1 − y ) l o g ( 1 − p ) ) L=(y,p)=-(ylogp+(1-y)log(1-p)) L=(y,p)=−(ylogp+(1−y)log(1−p))(由极大似然也可推出)。
将 p = 1 1 + e − f m ( x ) p=\frac1 {1+e^{-f_m(x)}} p=1+e−fm(x)1 带入并且化简之后,可以得到 L = − y ∗ f m ( x ) + l o g ( 1 + e f m ( x ) ) L=-y*f_m(x)+log(1+e^{f_m(x)}) L=−y∗fm(x)+log(1+efm(x))
类似的给出算法的流程:
-
初始化 f x ( x ) = a r g m i n c ∑ i = 1 n L ( y i ; c ) f_x(x)=argmin_c \sum_{i=1}^{n} L(y_i;c) fx(x)=argminc∑i=1nL(yi;c)。
将c带入损失函数求导为0,我们可以得到c的初始值为 c = l o g ( ∑ i = 1 n y i ∑ i = 1 n ( 1 − y i ) ) c=log(\frac{\sum_{i=1}^ny_i}{\sum_{i=1}^n(1-y_i)}) c=log(∑i=1n(1−yi)∑i=1nyi)注意,c就是我们初始时对所有节点的初始预测值
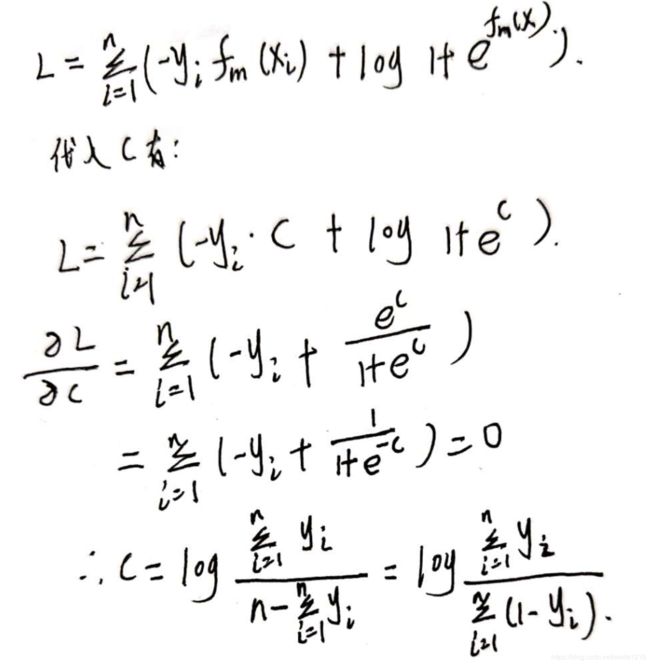
-
对m=1,2…,M(M轮迭代,产生M棵树)
(a) 对I=1,2…N ,即每个样本,计算:
r m i ~ = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) , i = 1 , 2 , … N \widetilde{r_{mi}}=-\left[\frac{\partial L\left(y_{i}, F\left(x_{i}\right)\right)}{\partial F\left(x_{i}\right)}\right]_{F(x)=F_{m-1}(x)}, i=1,2, \ldots N rmi =−[∂F(xi)∂L(yi,F(xi))]F(x)=Fm−1(x),i=1,2,…N
r m i = y i − p r_{mi}=y_i-p rmi=yi−p
其实也就是我们预测的残差。计算如下: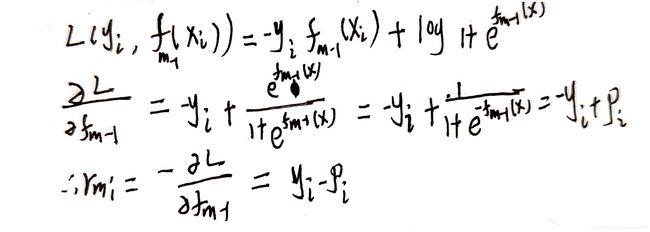
(b)对 r m i r_{mi} rmi拟合一颗回归树,第m棵树的叶节点区域为 R m j , j = 1 , 2 , . . . , J R_{mj},j=1,2,...,J Rmj,j=1,2,...,J
对该回归树可以设定最大深度(max_deep),树的深度为h,则有2^h个节点。
注意,无论损失函数是什么,回归树的分裂准则是MSE(c)对j=1,2…J,即每个叶节点Rmj,计算其预测值:
c m j = a r g m i n c ∑ x ϵ R m j L ( y i ; f m − 1 ( x ) + c ) c_{mj}=argmin_c \sum_{x\epsilon R_{mj}}L(y_i;f_{m-1}(x)+c) cmj=argmincxϵRmj∑L(yi;fm−1(x)+c)
最后可算出Cmj值为:
c m j = ∑ x i ϵ R m j r m i ∑ x i ϵ R m j ( y i − r m i ) ( 1 − y i + r m i ) c_{mj}=\frac{\sum_{x_i \epsilon R_{mj}} r_{mi}}{\sum_{x_i \epsilon R_{mj}}(y_i-r_{mi})(1-y_i+r_{mi})} cmj=∑xiϵRmj(yi−rmi)(1−yi+rmi)∑xiϵRmjrmi
Cmj值的推导比较复杂,求导之后无法直接分离出Cmj,需要使用泰勒展开算的近似值。在最后补上推导。(d) 更新模型
f m ( x ) = f m − 1 ( x ) + ∑ j = 1 J c m j I ( x ϵ R m j ) f_m(x)=f_{m-1}(x)+ \sum_{j=1}^J c_{mj}I(x \epsilon R_{mj} ) fm(x)=fm−1(x)+j=1∑JcmjI(xϵRmj)
此外,为了防止树模型过拟合,我们可以对每一棵回归树前面加上一个正则化系数 α m \alpha_m αm,最后公式为 f m ( x ) = f m − 1 ( x ) + α m ∑ j = 1 J c m j I ( x ϵ R m j ) f_m(x)=f_{m-1}(x)+ \alpha_m \sum_{j=1}^J c_{mj}I(x \epsilon R_{mj} ) fm(x)=fm−1(x)+αmj=1∑JcmjI(xϵRmj)
(3)最后一步,得到GBDT模型为: f m ( x ) = f 0 ( x ) + ∑ m = 1 M ∑ j = 1 J α m c m j I ( x ϵ R m j ) f_m(x)=f_{0}(x)+ \sum_{m=1}^M\sum_{j=1}^J\alpha_m c_{mj}I(x \epsilon R_{mj} ) fm(x)=f0(x)+m=1∑Mj=1∑JαmcmjI(xϵRmj)
以上就是GBDT用于回归和二分类的流程,可以发现两者也都十分类似,GBDT是以当前模型的负梯度值作为残差的近似值拟合,当我们在回归中损失函数使用MSE,在二分类中使用LogLoss的时候,模型的负梯度值就是残差值。
GBDT回归预测实现
使用GBDT对sklearn.datasets中的波士顿房价数据集进行回归预测。模型损失函数使用均方误差,回归树分裂准则也是均方误差。
关于变量的切分,对于离散数据使用的精确切分,即遍历每一个可能的取值点。
对于连续变量,使用近似算法,对所有特征进行排序,选取十分位点进行切割。
下面是三分位数切割实例:

算法的其他实现细节都在注释中
"""
@File : GBDT.py
@Time : 2019-12-20 14:09
@Author : Lee
@Software: PyCharm
@Email: [email protected]
"""
import pandas as pd
import numpy as np
# 样本 boston_house_price
# 对数据集的说明:
# CRIM:城镇人均犯罪率。
# ZN:住宅用地超过 25000 sq.ft. 的比例。
# INDUS:城镇非零售商用土地的比例。
# CHAS:查理斯河空变量(如果边界是河流,则为1;否则为0)。
# NOX:一氧化氮浓度。
# RM:住宅平均房间数。
# AGE:1940 年之前建成的自用房屋比例。
# DIS:到波士顿五个中心区域的加权距离。
# RAD:辐射性公路的接近指数。
# TAX:每 10000 美元的全值财产税率。
# PTRATIO:城镇师生比例。
# B:1000(Bk-0.63)^ 2,其中 Bk 指代城镇中黑人的比例。
# LSTAT:人口中地位低下者的比例。
# MEDV:自住房的平均房价,以千美元计。
# 测试结果
# 以百分之20误差率以内作为一次良好的预测
# 测试准确率80%左右
# R2_score(相关系数的平方)在0.7左右(不是很稳定,因为样本数量较小,测试数据在100条左右)
# 调整迭代轮数(树的数量)以及树的深度(max_deep),以及对残差拟合回归树的正则化系数(alpha)都会有不同的影响
def loaddata(filename):
data=pd.read_csv(filename)
#打乱数据集
from sklearn.utils import shuffle
data = shuffle(data)
# 你也可以设置种子保证结果的一致
# data = shuffle(data,random_state=666)
# 切分样本,作为训练集和测试集
rate=0.2
data=data.values
train_data=data[:int(len(data)*(1-rate)),:]
test_data=data[int(len(data)*(1-rate)):,:]
return train_data,test_data
def findBestFeatureAndPoint(node):
'''
依据MSE准则,找到最佳切分特征和最佳切分点
:param node: 进行分裂的节点, 一个矩阵
:return: 切分特征与切分点
'''
# n为特征数
m,n=node.shape
# 因为最后一列是标签值
n=n-1
# 需要预测的真实值
y = node[:, -1]
# 用来保存最佳切分特征与切分点
# 以及左右子树
min_loss = np.Inf
best_feature = -1
best_point = -1
best_left=None
best_right=None
# 找到最佳切分特征与切分点
# 我们遍历所有特征,然后遍历该特征所有(或者部分)切分点
# 取决于该特征是离散还是连续变量
for feature in range(n):
# 注意是n-1 , 因为最后一个是样本需要预测的值
# 获得进行切分列
# 因为是连续数据,有可能有很多不同的值
# 所以此处我们进行切分的时候,若是离散数据(默认种类小于等于10),我们进行精确切分
# 若类型大于10,认为是连续变量,进行10分位点切分
column=node[:,feature]
category=sorted(set(column))
if len(category)<=10:
split_point=category
else:
# 使用np.arrange来每次找到1/10数据点所在的索引
# 然后进行切分
split_point = np.arange(0, len(category), len(category) // 10)
split_point = [category[split_point[i]] for i in range(0, len(split_point))]
# 确定了所有切分点之后,对切分点进行遍历,找到最佳切分点
for point in split_point:
# 尝试切分
left=column[column<=point]
right=column[column>point]
# 左右两边的需要预测的真实值
y_left=y[column<=point]
y_right=y[column>point]
# 计算左右两边最佳的Cmj
# cart回归树损失函数为MSE
# 所以我们只需要取节点上的均值即可
c_left = np.average(y_left)
c_right = np.average(y_right)
loss=np.sum(np.square(y_left-c_left))+np.sum(np.square(y_right-c_right))
if loss<min_loss:
min_loss=loss
best_feature=feature
best_point=point
best_left=node[column<=point]
best_right=node[column>point]
return (best_feature,best_point,best_left,best_right)
def createCART(data,deep,max_deep=2):
'''
创建回归树,分裂准则MSE(最小均方误差)
:param deep: 树的当前深度
:param max_deep: 树的最大深度(从0开始),默认为2,即产生4个叶子节点
:param data: 训练样本,其中data中的最后一列值为上一轮训练之后的残差
:return: 一颗回归树
'''
# 树的结构例如
# tree={3:{'left':{4:{'left':23.1,'right':19.6},'point':0},'right':{6:{'left':23.1,'right':19.6},'point':4.5}},'point':10.4}
# 上面是一颗2层的回归树
# 3代表根节点以第三个特征进行分类,分裂的切分点是point=10.4
# 然后是左右子树left,right
# left也是一个字典,对应左子树
# 4代表左子树以特征四为分裂特征,切分点是point=0
# 分裂之后的left仍然是一个字典,其中有left和right对应着23.1,19.6
# 这两个值即为我们的预测值
# 右子树也同理
if deep<=max_deep:
feature,point,left,right=findBestFeatureAndPoint(data)
tree = {feature: {}}
if deep!=max_deep:
# 不是最后一层,继续生成树
tree['point']=point
if len(left)>=2:
# 必须要保证样本长度大于1,才能分裂
tree[feature]['left']=createCART(left,deep+1,max_deep)
else:
tree[feature]['left']=np.average(left)
if len(right)>=2:
tree[feature]['right']=createCART(right,deep+1,max_deep)
else:
tree[feature]['right']=np.average(right)
else:
# feature, point, left, right = findBestFeatureAndPoint(data)
# tree['point']=point
# # y标签在训练样本最后一列,用-1获取
# y_left=left[:,-1]
# y_right=right[:,-1]
# c_left = np.average(y_left)
# c_right = np.average(y_right)
# 最后一层树,保存叶节点的值
return np.average(data[:,-1])
return tree
def gradientBoosting(round, data, alpha):
'''
:param round: 迭代论数,也就是树的个数
:param data: 训练集
:param alpha: 防止过拟合,每一棵树的正则化系数
:return:
'''
tree_list=[]
# 第一步,初始化fx0,即找到使得损失函数最小的c
# 即所有样本点的均值
# -1 代表没有切分特征,所有值均预测为样本点均值
fx0={-1:np.average(data[:,-1])}
tree_list.append(fx0)
# 开始迭代训练,对每一轮的残差拟合回归树
for i in range(1,round):
# 更新样本值,rmi=yi-fmx
# TODO:没有想到更新残差较好的方式
# 目前想到的就是对每一个样本以当前的提升树进行一次预测
# 然后获得预测值与真实值进行相减,将样本真实值变为残差
# 如果你碰巧看到了,有好的想法,欢迎与我交流~
if i==1:
data[:,-1]=data[:,-1]-fx0[-1]
else:
for i in range(len(data)):
# 注意,这里穿的列表是tree_list中最后一个
# 因为我们只需要对残差进行拟合,data[:,-1]每一轮都进行了更新,所以我们只要减去上一颗提升树的预测结果就是残差了
data[i, -1] = data[i, -1] - predict_for_rm(data[i], tree_list[-1], alpha)
# 上面已经将样本值变为了残差,下面对残差拟合一颗回归树
fx = createCART(data, deep=0, max_deep=4)
#
# 将树添加到列表
tree_list.append(fx)
return tree_list
def predict_for_rm(data, tree, alpha):
'''
获得前一轮 第m-1颗树 的预测值,从而获得残差
:param data: 一条样本
:param tree: 第 m-1 颗树
:param alpha: 正则化系数
:return: 第m-1颗树预测的值
'''
while True:
# 遍历该棵树,直到叶节点
# 叶节点与子树的区别在于一节点上的值为float
# 而子树是一个字典,有point键,用作切分点
# tree={3:{'left':{4:{'left':23.1,'right':19.6},'point':0},'right':{6:{'left':23.1,'right':19.6},'point':4.5}},'point':10.4}
#
if type(tree).__name__=='dict':
# 如果是字典,那么这是一颗子树,
point = tree['point']
# tree.keys()=dict_keys([3, 'point'])
# 所以int值对应的是特征,但是字典的键值是无序的,我们无法保证第一个是特征,所以用类型来判断
feature = list(tree.keys())[0] if type(list(tree.keys())[0]).__name__ == 'int' else list(tree.keys())[1]
if data[feature] <= point:
tree = tree[feature]['left']
else:
tree = tree[feature]['right']
else:
# 当tree中没有切分点point,证明这是一个叶节点,tree就是预测值,返回获得预测值
return alpha * tree
def predict(data, tree_list, alpha):
'''
对一条样本进行预测
:param tree_list: 所有树的列表
:param data: 一条需要预测的样本点
:param alpha:正则化系数
:return: 预测值
'''
m=len(tree_list)
fmx=0
for i in range(m):
tree=tree_list[i]
if i==0:
# fx0={-1:np.average(data[:,-1])}
# fx0是一个叶节点,只有一个预测值,树的深度为0
fmx+=tree[-1]
else:
while True:
# 遍历该棵树,直到叶节点
# 叶节点与子树的区别在于一节点上的值为float
# 而子树是一个字典,有point键,用作切分点
# tree={3:{'left':{4:{'left':23.1,'right':19.6},'point':0},'right':{6:{'left':23.1,'right':19.6},'point':4.5}},'point':10.4}
#
if type(tree).__name__=='dict':
# 如果是字典,那么这是一颗子树,
point=tree['point']
# tree.keys()=dict_keys([3, 'point'])
# 所以int值对应的是特征,但是字典的键值是无序的,我们无法保证第一个是特征,所以用类型来判断
feature=list(tree.keys())[0] if type(list(tree.keys())[0]).__name__=='int' else list(tree.keys())[1]
if data[feature]<=point:
tree=tree[feature]['left']
else:
tree=tree[feature]['right']
else:
# 当tree中没有切分点point,证明这是一个叶节点,tree就是预测值,返回获得预测值
fmx+= alpha * tree
break
return fmx
def test(X_test, y_test, tree_list, alpha):
acc = 0 # 正确率
acc_num = 0 # 正确个数
y_predict=[]
for i in range(len(X_test)):
print('testing ***', i)
x = X_test[i]
y_pred =predict(x, tree_list, alpha)
y_predict.append(y_pred)
if y_pred/y_test[i]<1.25 and y_pred/y_test[i]>0.8:
acc_num += 1
print(f'testing {i}th data :y_pred={y_pred},y={y_test[i]}')
print('now_acc=', acc_num / (i + 1))
return y_predict
if __name__=='__main__':
train_data,test_data=loaddata('boston_house_prices.csv')
tree_list=gradientBoosting(10,train_data,0.12)
X_test,y_test=test_data[:,:-1],test_data[:,-1]
y_pred=test(X_test,y_test,tree_list,0.12)
from sklearn.metrics import r2_score
score = r2_score(y_test, y_pred)
print(score)