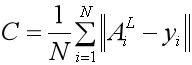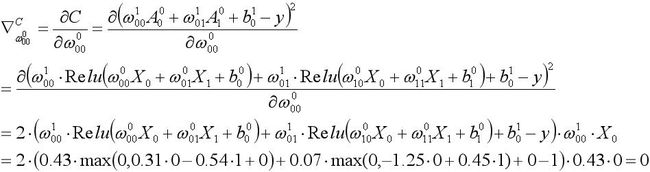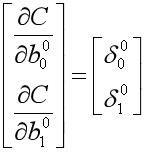Deeplearning4j源码研习(1): BP算法原理及源码实现

Eclipse Deeplearning4j GitChat课程：https://gitbook.cn/gitchat/column/5bfb6741ae0e5f436e35cd9f
Eclipse Deeplearning4j 系列博客：https://blog.csdn.net/wangongxi
Eclipse Deeplearning4j Github：https://github.com/eclipse/deeplearning4j

对于神经网络来讲，训练的过程是在更新网络权重和偏重的值，采取的方法有梯度下降、牛顿法等。由于深度学习通常有较多的网络层数，参数较多，而且二阶的优化算法本身就非常消耗内存，因此，实际应用中，梯度下降运用较多。梯度下降更新模型参数的公式：

 

式子中的代表网络中的某一个需要训练的权重参数，K代表第K次迭代，代表学习率/步长。注意，每一层网络的参数的学习率可以不同。表示损失函数对该权重的梯度。注意，该公式不带任何正则化项和诸如ADAM等带有动量的更新策略，是原始梯度下降的写法，在下面的例子中，也采用该标准形式。

对于该公式，每次迭代前的权重值和学习率都是确定的（学习率一般可以固定，作为人工设定的超参数之一）。而梯度的计算通常依赖于误差反向传播的思想，即BP算法。需要澄清的是，BP算法并非是更新网络权重的直接算法，而是提供了计算梯度的一种策略。这一点，在Goodfellow《Deep Learning》一书中的第6章中有更为明确的描述。有兴趣的同学可以参考相关内容。就个人理解而言，BP算法是希望每一次迭代时的输出结果和期望结果误差的值可以直接作用于权重的更新。虽然在某个具体的问题上，这个误差的大小由损失函数的形式和学习率等多种因素共同决定，但可以在权重更新中有所体现或者说产生一定的影响非常重要。从纯粹计算的角度来看，神经网络可以认为是一个复合函数。在定义好损失函数后，梯度就可以基于链式法则进行求导计算。在此基础上，就可以完成一次权重的迭代更新。因此也有很多观点认为，反向传播的核心就是链式法则。这里不讨论BP的核心思想，下面就结合XOR的例子来给出BP算法的整个计算过程，并且以此为例来分析Deeplearning4j的源码实现。

XOR问题源于一种可以进行异或计算的门电路。其输入输出的对应关系可见下图：

 

X1	X2	Y
0	0	0
0	1	1
1	0	1
1	1	0

 

从机器学习的角度看，X1和X2表示两个特征，Y表示标注。我们可以用分类或者回归的思想来解决XOR问题。这篇博客采用的是回归的方法。为了简化后面公式的推导，我们构建一个只含有一层隐藏层的神经网络。如果用Deeplearning4j建模，则代码如下：

 

 

        int seed = 1234567;
        int iterations = 1;
        MultiLayerConfiguration conf = new NeuralNetConfiguration.Builder()
                                .seed(seed)
                                .iterations(iterations)
                                .learningRate(0.01)
                                .miniBatch(false)
                                .useDropConnect(false)
                                .weightInit(WeightInit.XAVIER)
                                .optimizationAlgo(OptimizationAlgorithm.STOCHASTIC_GRADIENT_DESCENT)
                                .updater(Updater.SGD)
                                .list()
                                .layer(0, new DenseLayer.Builder()
                                                        .nIn(2)
                                                        .nOut(2)
                                                        .activation(Activation.RELU)//Activation.IDENTITY will not work
                                                                                    //since non-linear transformation
                                                                                    //is needed here
                                                        .learningRate(0.01)
                                                        .build())
                                .layer(1, new OutputLayer.Builder(LossFunctions.LossFunction.MSE)
                                                         .activation(Activation.IDENTITY)
                                                         .learningRate(0.01)
                                                         .nIn(2).nOut(1).build())
                                .backprop(true).pretrain(false)
                                .build();
        MultiLayerNetwork model = new MultiLayerNetwork(conf);
        model.init();      

损失函数我们使用的是回归问题常用的均方误差函数（Mean Square Error，MSE）。

在Deeplearning4j中，MSE的定义如下：。

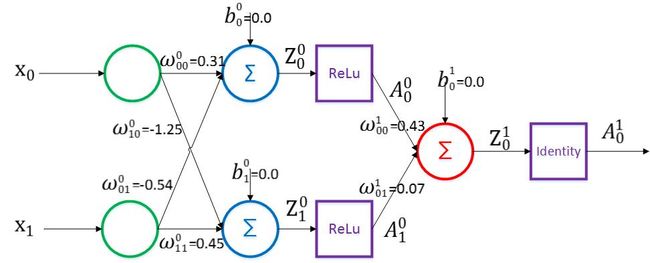
其中N是输出层的维度。优化算法使用的是随机梯度下降（SGD），同时为了方便后面公式的推导，我们这里不使用mini-batch来计算梯度，而是用标准的随机梯度下降，即利用单条训练数据来更新权重。每一层的学习率设为0.01。隐藏层的激励函数使用RELU。需要注意的是，随机种子用于初始化权重，固定的种子可以保证每次初始化的权重相同。当然纯粹看代码还未必直观，下面就直接利用Visio绘出相应的神经网络结构图以及初始化后的权重。

图中的各个组件简单做下说明：

绿色圆圈：输入层神经元

蓝色圆圈：隐藏层神经元

红色圆圈：输出层神经元

紫色方框：激励函数/非线性变换函数

黑色带前向箭头的线：神经元间的连接

 

从图中看出，一共有9个参数需要训练，其中6个是权重值，另外3个是偏置。我们可以直接调用Deeplearning4j中summary接口来获取神经网络的参数信息：

 

============================================================================================================================================
LayerName (LayerType)                   nIn,nOut       TotalParams    ParamsShape                   
============================================================================================================================================
0 (DenseLayer)                          2,2            6              b:{1,2}, W:{2,2}              
1 (OutputLayer)                         2,1            3              b:{1,1}, W:{2,1}              
--------------------------------------------------------------------------------------------------------------------------------------------
            Total Parameters:  9
        Trainable Parameters:  9
           Frozen Parameters:  0
============================================================================================================================================

 

可以发现通过接口获取的模型参数信息和我们之前说明的是一致的。

为了方便后续公式的推导，将公式进行进一步展开

这里以更新权重、和为例来解释BP算法。

根据之前的描述，利用SGD进行权重更新的时候，需要计算损失函数对于每个权重的梯度。对于，我们需要计算以下公式（当前输入=0,=1）：

即梯度计算的结果为-0.87165

根据梯度下降更新权重的公式，经过本次迭代后被更新为：

类似的，b10的权重更新如下：

我们用Deeplearning4j已经搭建好的模型来验证下我们的计算结果：

 

Before Fit Model Param: 
0_W,[[0.31, -1.25],
 [-0.54, 0.45]]
0_b,[0.00, 0.00]
1_W,[0.43, 0.07]
1_b,0.00
Iter Training Finish: 0
Feature: [0.00, 0.00]
0_W,[[0.31, -1.25],
 [-0.54, 0.45]]
0_b,[0.00, 0.00]
1_W,[0.43, 0.07]
1_b,0.00
Iter Training Finish: 1
Feature: [0.00, 1.00]
0_W,[[0.31, -1.25],
 [-0.54, 0.45]]
0_b,[0.00, 0.00]
1_W,[0.43, 0.08]
1_b,0.02

需要说明的是，第一次迭代两个输入都为0，所以权重没有改变。我们刚才的公式推导实际是第二次迭代后的结果。我们看第二次迭代的时候，即输入分别是0和1的时候，也就是日志中的1_W中的第二个数值发生了变化，0.07-->0.08。这和我们的手工计算结果0.0787是吻合的。而对于，也就是日志中的1_b，从0.00-->0.02和我们计算的结果0.019也是吻合的。由此通过运行程序来验证我们之前的推导。
最后推导一下的更新过程。

的推导略微复杂些，其中还包括了对Relu函数的求导。但由于的输入值是0，所以本次迭代的值不发生改变。这个从上面我们日志的信息中也可以验证。

通过将中间变量不断展开的方式来计算损失函数对于每个权重变量偏导数的方式虽然比较直观，但在实际编码的时候，我们希望通过张量的形式来落地。我们不妨将这9个变量梯度的计算形式基于链式法则都写出来，这样可以从中发现一些规律：

为了方便下面源码的实现，我们将部分求导的中间结果重新定义：

1.：残差，可以认为是在没有进行非线性变换前各层输出值对误差的敏感程度

2.：残差计算可以重复利用的中间结果。

注意，公式中的用大圆黑点表示的是Hadmard乘积，即对应元素相乘。

我们把求取梯度的结果用张量形式表示：

对于输出层的权重

对于隐藏层的权重和偏置

在明确了损失函数对于每一个权重和偏置的梯度之后，结合学习率以及迭代前各个变量的值就可以计算出迭代的结果。到此我们完成了对XOR问题一次迭代的手工计算以及计算形式的张量化。在此我们做下小结：神经网络基于BP算法将误差由输出层反向传播，通过计算损失函数对于权重和偏置的梯度并结合学习率等固定的超参数，在随机梯度下降算法的基础上，进行一次权重的更新迭代。这就是BP算法的大致流程。下面就以上XOR的例子，我们来看下Deeplearning4j底层的源码实现。

首先我们给出一次迭代的算法过程描述：

(1). 根据用户设置的参数判断是否进行BP算法。若是进入(2)，否则退出
(2) 根据用户参数选择优化器（本例中是SGD）以及获取用户设置的迭代次数。若尚未完成全部迭代，则进入(3)，否则进入(4)
(3). 计算梯度以及损失函数的值
      (a).计算输出层的输入张量
      (b).基于BP算法计算输出层各权重、偏置的梯度、残差以及后一层的值。
      (c).从倒数第二层开始至倒数第一层，根据前一层计算的的值计算当前层的梯度和残差以及以及后一层的值
      (d).循环操作步骤(c)直至结束
      (e).计算损失函数的值
(4). 根据(3)中计算的所有梯度值，结合超参数学习率、更新机制等对所有权重和偏置进行更新

在以上描述的计算流程中，部分的逻辑用以下时序图来表示：

最后，我挑选一些主要的源码片段来做下说明：

1.MultiLayerNetwork.fit

 

    public void fit(INDArray features, INDArray labels, INDArray featuresMask, INDArray labelsMask) {
        setInput(features);  // 设置训练数据
        setLabels(labels);   //设置训练标注
        if (featuresMask != null || labelsMask != null) {
            this.setLayerMaskArrays(featuresMask, labelsMask);
        }
        update(TaskUtils.buildTask(features, labels));

        if (layerWiseConfigurations.isPretrain()) {
            pretrain(features);
        }

        if (layerWiseConfigurations.isBackprop()) {  //根据用户设置的参数判断是否要进行BP反向传播算法
            if (layerWiseConfigurations.getBackpropType() == BackpropType.TruncatedBPTT) {
                doTruncatedBPTT(features, labels, featuresMask, labelsMask);
            } else {   
                if (solver == null) {   //获取优化器
                    solver = new Solver.Builder().configure(conf()).listeners(getListeners()).model(this).build();
                }

                solver.optimize();    //模型训练/优化
            }
        }

        if (featuresMask != null || labelsMask != null) {
            clearLayerMaskArrays();
        }
    }

这一部分代码是上面算法流程(1)和(2)中的逻辑。其中有一些关于掩码（maskArray）的判断，这里可以先跳过。由于我们设置的优化器是SGD，所以下面会进入StochasticGradientDescent这个类中的optimize方法。顾名思义，就是进行模型的优化了。具体看下面的代码

 

2.StochasticGradientDescent.optimize，SGD优化器的优化方法

 

    public boolean optimize() {
        for (int i = 0; i < conf.getNumIterations(); i++) {

            Pair pair = gradientAndScore();  //计算梯度和损失函数的值
            Gradient gradient = pair.getFirst();

            INDArray params = model.params();
            stepFunction.step(params, gradient.gradient());   //更新参数
            //Note: model.params() is always in-place for MultiLayerNetwork and ComputationGraph, hence no setParams is necessary there
            //However: for pretrain layers, params are NOT a view. Thus a setParams call is necessary
            //But setParams should be a no-op for MLN and CG
            model.setParams(params);  //重置模型参数

            int iterationCount = BaseOptimizer.getIterationCount(model);
            for (IterationListener listener : iterationListeners)
                listener.iterationDone(model, iterationCount);

            checkTerminalConditions(pair.getFirst().gradient(), oldScore, score, i);

            BaseOptimizer.incrementIterationCount(model, 1);
        }
        return true;
    }

这一部分代码实际上涵盖了(3)和(4)两大部分的逻辑。其中，(3)中还有很多的具体的操作，比如计算残差的值等等。这里就不一一详述了，如果有需要的话，可以自行在IDE中进行调试。
最后，我这边给出经过500轮次训练过程的可视化信息图片。Web UI的地址是本地：localhost:9000/train/overview

 

左上角的第一张图是Loss Score vs Iteration。也就是说每经过一次迭代后，损失函数的值。可以明显看出，Loss是振荡下降最后直到收敛。

右上角第一张图是模型的参数信息。

下面的两张图是训练过程中梯度的相关信息。

补充说明一点：UI页面需要引入相应的依赖并且JDK版本需要1.8以上：

 

		
        	org.deeplearning4j
        	deeplearning4j-ui_${scala.binary.version}
        	${dl4j.version}
    	

在最后做下小结：我们通过构建一个含有一层隐藏层的全连接神经网络来解决XOR的问题，推导了基于随机梯度下降算法的神经网络中各个参数更新的公式，并结合Deeplearning4j的部分源码进行分析以及建模验证。需要说明的是，选择XOR问题，一方面是因为该问题的训练数据少，容易解释BP算法，同时，XOR问题也是经典的需要通过非线性特征变换才可以解决的问题。换句话说，如果将隐藏层中的Relu函数换成Identity，那么模型将不会收敛。