Pytorch：深度学习基础及数学原理

Pytorch：深度学习基础及数学原理

监督学习和无监督学习

常见机器学习方法：

• 监督学习：通过已有的训练样本（即已知数据及对应的输出）去训练得到一个最优模型，再利用这个模型将所有的输入映射为相应的输出
• 无监督学习：没有已训练样本，需要对数据进行建模
• 半监督学习：在训练阶段结合大量未标记的数据和少量的标签数据。使用训练集训练的模型在训练时更为准确
• 强化学习：设定一个回报函数，通过这个函数来确认是否与目标值越来越接近。

线性回归

线性回归是利用数理统计中回归分析，来确定两种或两种以上的变量间的相互依赖的定量关系的一种统计方法
回归分析中，只包含一个自变量和一个因变量，并且二者的关系可以用一条直线近似表示，这种回归分析称为一元线性回归分析。如包含两个或两个以上的自变量，且自变量与因变量之间是线性关系，则称为多元线性回归

import torch
from torch.nn import Linear, Module, MSELoss
from torch.optim import SGD
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# 定义一个线性函数， y = 2x + 3
x = np.linspace(0, 20, 500)
y = 3 * x + 5
plt.plot(x, y)

[]

# 生成随机的点，作为训练数据
x = np.random.rand(256)
noise = np.random.randn(256) / 4
y = 3 * x + 5 + noise
df = pd.DataFrame()
df['x'] = x
df['y'] = y

# 显示数据
sns.lmplot(x='x', y='y', data=df)

# 训练
model = Linear(1, 1)
# 参数代表输入输出的特征（features）数量都是1， Linear模型的表达式为y=w*x+b,其中w代表权重，b代表偏置
criterion = MSELoss()
# MSDLoss均方误差
optimizer = SGD(model.parameters(), lr=0.01)
# 优化器选择常见的SGD优化器，即每一次计算batch梯度，学习率0.01
epochs = 2000
# 训练2000次
# 准备训练数据，x_train,y_train的形状（256，1），代表batch大小为256， features为1， astype为float32
x_train = x.reshape(-1, 1).astype('float32')
y_train = y.reshape(-1, 1).astype('float32')

# 开始训练
for i in range(epochs):
    # 整理输入和输出符合torch的Tensor类型
    inputs = torch.from_numpy(x_train)
    labels = torch.from_numpy(y_train)
    # 使用模型预测
    outputs = model(inputs)
    # 重置权重
    optimizer.zero_grad()
    # 计算损失
    loss = criterion(outputs, labels)
    # 反向传播
    loss.backward()
    # 使用优化器默认优化方法
    optimizer.step()
    if i % 100 == 0:
        print('epoch {}, loss: {:.3f}'.format(i, loss.data.item()))

epoch 0, loss: 35.537
epoch 100, loss: 0.294
epoch 200, loss: 0.074
epoch 300, loss: 0.070
epoch 400, loss: 0.068
epoch 500, loss: 0.066
epoch 600, loss: 0.065
epoch 700, loss: 0.064
epoch 800, loss: 0.063
epoch 900, loss: 0.063
epoch 1000, loss: 0.062
epoch 1100, loss: 0.062
epoch 1200, loss: 0.062
epoch 1300, loss: 0.062
epoch 1400, loss: 0.061
epoch 1500, loss: 0.061
epoch 1600, loss: 0.061
epoch 1700, loss: 0.061
epoch 1800, loss: 0.061
epoch 1900, loss: 0.061

# 使用model.parameters提取模型参数，w和b是需要训练的模型参数
[w, b] = model.parameters()
print('w:', w.item(), 'b:', b.item())

w: 3.033578872680664 b: 4.967657089233398

# 可视化模型
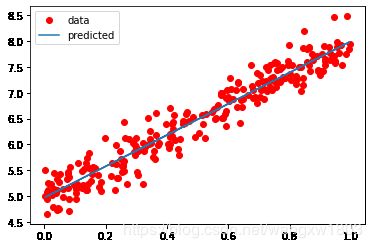
predicted = model.forward(torch.from_numpy(x_train)).data.numpy()
plt.plot(x_train, y_train, 'go', label='data', color='red')
plt.plot(x_train, predicted, label='predicted')
plt.legend()
plt.show()

损失函数（Loss Function）

损失函数是用来估量模型的预测值与真实值的差异程度，它是一个非负数，且数值越小则模型性能越好。
训练模型的过程即为通过不断迭代计算，使用梯度下降优化算法，使得损失函数越来越小，以达到模型最优

Pytorch内置损失函数

nn.L1loss(reduction='sum')

参数：reduction有三个参数，none:不适用约简，mean:返回loss的平均值，sum:返回loss的和。默认mean 输入x与目标y之间的绝对值，要求x与y的维度一样，得到的loss维度也是一样:

$loss(x,y)=1/n\Sigma |x_i-y_i|$

nn.NLLLoss(weight=None,ignore_index=-100,reduction='mean')

用于多分类的负对数似然损失函数:

$loss(x,class)=-x[class]$

NLLLoss中如果传递了weight参数，会对损失函数进行加权，公式即变成:

$loss(x,class)=-weight[class]\ast x[class]$

nn.MSELoss(reduction='mean')

均方误差损失函数，输入x和目标值y之间的均方差

$loss(x,y)=1/n\Sigma (x_i-y_i{)}^2$

nn.CrossEntropyLoss(weight=None,ignore_index=-100,reduction='mean')

参数：weight(Tensor， optional)-自定义的每个类别的权重，必须是长度为C的Tensor；ignore_index(int, optional) -设置一个目标值，该值会被忽略，从而不影响到输入的梯度；reduction同上 多分类用的交叉熵损失函数，LogSoftMax和NLLLoss集成到一个类中，会调用nn.NLLLoss函数，可以理解为：

CrossEntropyLoss() = log_softmax() + NLLLoss()

$losss(x,class)=-log\frac{exp(x[class]}{{\Sigma }_{j}exp(x[j])}$

因为使用了NLLLoss，所以可以传入weight参数，这时loss的计算公式变为：

$loss(x,y)=weights[class]\ast (-x[class]+log({\Sigma }_{j}exp(x[j])))$

所以一般多分类的情况会使用这个损失函数

nn.BCELoss

计算x与y之间的二进制交叉熵

$loss(o,t)=-\frac{1}{n}{\Sigma }_i(t[i]\ast log(o[i]+(1-t[i])\ast log(1-o[i]))$

用的时候需要在该层前面加Sigmoid函数

梯度下降

梯度下降是一个使损失函数越来越小的优化算法，在约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一。

梯度

梯度的本意是一个向量（矢量），标识某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）
我们需要最小化损失函数，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数

Mini_batch的梯度下降法

对于整个训练集进行梯度下降法的时候，我们必须处理整个训练数据集，然后才能进行梯度下降，即每一步梯度下降法需要对整个训练集进行一次处理，如果训练集很大的时候处理速度会很慢，而且也不可能一次的载入到内存或显存中，所以要把大数据集分成小数据集，一部分一部分的训练，这个训练子集即称为Mini_batch。
对于普通的梯度下降法，一个epoch只能进行一次梯度下降，而对于Mini_batch梯度下降法，一个epoch可以进行Mini_batch的个数次梯度下降

• 如果训练样本的大小比较小时，能够一次性的读取到内存中，那就不需要使用Mini_batch
• 如果训练样本的大小比较大时，一次读入不到内存或显存中，那么必须使用Mini_batch来分批的计算
• Mini_batch size的计算规则如下，在内存允许的最大情况下使用2的N次方个size

torch.optim.SGD

随机梯度下降算法，带有动量(momentum)的算法作为一个可选参数进行设置

optimizer = torch.optim.SGD(model.parameters(), lr=0.1, moment_num=0.9)

torch.optim.RMSprop

RMSprop(root mean square prop)也是一种可以加快梯度下降的算法，利用RMSprop算法，可以减小某些维度更新波动较大的情况，使其梯度下降的变化最快

optimizer = torch.optim.RMSprop(model.parameters(), lr=0.1, alpha=0.99)

torch.optim.Adam

Adam优化算法的基本思想就是将Momentnum和RMSprop结合起来的一种适用于不同深度学习结构的优化算法

optimizer = torch.optim.Adam(model.parameters(), lr=0.01, betas=(0.9, 0.99), eps=1e-08)

方差/偏差

• 偏差度量了学习算法的期望预测与真实结果的偏离程序，即算法本身的拟合能力
• 方差度量了同样大小的训练集的变动所导致的学习性能的变化，即模型的泛化能力

1. 高偏差：一般称为欠拟合（underfitting），即莫i选哪个并没有很好的适配现有数据，拟合度不够
2. 高方差：一般称为过拟合（overfitting），即模型对于训练的拟合度太高了，失去了泛化能力

解决方法

欠拟合：

1. 增加网络结构，如增加隐藏层数目
2. 训练更长的时间
3. 寻找合适的网络架构，使用更大的NN结构

过拟合：

1. 使用更多数据
2. 正则化（regularization）
3. 寻找合适的网络结构

# 计算偏差
print(3-w.data.item(), 5-b.data.item())

-0.03357887268066406 0.03234291076660156

正则化

利用正则化解决高方差问题，正则化在Cost function中加入正则化项，惩罚模型的复杂度

L1正则化

在损失函数的基础上加上权重参数的绝对值

$L=E_{i}n+\lambda {\Sigma }_j|w_j|$

L2正则化

在损失函数的基础上加权重参数的平方和

$L=E_{i}n+\lambda {\Sigma }_j{w}_j^2$

L1比L2更容易获得稀疏解

• W大于1的时候， L2正则项的w更新速度比L1快；当w小于1的时候，L1比L2快，而且L1的w更新很容易就能到0；
• L2正则项，w的分布时高斯分布（对高斯概率密度函数取log得到w的平方项）；L1正则项，w的分布是拉普拉斯分布（对Laplace概率密度函数取log得到w的绝对值项）