Python实战——ESIM 模型搭建(keras版)
文章目录
- 1. input encoding
- 1.1 原理
- 1.2 实现
- 2. local inference modeling
- 2.1 原理
- 2.2 实现
- 3. inference composition
- 3.1 原理
- 3.2 实现
ESIM 原理笔记见: 论文笔记&翻译——Enhanced LSTM for Natural Language Inference(ESIM)
ESIM主要分为三部分:input encoding,local inference modeling 和 inference composition。如上图所示,ESIM 是左边一部分, 如下图所示
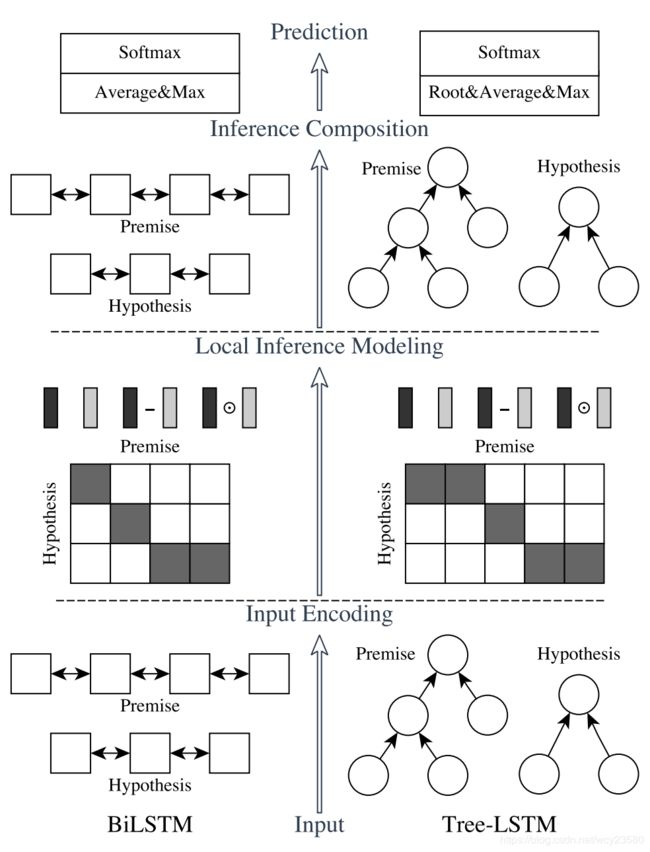
三部分简要代码如下:
1. input encoding
1.1 原理
a ˉ i = B i L S T M ( a , i ) , ∀ i ∈ [ 1 , 2 , . . . , l a ] \bar{a}_i = BiLSTM(a, i), \forall i \in [1, 2, ..., l_a] aˉi=BiLSTM(a,i),∀i∈[1,2,...,la]
b ˉ j = B i L S T M ( b , j ) , ∀ j ∈ [ 1 , 2 , . . . , l b ] \bar{b}_j = BiLSTM(b, j), \forall j \in [1, 2, ..., l_b] bˉj=BiLSTM(b,j),∀j∈[1,2,...,lb]
1.2 实现
i1 = Input(shape=(SentenceLen,), dtype='float32')
i2 = Input(shape=(SentenceLen,), dtype='float32')
x1 = Embedding([CONFIG])(i1)
x2 = Embedding([CONFIG])(i2)
x1 = Bidirectional(LSTM(300, return_sequences=True))(x1)
x2 = Bidirectional(LSTM(300, return_sequences=True))(x2)
2. local inference modeling
2.1 原理
a i ^ = ∑ j = 1 l b exp e i j ∑ k = 1 l b exp ( e i k ) b ˉ , ∀ i ∈ [ 1 , 2 , . . . , l a ] \hat{a_i} = \sum_{j=1}^{l_b} \frac{\exp{e_{ij}}}{\sum_{k=1}^{l_b} \exp(e_{ik})} \bar{b}, \forall i \in [1, 2, ..., l_a] ai^=j=1∑lb∑k=1lbexp(eik)expeijbˉ,∀i∈[1,2,...,la]
b j ^ = ∑ i = 1 l a exp e i j ∑ k = 1 l a exp ( e k j ) a ˉ , ∀ j ∈ [ 1 , 2 , . . . , l b ] \hat{b_j} = \sum_{i=1}^{l_a} \frac{\exp{e_{ij}}}{\sum_{k=1}^{l_a} \exp(e_{kj})} \bar{a}, \forall j \in [1, 2, ..., l_b] bj^=i=1∑la∑k=1laexp(ekj)expeijaˉ,∀j∈[1,2,...,lb]
2.2 实现
e = Dot(axes=2)([x1, x2])
e1 = Softmax(axis=2)(e)
e2 = Softmax(axis=1)(e)
e1 = Lambda(K.expand_dims, arguments={'axis' : 3})(e1)
e2 = Lambda(K.expand_dims, arguments={'axis' : 3})(e2)
_x1 = Lambda(K.expand_dims, arguments={'axis' : 1})(x2)
_x1 = Multiply()([e1, _x1])
_x1 = Lambda(K.sum, arguments={'axis' : 2})(_x1)
_x2 = Lambda(K.expand_dims, arguments={'axis' : 2})(x1)
_x2 = Multiply()([e2, _x2])
_x2 = Lambda(K.sum, arguments={'axis' : 1})(_x2)
3. inference composition
3.1 原理
m a = [ a ˉ ; a ^ ; a ˉ − a ^ ; a ˉ ⊙ a ^ ] m_a = [\bar{a}; \hat{a}; \bar{a} - \hat{a}; \bar{a} \odot \hat{a}] ma=[aˉ;a^;aˉ−a^;aˉ⊙a^]
m b = [ b ˉ ; b ^ ; b ˉ − b ^ ; b ˉ ⊙ b ^ ] m_b = [\bar{b}; \hat{b}; \bar{b} - \hat{b}; \bar{b} \odot \hat{b}] mb=[bˉ;b^;bˉ−b^;bˉ⊙b^]
v a , i = B i L S T M ( m a , i ) v_{a,i} = BiLSTM(m_a, i) va,i=BiLSTM(ma,i)
v b , j = B i L S T M ( m b , j ) v_{b,j} = BiLSTM(m_b, j) vb,j=BiLSTM(mb,j)
v a , a v e = ∑ i = 1 l a v a , i l a v_{a,ave} = \sum_{i=1}^{l_a} \frac{v_{a,i}}{l_a} va,ave=i=1∑lalava,i
v a , m a x = max i = 1 l a v a , i v_{a,max} = \max_{i=1}^{l_a} v_{a,i} va,max=i=1maxlava,i
v b , a v e = ∑ j = 1 l b v b , j l b v_{b,ave} = \sum_{j=1}^{l_b} \frac{v_{b,j}}{l_b} vb,ave=j=1∑lblbvb,j
v b , m a x = max j = 1 l b v b , j v_{b,max} = \max_{j=1}^{l_b} v_{b,j} vb,max=j=1maxlbvb,j
v = [ v a , a v e ; v a , m a x ; v b , a v e ; v b , m a x ] v = [v_{a,ave}; v_{a,max}; v_{b,ave}; v_{b,max} ] v=[va,ave;va,max;vb,ave;vb,max]
3.2 实现
m1 = Concatenate()([x1, _x1, Subtract()([x1, _x1]), Multiply()([x1, _x1])])
m2 = Concatenate()([x2, _x2, Subtract()([x2, _x2]), Multiply()([x2, _x2])])
y1 = Bidirectional(LSTM(300, return_sequences=True))(m1)
y2 = Bidirectional(LSTM(300, return_sequences=True))(m2)
mx1 = Lambda(K.max, arguments={'axis' : 1})(y1)
av1 = Lambda(K.mean, arguments={'axis' : 1})(y1)
mx2 = Lambda(K.max, arguments={'axis' : 1})(y2)
av2 = Lambda(K.mean, arguments={'axis' : 1})(y2)
y = Concatenate()([av1, mx1, av2, mx2])
y = Dense(1024, activation='tanh')(y)
y = Dropout(0.5)(y)
y = Dense(1024, activation='tanh')(y)
y = Dropout(0.5)(y)
y = Dense(2, activation='softmax')(y)