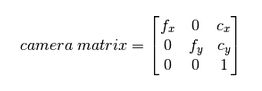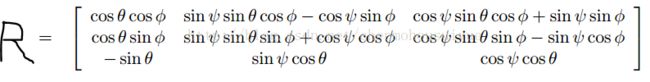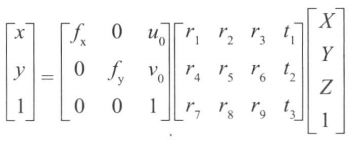单目相机标定——相机外参估计（二）

前言

在上一篇用python调用Opencv做了相机内参求取，当时也没有做任何思考，就是一味的找demo，然后试着自己敲代码。这几天认真的学了一下，发现了一些这前没考虑的东西，于是赶快记录下来。

我们为什么需要相机标定？相机标定了什么？

首先，回答第一个问题，因为相机生产过程的工艺，相机成像传感器一定不是完美的，所以通过相机看到的view和人眼看到的是不一样，也就是图像有畸变；另外，相机安装的位置使得镜头所在平面与被成像平面不是水平的，而是有夹角的，所以通过相机看到的物体的位置与物体实际的位置像是不匹配的。于是相机在使用（尤其是用作测距、定位等）之前进行标定是必要的。

第二个问题，相机标定了什么。标定相机的内参数和外参数。

内参数主要是相机的基础矩阵和畸变向量。

外参数主要是相机的旋转矩阵

和平移向量T=[t1,t2,t3]'。

我们都知道下面的公式：

(x,y)是图像平面的物理坐标，(X,Y,Z)为实际的世界坐标。它们的关系就是x=M*[R][T]*X，所以相机标定的内外参数是关乎物体实际坐标到相机图像的物理坐标的转换。

我们在相机标定（视觉定位）要考虑的问题：

1.世界坐标←→相机坐标

就是将物体在世界中的坐标对应到相机坐标中，在这个过程中需要相机的外参：旋转矩阵R和平移向量T。

2.相机坐标←→图像的物理坐标

在这个过程中，是一个光学投影的过程，需要使用到相机的内参：焦距f、焦点坐标(u0,v0)等，也就是相机的基本矩阵。

3.图像的物理坐标←→图像的像素坐标

这个过程就是在步骤2的基础上，将物理坐标中的单位距离mm转换为像素pixel个数。

4.真实图像←→理想图像

理想很美好，现实很残酷，真正得到的图像是有畸变的，所以这里将用到畸变向量去矫正图像。

解决以上四个变换，我们就可以将世界坐标中的点和图像中的像素随意转换了。

在上一篇，我们求取了相机的内部参数，同时对于固定的一个模型（相机位置、视角固定，相机看到的平面确定），角点的世界坐标和对应的像素坐标我们已知，根据这些参数我们使用opencv中的solvePnPRansac()可以很容易求得相机的外部参数。

完整代码如下：

import cv2
import numpy as np

#读取相机内参
with np.load('C:\\Users\\wlx\\Documents\\py_study\\camera calibration\\data\\intrinsic_parameters.npz') as X:
    mtx,dist = [X[i] for i in ('mtx','dist')]

def draw(img, corners, imgpts):
    corner = tuple(corners[0].ravel())
    img = cv2.line(img, corner, tuple(imgpts[0].ravel()), (255,0,0), 5)
    img = cv2.line(img, corner, tuple(imgpts[1].ravel()), (0,255,0), 5)
    img = cv2.line(img, corner, tuple(imgpts[2].ravel()), (0,0,255), 5)
    return img

#标定图像保存路径
photo_path = "C:\\Users\\wlx\\Documents\\py_study\\camera calibration\\image\\6.jpg"
#标定图像
def calibration_photo(photo_path):
    #设置要标定的角点个数
    x_nums = 8                                                          #x方向上的角点个数
    y_nums = 5
    #设置(生成)标定图在世界坐标中的坐标
    world_point = np.zeros((x_nums * y_nums,3),np.float32)            #生成x_nums*y_nums个坐标，每个坐标包含x,y,z三个元素
    world_point[:,:2] = np.mgrid[:x_nums,:y_nums].T.reshape(-1, 2)    #mgrid[]生成包含两个二维矩阵的矩阵，每个矩阵都有x_nums列,y_nums行
                                                                        #.T矩阵的转置
                                                                        #reshape()重新规划矩阵，但不改变矩阵元素
    #设置世界坐标的坐标
    axis = np.float32([[3,0,0], [0,3,0], [0,0,-3]]).reshape(-1,3)
    #设置角点查找限制
    criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER,30,0.001)

    image = cv2.imread(photo_path)

    gray = cv2.cvtColor(image,cv2.COLOR_RGB2GRAY)
    #查找角点
    ok,corners = cv2.findChessboardCorners(gray,(x_nums,y_nums),)
    #print(ok)
    if ok:
        #获取更精确的角点位置
        exact_corners = cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)

        #获取外参
        _,rvec, tvec, inliers = cv2.solvePnPRansac(world_point, exact_corners, mtx, dist)

        imgpts, jac = cv2.projectPoints(axis, rvec, tvec, mtx, dist)
        #可视化角点
        img = draw(image, corners, imgpts)
        cv2.imshow('img', img)



if __name__ == '__main__':
    calibration_photo(photo_path)
    cv2.waitKey()
    cv2.destroyAllWindows()

实现的思路：

首先，读入一张坐标图纸（也可以是你在任意一个平面做的世界坐标，因为在现实中坐标也是认为定义的），这里读取的是一张用来标定的图，然后为40个角点定义坐标，每个角点的Z坐标等于0；

然后，通过opencv的角点检测函数，找到图像中40个角点，并可以获取对应图像的像素坐标；

接着，使用_,rvec, tvec, inliers = cv2.solvePnPRansac(world_point, exact_corners, mtx, dist)获得旋转矩阵和平移向量。

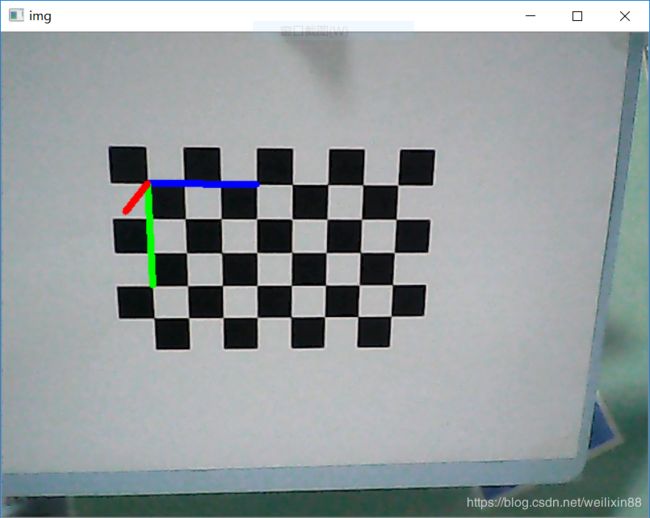
最后，将自己定义的三个世界坐标，又通过相机的内参和外参，将其转换为了像素坐标；把这些像素坐标和第一个角点的像素坐标连线，就画出了二维图像中的三维坐标轴。

问题1：相机标定内参的时候通过calibrateCamera()函数能够获得旋转矢量rvec和平移向量tvec；在本章中，我们使用solvePnPRansac()函数又一次获得旋转矢量rvec和平移向量tvec。这是为什么呢？

calibrateCamera()函数求取的旋转矢量rvec和平移向量tvec，是在获取了相机内参mtx, dist之后，通过内部调用solvePnPRansac()函数获得的。也就是说，如果对于只有一张标定图像的情况，alibrateCamera()函数求取的旋转矢量rvec和平移向量tvec，与solvePnPRansac()函数求取的旋转矢量rvec和平移向量tvec是一样的（这是确定的）。但是我们在标定相机内参的时候，为了得到较为准确的标定结果，所以拍摄了多张（10~20）不同角度的标定图，在这些标定图一起作用下，求出了相机的内参。所以当在一个确定的场景下，想要获得相机的外参时，我们需要重新求取旋转矩阵和平移向量，于是我们用了solvePnPRansac()函数（为什么不用calibrateCamera()函数了？因为calibrateCamera()函数就是调用的solvePnPRansac()函数）。

问题2:得出的rvec怎么是3*1的矩阵？

调用solvePnPRansac()函数得到的rvec是一个旋转矢量，需要使用cv2.Rodrigues(src,dst,jacobian=None)

src:输入的矩阵可以是（3*1或1*3）也可以是3*3

dst:输出的矩阵，对应输入3*3,或者（3*1或1*3）

jacobian:也是一个输出，该输出表明了输入矩阵和输出矩阵的的雅可比

转换后的矩阵就和前面的旋转矩阵对应了，然后就能求出相机的俯仰角、偏航角、滚轮角。（不过对于实际应用中，知道旋转矩阵不就行了？）

OK，相机内外参数都弄明白了，相机标定告一段落。

Goodnight