自编码器

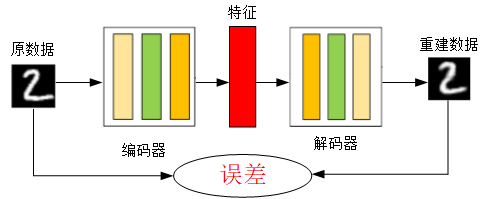
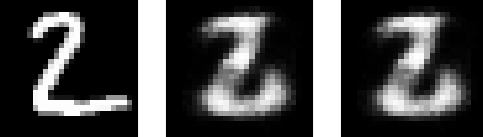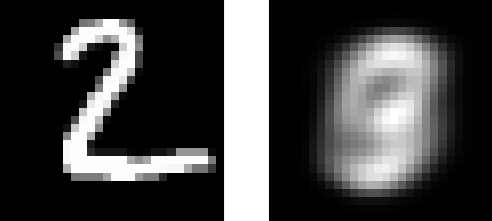　　神经网络就是最简单的自动编码器，区别在于其输出和输入是相同的，然后训练器参数，得到每一层中的权重，自然地我们就得到了输入x的不同的表示_{（每一层代表一种）}这些就是特征，自动编码器就是一种尽可能复现原数据的神经网络。

　　“自编码”是一种数据压缩算法，其中压缩和解压缩过程是有损的。自编码训练过程，不是无监督学习而是自监督学习。

　　自编码器（AutoEncoder,AE）是一种利用反向传播算法取得使输入值和输出值误差最小的特征。自动编码器由两部分组成：

1. 编码器Encoder：将输入值进行特征提取，数据降维
2. 解码器Decoder：将特征还原为原始数据

我们应该已经发现，相比于原数据重建数据变得模糊了，自编码器是一个有损无监督的过程，但是自编码器的目的不是求得损失函数最小的重建数据，而是使得误差最小的特征，，自编码器的目的：

1. 特征提取
2. 数据降维
3. 数据去噪

　　自编码器和PCA（主成分分析）有点相似，但是效果超越了PCA。

　　自动编码器只能压缩那些与训练数据类似的数据。训练好的自编码器只适用于一种编码的数据集。如果另外一种数据集采用了不同的编码，则这个自编码器不能起到很好的压缩效果。训练自编码器，可以使输入通过编码器和解码器后，保留尽可能多的信息，但也可以训练自编码器来使新表征具有多种不同的属性。不同类型的自编码器旨在实现不同类型的属性。下面将重点介绍四种不同的自编码器。

 

基本自编码器

　　香草自编码器，只有三层网络，即只有一个隐藏层的神经网络。它的输入和输出是相同的，可通过使用Adam优化器和均方误差损失函数，来学习如何重构输入。

　　隐藏层的压缩维度为32，小于输入维度784，因此这个编码器是有损的，通过这个约束，来迫使神经网络来学习数据的压缩表征。

from keras.layers import Input, Dense
from keras.models import Model
import numpy as np
import matplotlib.pyplot as plt

# 读取数据
path = './mnist.npz'
f = np.load(path)
x_train, y_train = f['x_train'], f['y_train']   # (60000, 28, 28), (60000,)
x_test, y_test = f['x_test'], f['y_test']       # (60000, 28, 28), (10000,)
f.close()

x_train = x_train.astype('float32') / 255.      # 归一化
x_test = x_test.astype('float32') / 255.        # 归一化
x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))   # (60000, 784)
x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))       # (60000, 784)

encoding_dim = 32   # 压缩维度
input_img = Input(shape=(784,))

encoded = Dense(encoding_dim, activation='relu')(input_img)        # 编码层 (?, 32)
decoded = Dense(784, activation='sigmoid')(encoded)                # 解码层 (?, 784)

autoencoder = Model(inputs=input_img, outputs=decoded)            # 自编码器模型
encoder = Model(inputs=input_img, outputs=encoded)                # 编码器模型

decoder_input = Input(shape=(encoding_dim,))
decoder_layer = autoencoder.layers[-1]

decoder = Model(inputs=decoder_input, outputs=decoder_layer(decoder_input))

autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')
# 自编码器的输入和输出都是自己
autoencoder.fit(x_train, x_train, epochs=10, batch_size=256, shuffle=True, validation_data=(x_test, x_test))

encoded_imgs = encoder.predict(x_test)
decoded_imgs = decoder.predict(encoded_imgs)
autoencoder_imgs = autoencoder.predict(x_test)


plt.subplot(1, 3, 1)
plt.imshow(x_test[1].reshape(28, 28))       # 原数据
plt.gray()  # 灰度图
ax.get_xaxis().set_visible(False)   # 除去 x 刻度
ax.get_yaxis().set_visible(False)   # 除去 y 刻度

plt.subplot(1, 3, 2)
# 编码后的数据可能已经不是图片数据了，所以这里展示解码数据
plt.imshow(decoded_imgs[1].reshape(28, 28))
plt.gray()  # 灰度图
ax.get_xaxis().set_visible(False)   # 除去 x 刻度
ax.get_yaxis().set_visible(False)   # 除去 y 刻度

ax = plt.subplot(1, 3, 3)
plt.imshow(autoencoder_imgs[1].reshape(28, 28)) # 自编码器后的数据其实和解码后的数据一样
plt.gray()  # 灰度图
ax.get_xaxis().set_visible(False)   # 除去 x 刻度
ax.get_yaxis().set_visible(False)   # 除去 y 刻度

plt.show()

图像1是原图，图像2是解码器的图，图像3是自动编码器的图

多层自编码器

　　这里搭建了一个8层隐藏层的自编码器，编码器4层，解码器4层

import numpy as np  from keras.datasets import mnist  
from keras.models import Model 　　# 泛型模型  
from keras.layers import Dense, Input  
import matplotlib.pyplot as plt  

# 读取数据
path = './mnist.npz'
f = np.load(path)
x_train, y_train = f['x_train'], f['y_train']
x_test, y_test = f['x_test'], f['y_test']
f.close()
  
# 数据预处理  
x_train = x_train.astype('float32') / 255.        # 归一化
x_test = x_test.astype('float32') / 255.        # 归一化 
x_train = x_train.reshape((x_train.shape[0], -1))   # (60000 28*28)
x_test = x_test.reshape((x_test.shape[0], -1))  # (10000, 28*28)

encoding_dim = 2          # 压缩特征维度至2维
input_img = Input(shape=(784,))          # 输入占位符
  
# 编码层  
encoded = Dense(128, activation='relu')(input_img)  
encoded = Dense(64, activation='relu')(encoded)  
encoded = Dense(10, activation='relu')(encoded)  
encoder_output = Dense(encoding_dim)(encoded)  
  
# 解码层  
decoded = Dense(10, activation='relu')(encoder_output)  
decoded = Dense(64, activation='relu')(decoded)  
decoded = Dense(128, activation='relu')(decoded)  
decoded = Dense(784, activation='tanh')(decoded)  

encoder = Model(inputs=input_img, outputs=encoder_output)   # 搭建编码模型 
autoencoder = Model(inputs=input_img, outputs=decoded)  # 搭建自编码模型  

autoencoder.compile(optimizer='adam', loss='mse')   # 编译自动编码器
# 编码器的输出和输入都是自己
autoencoder.fit(x_train, x_train, epochs=10, batch_size=256, shuffle=True)  
 
# plotting  
encoded_imgs = encoder.predict(x_test)  
decoded_imgs = autoencoder.predict(x_test)
 
# 原图
ax = plt.subplot(1, 2, 1)
plt.imshow(x_test[1].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)

# 自动编码器的图
ax = plt.subplot(1, 2, 2)
plt.imshow(decoded_imgs[1].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

图像1是原图，图像2是压缩解码后的图

卷积自编码器：用卷积层构建自编码器

　　当输入是图像时，使用卷积神经网络是更好的。卷积自编码器的编码器部分由卷积层和MaxPooling层构成，MaxPooling负责空域下采样。而解码器由卷积层和上采样层构成。

keras.layers.MaxPooling2D((2, 2), padding='same')   # 负责下采样 
keras.layers.convolutional.UpSampling2D((2, 2))  # 负责上采样

 

from keras.layers import Input, Convolution2D, MaxPooling2D, UpSampling2D  
from keras.models import Model  
import numpy as np  
import matplotlib.pyplot as plt  
from keras.callbacks import TensorBoard  
 
# 读取数据
path = './mnist.npz'
f = np.load(path)
x_train, y_train = f['x_train'], f['y_train']
x_test, y_test = f['x_test'], f['y_test']
f.close()
  
# 数据预处理  
x_train = x_train.astype('float32') / 255.        # minmax_normalized  
x_test = x_test.astype('float32') / 255.          # minmax_normalized  
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1))      # shape (60000, 28, 28, 1)
x_test = np.reshape(x_test, (len(x_test), 28, 28, 1))          # shape (10000, 28, 28, 1)        

input_img = Input(shape=(28, 28, 1))  

# 编码器
x = Convolution2D(16, (3, 3), activation='relu', padding='same')(input_img)  
print(x.shape)        # (?, 28, 28, 16)
x = MaxPooling2D((2, 2), padding='same')(x)  
print(x.shape)        # (?, 14, 14, 16)
x = Convolution2D(8, (3, 3), activation='relu', padding='same')(x)  
print(x.shape)        # (?, 14, 14, 8)
x = MaxPooling2D((2, 2), padding='same')(x)  
print(x.shape)        # (?, 7, 7, 8)
x = Convolution2D(8, (3, 3), activation='relu', padding='same')(x)  
print(x.shape)        # (?, 7, 7, 8)
encoded = MaxPooling2D((2, 2), padding='same')(x)  
print(encoded.shape)        # (?, 4, 4, 8)

# 解码器
x = Convolution2D(8, (3, 3), activation='relu', padding='same')(encoded)  
print(x.shape)        # (?, 4, 4, 8)
x = UpSampling2D((2, 2))(x)  
print(x.shape)        # (?, 8, 8, 8)
x = Convolution2D(8, (3, 3), activation='relu', padding='same')(x)  
print(x.shape)        # (?, 8, 8, 8)
x = UpSampling2D((2, 2))(x)  
print(x.shape)        # (?, 16, 16, 8)
x = Convolution2D(16, (3, 3), activation='relu')(x)  
print(x.shape)        # (?, 14, 14, 16)
x = UpSampling2D((2, 2))(x)  
print(x.shape)        # (?, 28, 28, 16)
decoded = Convolution2D(1, (3, 3), activation='sigmoid', padding='same')(x)  
print(decoded.shape)        # (?, 28, 28, 1)
  
autoencoder = Model(inputs=input_img, outputs=decoded)  
autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')  

# 自编码器的输入和输出都是自己
autoencoder.fit(x_train, x_train, epochs=10, batch_size=256,  
                shuffle=True, validation_data=(x_test, x_test),  
                callbacks=[TensorBoard(log_dir='autoencoder')])  
  
decoded_imgs = autoencoder.predict(x_test)  

# 原图
ax = plt.subplot(1, 2, 1)
plt.imshow(x_test[1].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)

# 自动编码器的图
ax = plt.subplot(1, 2, 2)
plt.imshow(decoded_imgs[1].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

　　注意：卷积后的形状，只与步幅有关，最后一个维度=卷积核的个数；当padding是“same”是填充0，“valid”时舍去多余项。

正则自编码器

　　除了添加一个比输入数据维度小的隐藏层。还可以使用一些方法用来约束自编码器重构，如正则自编码器。

　　正则自编码器不需要使用浅层的编码器和解码器以及小的编码维数来限制模型容量，而是使用损失函数来鼓励模型学习其他特性（除了将输入复制到输出）。这些特性包括稀疏表征、小导数表征、以及对噪声或输入缺失的鲁棒性。

在实际应用中，常用到两种正则自编码器，分别是稀疏自编码器和降噪自编码器。

稀疏自编码器

　　一般用来学习特征，以便用于像分类这样的任务。稀疏正则化的自编码器必须反映训练数据集的独特统计特征，而不是简单地充当恒等函数。以这种方式训练，执行附带稀疏惩罚的复现任务可以得到能学习有用特征的模型。

　　还有一种用来约束自动编码器重构的方法，是对其损失函数施加约束。比如，可对损失函数添加一个正则化约束，这样能使自编码器学习到数据的稀疏表征。

　　要注意，在隐含层中，我们还加入了L1正则化，作为优化阶段中损失函数的惩罚项。与基本自编码器相比，这样操作后的数据表征更为稀疏。

# ------- 稀疏自编码器 ------- #
x = Input(shape=(784,))
# 仅仅是比Vanilla 自编码器多一个正则项
h = Dense(32, activation='relu', activity_regularizer=regularizers.l1(10e-5))(x)   # 编码器
r = Dense(784, activation='sigmoid')(h)     # 解码器

autoencoder = Model(inputs=x, outputs=r)
autoencoder.compile(optimizer='adam', loss='mse')

history = autoencoder.fit(X_train, X_train, batch_size=128, epochs=15, verbose=1, validation_data=(X_test, X_test))
decoded_imgs = autoencoder.predict(X_test)

降噪自编码器

　　这里是通过改变损失函数的重构误差项来学习一些有用信息。

　　向训练数据加入噪声，并使自编码器学会去除这种噪声来获得没有被噪声污染过的真实输入。因此，这就迫使编码器学习提取最重要的特征并学习输入数据中更加鲁棒的表征，这也是它的泛化能力比一般编码器强的原因。

# -*- encoding:utf-8 -*-
import keras
import numpy as np
import matplotlib.pyplot as plt
from keras.models import Model
from keras.layers import Input
from keras.layers.convolutional import Conv2D, MaxPooling2D, UpSampling2D

f = np.load('./mnist.npz')
X_train, _ = f['x_train'], f['y_train']
X_test, _ = f['x_test'], f['y_test']
f.close()

X_train = X_train.astype("float32") / 255.  # 归一化
X_test = X_test.astype("float32") / 255.  # 归一化
X_train = X_train.reshape(X_train.shape[0], 28, 28, 1)  # (60000, 28, 28, 1)
X_test = X_test.reshape(X_test.shape[0], 28, 28, 1)  # (10000, 28, 28, 1)

# 创建噪声数据
noise_factor = 0.5  # 噪声因子
X_train_noisy = X_train + noise_factor * np.random.normal(0.0, 1.0, X_train.shape)
X_test_noisy = X_test + noise_factor * np.random.normal(0.0, 1.0, X_test.shape)

X_train_noisy = np.clip(X_train_noisy, 0., 1.)
X_test_noisy = np.clip(X_test_noisy, 0., 1.)

# ------- 降噪自编码器 ------- #
input_img = Input(shape=(28, 28, 1))

# 编码器
x = Conv2D(32, (3, 3), activation='relu', padding='same')(input_img)  # (?, 28, 28, 32)
x = MaxPooling2D((2, 2), padding='same')(x)  # (?, 14, 14, 32)
x = Conv2D(32, (3, 3), activation='relu', padding='same')(x)  # (?, 14, 14, 32)
encoded = MaxPooling2D((2, 2), padding='same')(x)  # (?, 7, 7, 32)
print(encoded.shape)

# 解码器
x = Conv2D(32, (3, 3), activation='relu', padding='same')(encoded)  # (?, 7, 7, 32)
x = UpSampling2D((2, 2))(x)  # (?, 14, 14, 32)
x = Conv2D(32, (3, 3), activation='relu', padding='same')(x)  # (?, 14, 14, 32)
x = UpSampling2D((2, 2))(x)  # (?, 28, 28, 32)
decoded = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(x)  # (?, 28, 28, 1)

autoencoder = Model(inputs=input_img, outputs=decoded)
autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')

# 输入是噪声数据，输出是纯净数据
history = autoencoder.fit(X_train_noisy, X_train, batch_size=128, epochs=3,
                          verbose=1, validation_data=(X_test_noisy, X_test))
decoded_imgs = autoencoder.predict(X_test_noisy)

# 原图
ax = plt.subplot(1, 2, 1)
plt.imshow(X_test[1].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)

# 自编码器的图
ax = plt.subplot(1, 2, 2)
plt.imshow(decoded_imgs[1].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

 

左边是噪声数据，右边是自编码器降噪后的数据

Sequence-to-sequence自动编码器

　　如果输入是序列而不是2D的图像，那么就要针对序列模型构造自编码器，如LSTM。要构造基于LSTM的自编码器，首先我们需要一个LSTM的编码器来将输入序列变为一个向量，然后将这个向量重复N次，然后用LSTM的解码器将这个N步的时间序列变为目标序列。

from keras.layers import Input, LSTM, RepeatVector
from keras.models import Model

inputs = Input(shape=(timesteps, input_dim))
encoded = LSTM(latent_dim)(inputs)

decoded = RepeatVector(timesteps)(encoded)
decoded = LSTM(input, return_sequences=True)(decoded)

sequence_autoencoder = Model(inputs, decoded)
encoder = Model(inputs, encoded)

变分自编码器(Variational autoencoder, VAE)：编码数据分布

　　编码自编码器是更现代和有趣的一种自动编码器，它为码字施加约束，使得编码器学习到输入数据的隐变量模型。隐变量模型是连接显变量集和隐变量集的统计模型，隐变量模型的假设是显变量是由隐变量的状态控制的，各个显变量之间条件独立。也就是说，变分编码器不再学习一个任意的函数，而是学习你的数据概率分布的一组参数。通过在这个概率分布中采样，你可以生成新的输入数据，即变分编码器是一个生成模型。

　　下面是变分编码器的工作原理：

　　首先，编码器网络将输入样本x转换为隐空间的两个参数，记作z_mean和z_log_sigma。然后，我们随机从隐藏的正态分布中采样得到数据点z，这个隐藏分布我们假设就是产生输入数据的那个分布。z = z_mean + exp(z_log_sigma)*epsilon，epsilon是一个服从正态分布的张量。最后，使用解码器网络将隐空间映射到显空间，即将z转换回原来的输入数据空间。

　　参数藉由两个损失函数来训练，一个是重构损失函数，该函数要求解码出来的样本与输入的样本相似（与之前的自编码器相同），第二项损失函数是学习到的隐分布与先验分布的KL距离，作为一个正则。实际上把后面这项损失函数去掉也可以，尽管它对学习符合要求的隐空间和防止过拟合有帮助。

　　因为VAE是一个很复杂的例子，我们把VAE的代码放在了github上，在这里。在这里我们来一步步回顾一下这个模型是如何搭建的

首先，建立编码网络，将输入影射为隐分布的参数：

x = Input(batch_shape=(batch_size, original_dim))
h = Dense(intermediate_dim, activation='relu')(x)
z_mean = Dense(latent_dim)(h)
z_log_sigma = Dense(latent_dim)(h)

然后从这些参数确定的分布中采样，这个样本相当于之前的隐层值

def sampling(args):
    z_mean, z_log_sigma = args
    epsilon = K.random_normal(shape=(batch_size, latent_dim),
                              mean=0., std=epsilon_std)
    return z_mean + K.exp(z_log_sigma) * epsilon

# note that "output_shape" isn't necessary with the TensorFlow backend
# so you could write `Lambda(sampling)([z_mean, z_log_sigma])`
z = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_sigma])

最后，将采样得到的点映射回去重构原输入：

decoder_h = Dense(intermediate_dim, activation='relu')
decoder_mean = Dense(original_dim, activation='sigmoid')
h_decoded = decoder_h(z)
x_decoded_mean = decoder_mean(h_decoded)

到目前为止我们做的工作需要实例化三个模型：

• 一个端到端的自动编码器，用于完成输入信号的重构

• 一个用于将输入空间映射为隐空间的编码器

• 一个利用隐空间的分布产生的样本点生成对应的重构样本的生成器

# end-to-end autoencoder
vae = Model(x, x_decoded_mean)

# encoder, from inputs to latent space
encoder = Model(x, z_mean)

# generator, from latent space to reconstructed inputs
decoder_input = Input(shape=(latent_dim,))
_h_decoded = decoder_h(decoder_input)
_x_decoded_mean = decoder_mean(_h_decoded)
generator = Model(decoder_input, _x_decoded_mean)

我们使用端到端的模型训练，损失函数是一项重构误差，和一项KL距离

def vae_loss(x, x_decoded_mean):
    xent_loss = objectives.binary_crossentropy(x, x_decoded_mean)
    kl_loss = - 0.5 * K.mean(1 + z_log_sigma - K.square(z_mean) - K.exp(z_log_sigma), axis=-1)
    return xent_loss + kl_loss

vae.compile(optimizer='rmsprop', loss=vae_loss)

现在使用MNIST库来训练变分编码器：

(x_train, y_train), (x_test, y_test) = mnist.load_data()

x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))

vae.fit(x_train, x_train,
        shuffle=True,
        nb_epoch=nb_epoch,
        batch_size=batch_size,
        validation_data=(x_test, x_test))

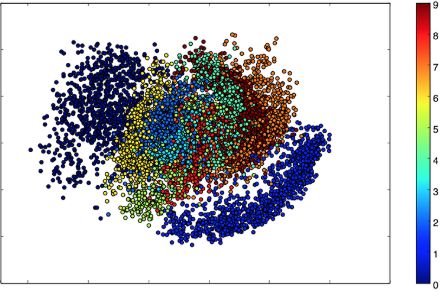
因为我们的隐空间只有两维，所以我们可以可视化一下。我们来看看2D平面中不同类的近邻分布：

x_test_encoded = encoder.predict(x_test, batch_size=batch_size)
plt.figure(figsize=(6, 6))
plt.scatter(x_test_encoded[:, 0], x_test_encoded[:, 1], c=y_test)
plt.colorbar()
plt.show()

上图每种颜色代表一个数字，相近聚类的数字代表他们在结构上相似。

因为变分编码器是一个生成模型，我们可以用它来生成新数字。我们可以从隐平面上采样一些点，然后生成对应的显变量，即MNIST的数字：

# display a 2D manifold of the digits
n = 15  # figure with 15x15 digits
digit_size = 28
figure = np.zeros((digit_size * n, digit_size * n))
# we will sample n points within [-15, 15] standard deviations
grid_x = np.linspace(-15, 15, n)
grid_y = np.linspace(-15, 15, n)

for i, yi in enumerate(grid_x):
    for j, xi in enumerate(grid_y):
        z_sample = np.array([[xi, yi]]) * epsilon_std
        x_decoded = generator.predict(z_sample)
        digit = x_decoded[0].reshape(digit_size, digit_size)
        figure[i * digit_size: (i + 1) * digit_size,
               j * digit_size: (j + 1) * digit_size] = digit

plt.figure(figsize=(10, 10))
plt.imshow(figure)
plt.show()

声码器

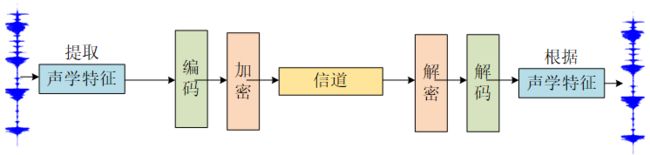
　　声码器是在传输中利用模型参数，对语音信号进行分析和合成的编、译码器。

　　声码器在发送端对语音信号进行分析，提取出语音信号的特征参量加以编码和加密，以取得和信道的匹配，经信息通道传递到接受端，再根据收到的特征参量恢复原始语音波形。

声码器的功能：

• 频域：频谱分析、鉴别清浊音、测定浊音基频谱
• 时域：利用其周期性提取一些参数进行线性预测

根据工作原理，声码器可以分为：

• 通道式声码器
• 共振峰声码器
• 图案声码器
• 线性预测声码器
• 相关声码器
• 正交函数声码器

用途：数字电话通信、特别是保密通信。

声音产生原理

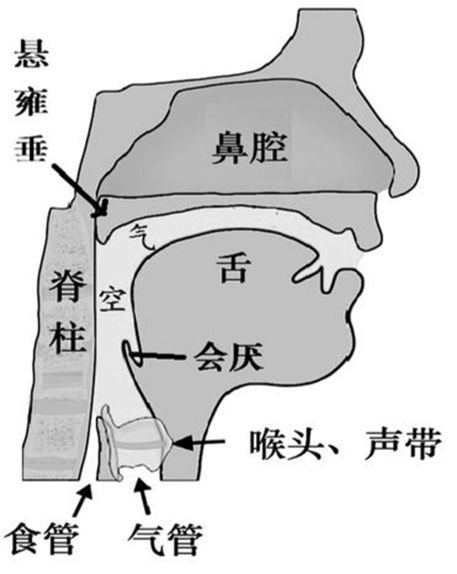
声音产生的原理：

1. 肺部产生的气流，经过喉咙形成声源激励
2. 激励经过由口腔和鼻腔构成的声道产生语音信号。

声码器在发送端首先提取主要话音参数：

1. 声源特性，如声带“振动-不振动”（浊-清 音）、声带振动时的基本频率（基频）
2. 声道传输声源信号的特性。

 

　　声音的参数变化很慢，他们占用的总频带比整个语音本身频带窄的多，因而对这些参数采样编码时总数码率只有几千甚至几百比特/秒，只有话音信号采样编码的数码率的十几分之一，因此普通的电话信道可以通过传输声音的参数，在接收端利用合成器将这些参数还原为原来的语音信号。

　　声码器被用来研究压缩语音频带。

　　压缩频带声码器能压缩频带的根本依据是：话音信号中存在信息冗余度。话音信号只要保留声源和声道的主要参量，就能保证有较高的话音清晰度。
话音参数和提取这些参数的方式不同，决定声码器的不同类型和功能。

例如：

• 共振峰声码器：用共振峰的位置、幅度和宽度表示频谱包络的
• 同态声码器：利用同态滤波技术,如对话音信号进行积分变换、取对数和反变换以获得各参数的
• 声激励声码器：直接编码和传输话音的基带（如取200～600赫的频带）以表征声源特性。

声码器模型
输入：一个快变化的激励信号语音信号
输出：一个慢变化的声道滤波器后所得的输出

语音信号可以用两组参数表示。

• 激励源（清浊音指示、基音频率和幅度）的参数
• 代表声道滤波器的响应的参数

这些参数，特别是代表声道滤波器响应的参数所取的不同的具体形式就构成了各种不同的声码器。

　　由于声码器只传递模型参数，完全去除了语音模型所揭示的语音信号中的多余性，因而可得到巨大的压缩效果

　　波形编码器虽然也可利用语音模型对语音进行压缩，但不管怎样它总还需要传送按语音模型无法预测的那部分信号波形或信号频谱。这些按模型预测后的误差信号代表了我们尚未了解的、在模型中尚未得到反映的语音细节。

　　大部分声码器都利用了人耳对相位不敏感这一特性，在进行语音分析和合成时只对语音信号的幅度谱有所要求。所以合成语音与原始语音在波形上很难加以比较。

优点是数码率低，因而适合于窄带、昂贵和劣质信道条件下的数字电话通信，能满足节约频带、节省功率和抗干扰编码的要求。
有利于对语音的存储和语音的加密处理。

缺点是音质不如普通数字电话好，而且工作过程较复杂，造价较高，音质有点差。 现代声码器主要用于军队、政府以及那些值得付出代价以换取通信安全（保密）的场合。

 

参考文献

Keras 自编码器AutoEncoder

百度百科--声码器

自动编码器：各种各样的自动编码器 Keras官方网站写的非常好！

 

转载于:https://www.cnblogs.com/LXP-Never/p/10921257.html