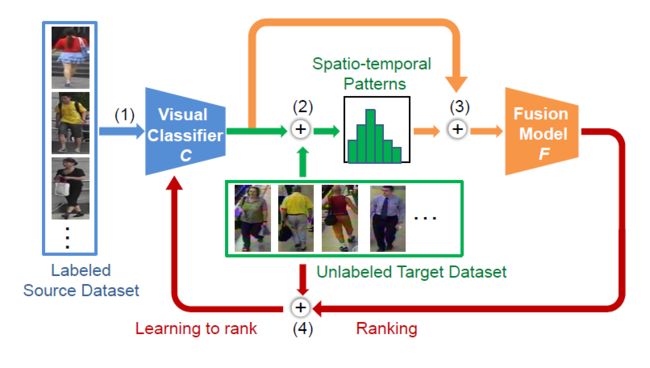
论文可以在arxiv下载,老板一作,本人二作,也是我们实验室第一篇CCF A类论文,这个方法我们称为TFusion。
代码:https://github.com/ahangchen/TFusion
- 解决的目标是跨数据集的Person Reid
- 属于无监督学习
- 方法是多模态数据融合 + 迁移学习
- 实验效果上,超越了所有无监督Person reid方法,逼近有监督方法,在部分数据集上甚至超越有监督方法
本文为你解读CVPR2018 TFusion
转载请注明作者梦里茶
Task
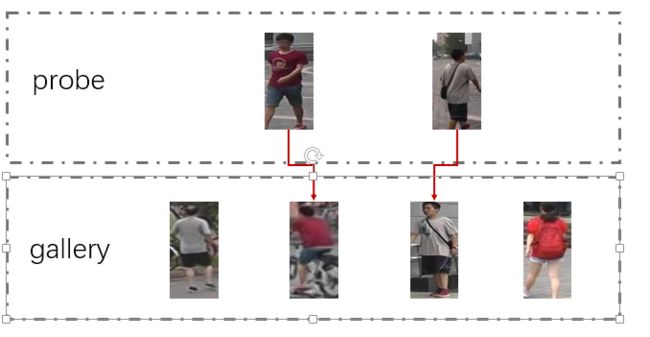
行人重识别(Person Re-identification)是一个图像检索问题,给定一组图片集(probe),对于probe中的每张图片,从候选图片集(gallery)中找到最可能属于同一个行人的图片。
行人重识别数据集是由一系列监控摄像头拍摄得到,并用检测算法将行人抠出,做行人的匹配。在这些数据集中,人脸是十分模糊的,无法作为匹配特征,而且由于多个摄像头拍摄视角不同,同个人可能被拍到正面,侧面,背面,具有不同的视觉特征,因此是一个比较难的图像匹配问题。常用数据集有很多,可以在这个网站查到。
Related Work
行人重识别问题有以下几种常见的解决方案:
基于视觉的行人重识别
这类方法通常提取行人图像特征,对特征进行距离度量,从而判断是否是同一个人。
有监督学习
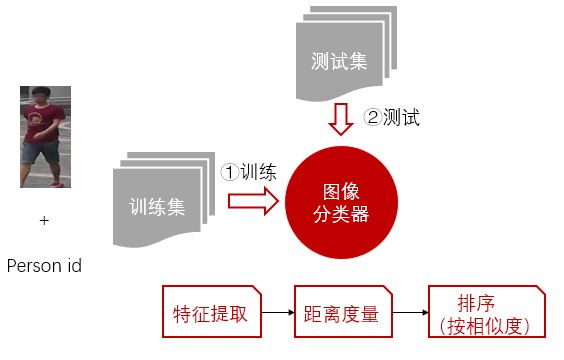
这类方法通常需要提供行人图片和行人id标签(person1,person2等),训练模型,提取图像特征,根据两张图特征的距离大小(可以用余弦距离,欧氏距离之类的计算),为probe中的每张图和gallery中的每张图计算其相似度,根据相似度将gallery中的图片排序,排序越高越可能为同一个人。
这方面的论文代表有TOMM2017: A Discriminatively Learned CNN Embedding for Person Re-identification,我们采用的基础图像分类器就是基于这篇论文用Keras实现的,后面细讲。
无监督学习
在CVPR2018之前,Person Reid领域正式发表的无监督工作只有CVPR2016的UMDL:Unsupervised Cross-Dataset Transfer Learning for Person Re-identification,基于字典学习方法,在多个源数据集上学习跨数据集不变性字典,迁移到目标数据集上。然而准确率依然很低。
结合摄像头拓扑的行人重识别
行人图片是摄像头拍到的,摄像头之间有一定的距离,行人的移动有一定的速度限制,因此行人在摄像头间的移动时间就会呈现出一定规律,比如,AB摄像头间有10米,人行走速度2m/s,如果AB摄像头在1s内捕捉到了两张图片,则这两张图片不可能是同一个人的,因此我们可以利用摄像头拓扑约束来提升行人重识别的准确率。
然而,这类方法往往有以下缺陷:
- 有些方法需要预先知道摄像头拓扑(AB摄像头之间的距离)
- 有些方法可以根据拍摄到的图像数据推断出摄像头拓扑,但是需要图像有标注(是否是同一个人)
- 即使推断出摄像头拓扑,与图像的融合结果依然很差
迁移学习
迁移学习现在是深度学习领域很常用的一个套路了,在源数据集上预训练,在目标数据集上微调,从而使得源数据集上的模型能够适应目标场景。这方面的论文代表有前面讲的UMDL,和Deep transfer learning person re-identification,然而,目前的迁移学习大多需要标签,而无监督迁移学习效果又很差,仍然有很大提升空间。
更多关于Person Reid的内容可以看一下我在博客写的几篇调研
Motivation
- 现有的行人重识别数据集中是否包含时空信息?包含的话是否存在时空规律?
- 缺乏两个时空点是否属于同一行人这种标签时,如何挖掘时空信息,构建时空模型?
- 如何融合两个弱分类器?有监督的融合有boosting算法可以用,无监督呢?
- 在缺乏标签的条件下,如何进行有效的迁移学习?
对应有三个创新点
- 无监督的时空模型构建
- 基于贝叶斯推断的时空图像模型融合
- 基于Learning to Rank的迁移学习
接下来详细解析我们的方法。
时空模型
数据集中的时空规律
所谓时空模型,即一个摄像头网络中,行人在给定两个摄像头间迁移时间的分布。
我们看遍所有Reid数据集,发现有三个数据集有时空信息,Market1501, GRID, DukeMTMC-ReID,其中,DukeMTMC-ReID是2017年后半年才出来的,时间比较仓促在论文中就没有包含跟它相关的实验。Market1501是一个比较大的Person Reid数据集,GRID是一个比较小的Person Reid数据集,并且都有六个摄像头(GRID中虽然介绍了8个摄像头,实际上只有6个摄像头的数据)。
例如,Marke1501中一张图片的时空信息是写在图片名字中的:
0007_c3s3_077419_03.jpg:
- 0007代表person id,
- c3代表是在3号摄像头拍到的,也就是空间信息,
- s3代表属于第3个时间序列(GRID和DukeMTMC中没有这个序列的信息,在Market1501中,不同序列的属于不同起始时间的视频,同一系列不同摄像头的视频起始时间相近),
- 077419为帧号,也就是时间信息。
我想吐槽的是,其实时空信息是非常容易保存的,只要知道图片是在什么时候,哪台摄像机上拍摄,就能够将时空信息记录并有效利用起来,希望多模态数据融合得到更多重视之后,做数据集的人能够更加重视可保存的信息吧。
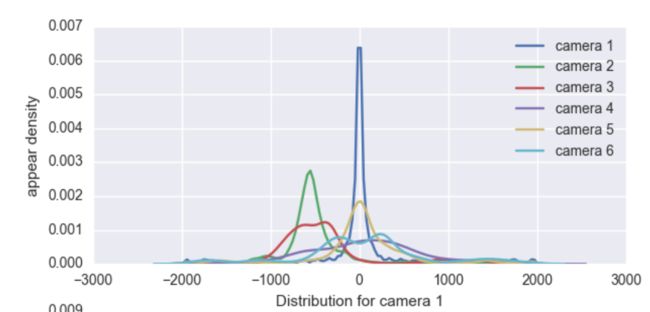
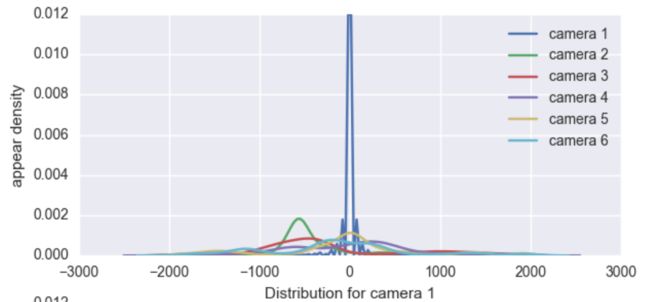
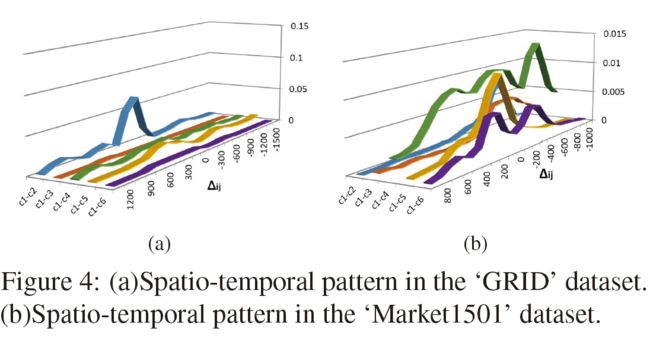
我们首先通过Market1501中的真实行人标签,计算训练集中所有图片对对应的时空点对对应的迁移时间,这里可视化了从摄像头1出发的行人,到达其他摄像头需要的时间的分布。
可以看到,到达不同目标摄像头的峰值位置不同,其中从摄像头1到摄像头1,意味着被单个摄像头拍到连续多帧,所以峰值集中在0附近,从摄像头1到摄像头2,峰值集中在-600附近,意味着大部分人是单向从摄像头2运动到摄像头1,等等,并且,说明这个数据集中存在显著可利用的时空规律。
无监督的时空模型构造
我们将迁移时间差命名为delta,这样说起来方便(装逼)一点。
如果我们能够统计一个数据集中的所有delta,给定一个新的delta(两个新的图片对应的两个时空点算出来的),我们能够用极大似然估计,用在这个delta前后一定范围(比如100帧)的delta的出现频率(=目标范围delta数量/总的delta数量),作为新时间差出现的概率,也就是两个时空点是同一人产生的概率。
但是!问题是我们在目标场景上往往是没有行人标记数据的!
于是我们就思考,
- 我们能不能根据两个时空点对应的两张图是否属于同一个人,来决定两个时空点是否属于同一个人?
- 而两张图是否属于同一个人,其实是一个图像匹配的二分类问题,我们可以用一些视觉模型来做,
- 但是这种视觉模型往往是需要有标签训练的,无标签的视觉模型往往比较弱
- 视觉模型弱没关系!我们相信跟时空模型结合就能变成一个强大的分类器!要有信仰!
- 只要我们能无监督地把时空模型构造出来,结合弱的图像分类器,因为加了时空信息,一定能吊打其他无监督模型!
思路有了,实现就很自然了,
- 我们先在其他数据集上(于是我们就可以说这是一个跨数据集的任务了)预训练一个卷积神经网络,
- 然后用这个卷积神经网络去目标数据集上提特征,
- 用余弦距离算特征相似度
- 将相似度排在前十的当做同一个人
- 用这种“同一个人”的信息+极大似然估计构造时空模型
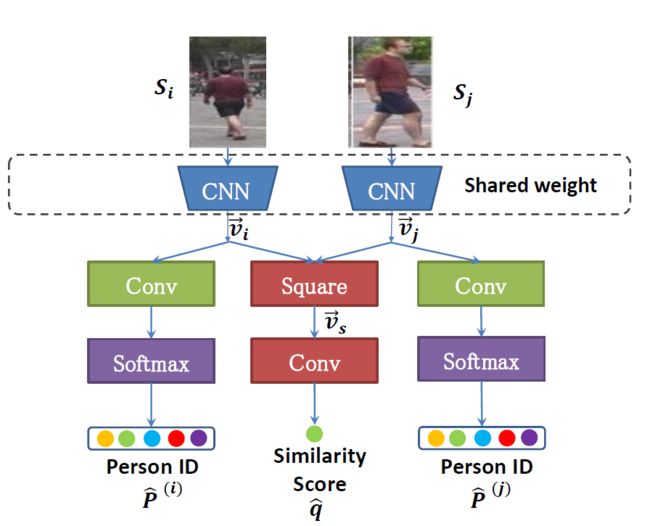
图像分类器上,我们这里用的是LiangZheng的Siamese网络,他们的源码是用MATLAB实现的,我用Keras复现了一把:
时空模型的极大似然估计可以看这里
聪明的读者应该会注意到,这个图像分类器是在其他数据及上预训练的,由于特征空间中数据分布不同,这个图像分类器太弱了,对于目标数据集来说,前十里会有许多错的样本,导致构造出来的时空模型和真实的时空模型有偏差
可以看到,构造的模型跟真实的模型还是有些差别的,但是峰值位置还是差不多,一定程度上应该还能用,但我们还是希望构造的模型尽量接近真实模型的。
于是我们开始思考
- 导致模型出现偏差的因素是什么?是错误的样本对
- 如何去掉错误样本对的影响?我们能不能把错误的样本对分离出来?没有标签咋办?
- (灵光一闪)错误的样本不就跟我瞎选的差不多?那我是不是可以随机地选样本对,算一个随机的delta分布出来
- 将估算的delta分布去掉随机的delta分布,剩下的多出来的部分,就是由于正确的行人迁移产生的,不就得到真实的delta分布了?
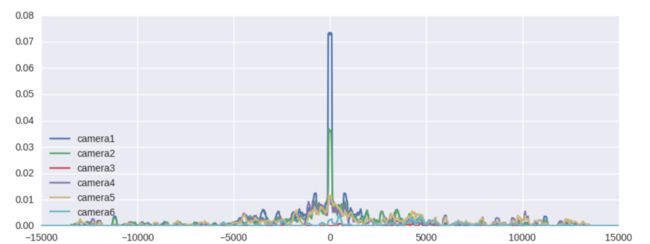
于是我们可视化了一下随机的delta分布
可以发现,
- 确实与估计模型和真实模型不同
- 存在较多抖动
这种随机的时间差分布也呈现出一定的集中趋势,其实体现的是采样的时间差分布,如,在1号摄像头采的图片大多在某个时间段,2号摄像头也大多在这个时间段采,但3号摄像头的图片大多是在其他时间段采到的。
考虑到时间差的频率图有这么多的抖动,我们在计算某个区域的时间差时,加上了均值滤波,并且做了一定区域的截断,包括概率极小值重置为一个最小概率值,时间差极大值重置为一个最大时间差。
接下来,应该怎么把错误的模型从估计的模型滤掉呢?又怎么将时空模型和图像模型结合呢?
基于贝叶斯推断的模型融合
首先看时空模型和图像模型的融合, 我们有一个视觉相似度Pv,一个时空概率Pst,一个直观的想法是,联合评分可以是Pv * Pst,如果要再抑制随机的评分Prandom,可以做个除法,就是Pv * Pst / Prandom
这样一看,像不像条件概率公式?于是我们开始推导(大量公式预警):
先看看我们手上的资源:现在我们有一个弱的图像分类器,可以为两张图片提取两个视觉特征vi, vj, 有两个时空点,空间特征为两个摄像头编号ci, cj,时间特征为两张图片拍摄的时间差∆ij,假定两张图对应的person id分别为Pi, Pj,那么我们的目标就是求,在给定这些特征的条件下,两张图属于同一个人的概率
Pr(Pi=Pj|vi,vj,ci,cj,∆ij)(论文公式6)
由条件概率公式P(A|B) = P(B|A)*P(A)/P(B),可得
Pr(Pi=Pj|vi,vj,ci,cj,∆ij)
= Pr(vi,vj,ci,cj,∆ij|Pi=Pj) *Pr(Pi=Pj)/ Pr(vi,vj,ci,cj,∆ij)
由时空分布和图像分布的独立性假设(长得像的人运动规律不一定像),我们可以拆解第一项,得到
= Pr(vi,vj|Pi=Pj) * Pr(ci,cj,∆ij|Pi=Pj) * Pr(Pi=Pj)/ Pr(vi,vj,ci,cj,∆ij)
其中Pr(Pi=Pj)是一个不好求的项,我们试着把它换掉,
先交换顺序(乘法交换律)
= Pr(vi,vj|Pi=Pj) * Pr(Pi=Pj) * Pr(ci,cj,∆ij|Pi=Pj) / Pr(vi,vj,ci,cj,∆ij)
由条件概率公式P(A|B)* P(B) = P(B|A) * P(A)可得
= Pr(Pi=Pj|vi,vj) * Pr(vi=vj)*Pr(ci,cj,∆ij|Pi=Pj) / Pr(vi,vj,ci,cj,∆ij)
可以看到
- Pr(Pi=Pj|vi,vj)可理解为两张图从视觉特征相似度上判定为同一人的概率
- Pr(ci,cj,∆ij|Pi=Pj)就是两个时空点是同一个人移动产生的概率
再次利用时空分布和图像分布的独立性假设,拆解分母
= Pr(Pi=Pj|vi,vj) * Pr(vi=vj)* Pr(ci,cj,∆ij|Pi=Pj) / Pr(vi,vj) * P(ci,cj,∆ij)
约掉Pr(vi=vj),
= Pr(Pi=Pj|vi,vj) * Pr(ci,cj,∆ij|Pi=Pj) /P(ci,cj,∆ij)
也就是
= 视觉相似度*同一人产生这种移动的概率/任意两个时空点组成这种移动的概率
这也就是论文公式(7),也就是我们一开始的猜想:Pv * Pst / Prandom
看着好像很接近我们手头掌握的资源了,但是,
- 我们并不知道理想的两张图的视觉相似度 Pr(Pi=Pj|vi,vj) ,只有我们的图像分类器判定的两张图的视觉相似度 Pr(Si=Sj|vi,vj) ,
- 我们并不能计算同一人产生这种移动的真实概率Pr(ci,cj,∆ij|Pi=Pj) ,我们只有依据视觉分类器估算的时空概率Pr(ci,cj,∆ij|Si=Sj) ,
- 我们倒是确实有数据集中任意两个时空点产生这种移动的概率P(ci,cj,∆ij)
于是我们想用Pr(ci,cj,∆ij|Si=Sj) ,P(ci,cj,∆ij)去近似,得到
= Pr(Si=Sj|vi,vj) * Pr(ci,cj,∆ij|Si=Sj) /P(ci,cj,∆ij)
看到这里其实就大致理解我们的融合原理了,实际上我们大部分实验也是用的这个近似公式算的。
实现上,先模拟两个时空模型,计算图像相似度,然后代入公式求融合评分,具体可以实现看我GitHub
但这个近似能不能做呢?我们来做一下误差分析(大量推导,不感兴趣可以跳到接下来出现的第二张图,不影响后面的理解,只是分析一波会更加严谨)。
实际上,误差是由图像分类器引入的,假设图像分类器判定两张图是同一个人的错判率为Ep,图像分类器判定两张图不是同一人的错判率为En,
则有,
Ep = Pr(Pi≠Pj|Si=Sj)(论文公式1)
En = Pr(Pi=Pj|Si≠Sj)(论文公式2)
则Pr(Pi=Pj|vi,vj) 与 Pr(Si=Sj|vi,vj) 的关系可以表示为:
Pr(Pi=Pj|vi,vj)
= Pr(Pi=Pj|Si=Sj) * Pr(Si=Sj|vi,vj) + Pr(Pi=Pj|Si≠Sj) * Pr(Si≠Sj|vi,vj)
= (1-Ep) * Pr(Si=Sj|vi,vj) + En * (1-Pr(Si=Sj|vi,vj) )
= (1-Ep-En) * Pr(Si=Sj|vi,vj) + En (论文公式8)
推导,Pr(ci,cj,∆ij|Pi=Pj) 和Pr(ci,cj,∆ij|Si=Sj) 的关系(这个没法像视觉相似度那样直接推导,因为因果关系不同)
Pr(ci,cj,∆ij|Si=Sj)
= Pr(ci,cj,∆ij|Pi=Pj) * (Pr(Pi=Pj)|Si=Sj) + Pr(ci,cj,∆ij|Pi≠Pj) * (Pr(Pi=Pj)|Si≠Sj)
= Pr(ci,cj,∆ij|Pi=Pj) * (1- Ep) + Pr(ci,cj,∆ij|Pi≠Pj) * Ep
同样可以得到
Pr(ci,cj,∆ij|Si≠Sj)
= Pr(ci,cj,∆ij|Pi=Pj) * En + Pr(ci,cj,∆ij|Pi≠Pj) * (1 - Ep)
联立上面两个式子解方程,消掉Pr(ci,cj,∆ij|Si≠Sj) 可以得到
Pr(ci,cj,∆ij|Pi=Pj)
= (1 - Ep - En)-1(1-En) * Pr(ci,cj,∆ij|Si=Sj) - Ep * Pr(ci,cj,∆ij|Si≠Sj) (论文公式5)
其中有个新概念Pr(ci,cj,∆ij|Si≠Sj) ,意味着图像分类器认为不是同一个人的时候,这种时空点出现的概率,实现上也不难,统计视觉相似度top10以后的点对应的时间差,作为反时空概率模型即可。
我们把两个近似(公式5和公式8)代进公式7,
可以得到
Pr(Pi=Pj | vi, vj, ∆ij, ci, cj)
= (M1 + En/(1 - En - Ep))((1-En)M2 - EpM3)/Pr(∆ij, ci, cj))(论文公式9)
其中,
M1 = Pr(Si=Sj|vi,vj),视觉相似度
M2 = Pr(∆ij,ci,cj|Si=Sj),正时空概率模型
M3 = Pr(∆ij,ci,cj|Si≠Sj),反时空概率模型
分母Pr(∆ij, ci, cj))为随机概率模型
以上四项都是可以从无标签目标数据集中结合图像分类器求解到的,并且,当En=Ep=0时(意味着图像分类器完全准确),这个公式可以退化为近似解:
Pr(Si=Sj|vi,vj) * Pr(ci,cj,∆ij|Si=Sj) /P(ci,cj,∆ij)
到这里,你是不是以为我们就可以用公式9算融合评分了?非也,公式9中,还有个问题:Ep,En是未知的!
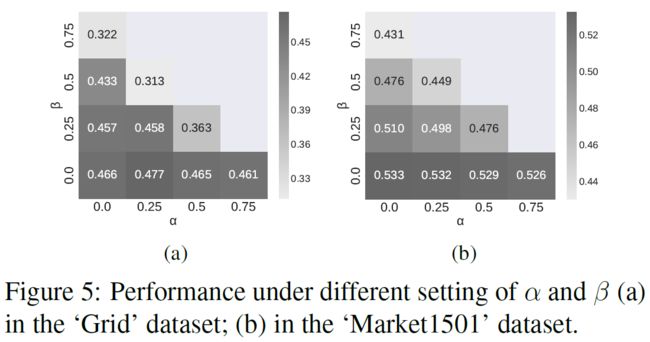
如果想要正儿八经地算Ep,En,要求目标数据集有标签,然后我们用图像分类器先算一遍,数数哪些算错了,才能把Ep,En算出来。因此我们用两个常数α和β分别替代Ep,En,整个模型的近似就都集中在了这两个常数上。
在论文Table1,2,3,4,Fig6相关的实验中,α=β=0,并且,在Fig5中,我们设置了其他常数来检查模型对于这种近似的敏感性
可以看到,虽然α和β较大时,准确率会有所下降,但是仍然能保持一定的水准,当你看到纯图像分类器的准确率之后,还会发现融合模型的准确率一直高于纯图像分类器。
你可能注意到了,图中α+β都是小于1的,这是因为,只有当Ep+En<1且α+β<1时,融合模型的Ep+En才会小于图像模型的Ep+En,说人话就是,只有图像模型不是特别糟糕,且近似的参数也比较正常的时候,融合模型才会比单个的图像模型要准,融合才有意义。这个定理的具体的证明放到论文附录里了,有兴趣的可以邮件私信我拿附录去看,这里摆出来就太多了。
于是我们得到了一个由条件概率推断支撑的多模态数据融合方法,称为贝叶斯融合
看一眼融合得到的时空分布图:
再从数据上看一眼融合的模型有多强:
| 源数据集 | 目标数据集 | 纯 | 图像 | 结果 | 融合 | 时空 | 结果 | |
|---|---|---|---|---|---|---|---|---|
| rank-1 | rank-5 | rank-10 | rank-1 | rank-5 | rank-10 | |||
| CUHK01 | GRID | 10.70 | 20.20 | 23.80 | 30.90 | 63.70 | 79.10 | |
| VIPeR | GRID | 9.70 | 17.40 | 21.50 | 28.40 | 65.60 | 80.40 | |
| Market1501 | GRID | 17.80 | 31.20 | 36.80 | 49.60 | 81.40 | 88.70 | |
| GRID | Market1501 | 20.72 | 35.39 | 42.99 | 51.16 | 65.08 | 70.04 | |
| VIPeR | Market1501 | 24.70 | 40.91 | 49.52 | 56.18 | 71.50 | 76.48 | |
| CUHK01 | Market1501 | 29.39 | 45.46 | 52.55 | 56.53 | 70.22 | 74.64 |
可以看到,
- 跨数据集直接迁移效果确实很差
- 融合之后的准确率Rank1准确率变成2-4倍
说明这种融合方式是确实行之有效的。
基于Learning to Rank的迁移学习
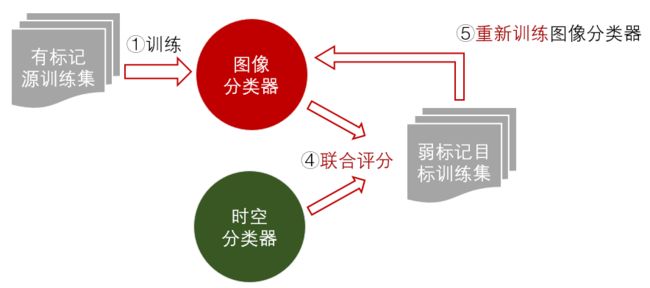
前面讲到图像分类器太弱了,虽然融合后效果挺好的(这个时候我们其实想着要不就这样投个NIPS算了),但是如果能提升图像分类器,融合的效果理论上会更好。而现在我们有了一个强大的融合分类器,我们能不能用这个融合分类器为目标数据集的图片打标签,反过来训练图像分类器呢?
一个常用的无监督学习套路就是,根据融合评分的高低,将图片对分为正样本对和负样本对(打伪标签),然后喂给图像分类器学习。
我们也尝试了这种做法,但是发现,数据集中负样本远远多于正样本,融合分类器分对的负样本是挺多的,但是分对的正样本超级少,分错的正样本很多,错样本太多,训练出来效果极差,用上一些hard ming的技巧也不行。
于是我们思考,
- 我们无法提供正确的01标签,分类器就只能学到许多错的01标签
- 我们是否可以提供一些软标签,让分类器去学习回归两个样本之间的评分,而不是直接学习二分类的标签?
- 这是一个图像检索问题,我们能不能用信息检索中的一些学习方法来完成这个任务?
于是自然而然地想到了Learning to Rank
Ranking
- 问题定义:给定一个对象,寻找与其最相关的结果,按相关程度排序
- 常用方法:
- Point-wise:每一个结果算一个绝对得分,然后按得分排序
- Pair-wise:每两个结果算一下谁的得分高,然后按这个相对得分排序
- List-wise:枚举所有排列情况,计算综合得分最高的一种作为排序结果
综合得分往往需要许多复杂的条件来计算,不一定适用于我们的场景,所以排除List-wise,Point-wise和Pair-wise都可以采用,得分可以直接用融合评分表示,Pair-wise可以用一组正序样本,一组逆序样本,计算两个得分,算相对得分来学习,有点Triplet loss的意味,于是在实验中采用了Pair-wise方法。
Pair-wise Ranking
- 给定样本xi,其排序得分为oi,
- 给定样本xj,其排序得分为oj,
- 定义oij=oi - oj,如果oij>0说明xi的排名高于xj,
- 将这个排名概率化,定义Pij = eoij/(1+eoij),为xi排名高于xj的概率。
- 对于任何一个长度为n的排列,只要知道n-1个相邻item的概率Pi,i+1,就可以推断出来任何两个item的排序概率
- 例如,已知Pik和Pkj,Pij = Pik * Pkj = eoik+okj/(1 + eoik+okj),其中oik=ln(Pik/(1 - Pik))
RankNet: Pair-wise Learning to Rank
RankNet是Pair-wise Learning to Rank的一种方法,用一个神经网络去学习输入的两个样本(还有一个query样本)与其排序概率(上面定义的)的映射关系。
具体到我们这个问题里
- 给定查询图片A,给定待匹配图片B和C
- 用神经网络预测AB之间的相似度Sab为B的绝对排序得分,计算AC之间的相似度Sac为C的绝对排序得分
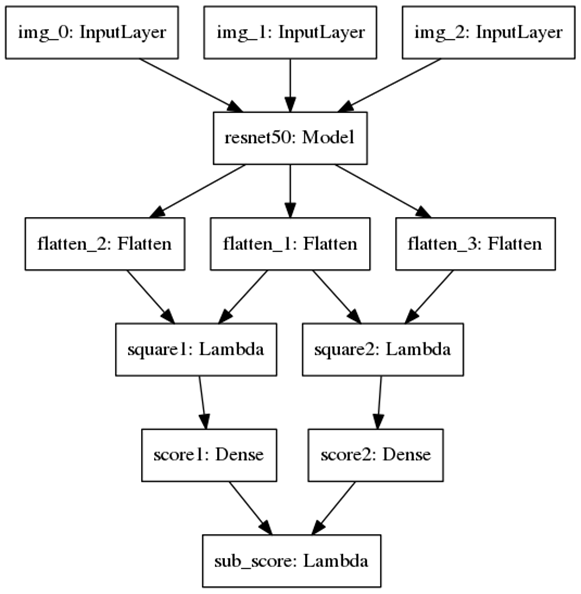
具体的神经网络用Keras实现并可视化出来长这样:
- 输入是三张图片,分别用Resnet52提取特征并flatten
- flatten之后写一个Lambda层+全连接层算特征向量带权重的几何距离,得到score1和score2
- 用score1和score2和真实分数算交叉熵Loss(下面讲)
- 则B排序高于C的概率为:
Pbc= eobc/(1+ eobc) = eSab- Sac / (1 + eSab- Sac)
- 用预测概率Pbc去拟合真实的排序概率,回归损失用预测概率和真实概率的交叉熵表达
C(obc) = -P'bcln Pbc - (1-P'bc)ln (1 - Pbc)
网络实现超级简单,主要麻烦在样本三元组构造
Transfer Learning to rank
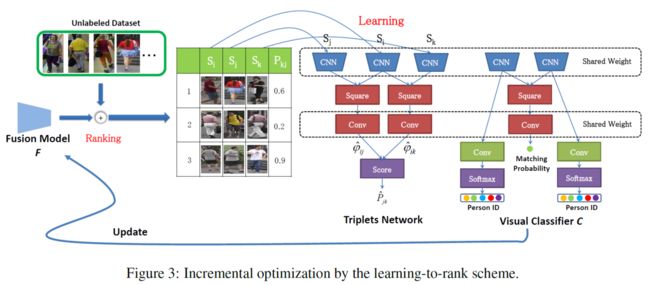
整个Learning to rank过程如图
我们用融合分类器为目标数据集中的图片对评分,构造三元组输入RankNet,其中Si是查询图,Sj是在与Si融合相似度top1 - top25中抽取的图片,Sk是在与Si融合相似度top25 - top50中抽取的图片,喂给RankNet学习,使得resnet52部分卷积层能充分学习到目标场景上的视觉特征。
Learning to Rank效果
| 源数据集 | 目标数据集 | 纯 | 图像 | 结果 | 融合 | 时空 | 结果 | |
|---|---|---|---|---|---|---|---|---|
| rank-1 | rank-5 | rank-10 | rank-1 | rank-5 | rank-10 | |||
| CUHK01 | GRID | 17.40 | 33.90 | 41.10 | 50.90 | 78.60 | 88.30 | |
| VIPeR | GRID | 18.50 | 31.40 | 40.50 | 52.70 | 81.70 | 89.20 | |
| Market1501 | GRID | 22.30 | 38.10 | 47.20 | 60.40 | 87.30 | 93.40 | |
| GRID | Market1501 | 22.38 | 39.25 | 48.07 | 58.22 | 72.33 | 76.84 | |
| VIPeR | Market1501 | 25.23 | 41.98 | 50.33 | 59.17 | 73.49 | 78.62 | |
| CUHK01 | Market1501 | 30.58 | 47.09 | 54.60 | 60.75 | 74.44 | 79.25 |
对比Learning to Rank前的效果,准确率都提升了,GRID数据集上提升尤为明显。
对比SOA有监督方法
一方面,我们将上面的跨数据集无监督算法应用在GRID和Market1501两个数据集上,与当前最好的方法进行对比,另一方面,我们还测试了有监督版本的效果,有监督即源数据集与目标数据集一致,如GRID预训练->GRID融合时空,效果如下:
- GRID
| Method | Rank 1 |
|---|---|
| JLML | 37.5 |
| TFusion无监督 | 60.4 |
| TFusion有监督 | 64.1 |
由于在这个数据集上时空规律十分明显(正确时间差都集中在一个很小的范围内),可以过滤掉大量错误分类结果,所以准确率甚至碾压了全部有监督方法。
- Market1501
| Method | Rank 1 |
|---|---|
| S-CNN | 65.88 |
| DLCE | 79.5 |
| SVDNet | 82.3 |
| JLML | 88.8 |
| TFusion无监督 | 60.75 |
| TFusion有监督 | 73.13 |
在Market1501这个数据集上,无监督的方法逼近2016年的有监督方法(我们的图像分类器只是一个ResNet52),有监督的方法超越2016年的有监督方法,虽然比不上2017年的有监督方法,但是如果结合其他更好的图像分类器,应该能有更好的效果。
对比SOA无监督方法
我们向UMDL的作者要到了代码,并复现了如下几组跨数据集迁移实验
| Method | Source | Target | Rank1 |
|---|---|---|---|
| UMDL | Market1501 | GRID | 3.77 |
| UMDL | CUHK01 | GRID | 3.58 |
| UMDL | VIPeR | GRID | 3.97 |
| UMDL | GRID | Market1501 | 30.46 |
| UMDL | CUHK01 | Market1501 | 29.69 |
| UMDL | VIPeR | Market1501 | 30.34 |
| TFusion | Market1501 | GRID | 60.4 |
| TFusion | CUHK01 | GRID | 50.9 |
| TFusion | VIPeR | GRID | 52.7 |
| TFusion | GRID | Market1501 | 58.22 |
| TFusion | CUHK01 | Market1501 | 59.17 |
| TFusion | VIPeR | Market1501 | 60.75 |
其中,UMDL迁移到Market1501的结果与悉尼科技大学hehefan与LiangZheng复现出来的效果差不多,所以我们的复现是靠谱的。
可以看到,无监督的TFusion全面碾压UMDL。
更多详细实验结果可以到论文中细看。
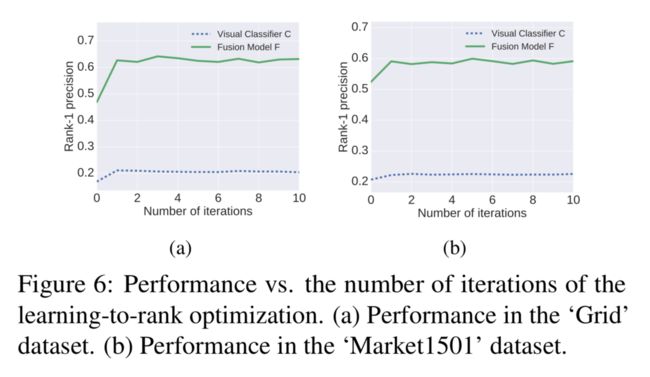
多次迭代迁移学习
回顾一下整个架构,我们用图像分类器估算时空模型,得到融合模型,用融合模型反过来提升图像分类器模型,图像分类器又能继续增强融合模型,形成一个闭环,理论上这个闭环循环多次,能让图像分类器无限逼近融合分类器,从而得到一个目标场景中也很强大的图像分类器,因此我们做了多次迭代的尝试:
在从目前的实验效果看,第一次迁移学习提升比较大,后面提升就比较小了,这个现象往好了说可以是收敛快,但往坏了说,虽然图像分类器得到了提升,但是没有出现图像分类器提升大于融合分类器的现象,所以这里边应该还有东西可挖。
后记
调研,可视化,找思路,找数据集,做实验,Debug,调参,写论文,九个月写一篇CVPR,这也是我们实验室第一篇CCF A类论文,算是来之不易的开山之作了。现在我们在Person Reid领域继续探索,正在搭建一个基于树莓派的摄像头网络,构造自己的数据集,并在这个基础上开展行人检测,多模态数据融合,轻量级深度模型,分布式协同终端,视频哈希,图像索引等一系列研究,欢迎follow我的Github,也欢迎持续关注我们实验室的博客
看了这么久,还不给我Github点star!