本文翻译自 Neural Networks : A 30,000 Feet View for Beginners
翻译:coneypo
在这篇文章中,我会向大家简要的介绍下 Neural Networks / 神经网络;
可以作为 Machine Learning / 机器学习 和 Deep Learning / 深度学习 的入门爱好者参考;
我们文章中会尽量用简短的,零基础的方式来向大家介绍。
作为 Black Box / 黑盒 的 Neural Networks / 神经网络
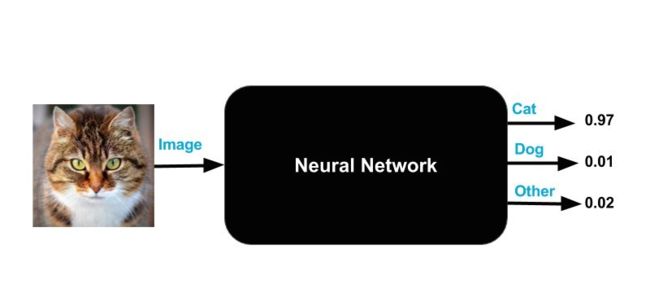
我们可以把神经网络当作一个神奇的黑盒子,你不必知道黑盒子里面是什么;
你现在只知道黑盒有 一个输入 和 三个输出;
输入可以是图像的尺寸,颜色或者种类等等;
输出分别为 "猫","狗",和 "其他" 三种标签,标签的输出值都是介于 0~1,而且三种标签的数值之和为 1。
理解神经网络的输出
黑盒的神奇之处其实很简单,如果你向它输入一张图像,它会输出三个数值;
一个理想化的完美神经网络,对于 "猫" 输出(1,0,0),对于 "狗" 输出(0,1,0),对于 "其他" 输出(0,0,1);
事实上即使一个训练的非常好的神经网络也可能达不到上述的完美输出;
比如,如果你输出一张猫的图像,”猫” 标签输出的数值为 0.97,“狗” 标签下的输出数值为 0.01,“其他” 标签下的输出数值为 0.02。
输出数值 可以理解为 可能性概率;
比如说黑盒 "认为" 这张图像是 "猫" 的概率是 97%,很小的概率是 "狗" 或者是 "其他" 物种;
请注意输出数值之和一定为 1;
具体的这种问题归类于 image classification / 图像分类 问题:给定一张图像,你用最有可能的标签去给图像进行分类(猫,狗,或者其他);
理解神经网络的输入
现在你作为一名程序员,你可以使用数值来表示神经网络的输出;
但是你如何输入一张图像呢?
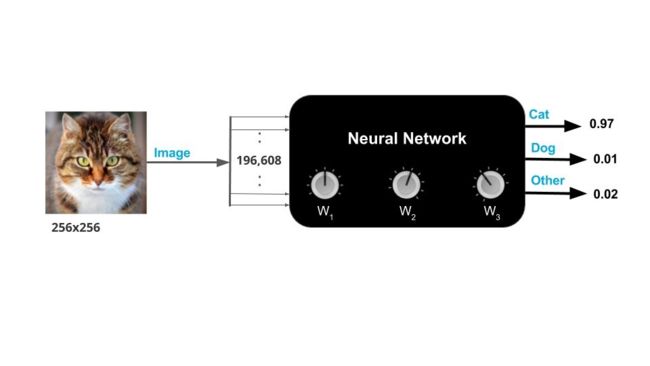
图像其实就是一个存放数值的数组。一个 256*256 三通道的图像其实就是 256*256*3=196608 个数值;
你使用图片浏览器来浏览 256*256 大小的图片,其实在内存里就是 196608 个数值构成的 continuous block / 连续块;
经过上述描述,我们知道输入有一点复杂,输入实际上有 196608 个数值,我们由此更新一下我们的黑盒模型。
我知道你在想什么,如果图像不是 256*256 的呢?
其实你可以通过以下步骤来把任何一张图像转换为 256*256 大小:
- Non-Square aspect ratio / 非正方形纵横比调整:如果输入图像不是正方形,你可以重新调整图像大小到 256,然后从图像中间裁剪出 256*256 的像素大小;
- Grayscale image / 灰度图:如果输入图像不是一个彩色图像,你可以通过拷贝灰度图到三个通道来获得三通道彩色图像;
大家使用很多不同种类的方法来转换图像到一个适合的尺寸( 比如 256*256 ),但是正如我之前所说,我会让我们的流程变得简单,我不会使用这些各种各样的方法。需要注意的事情是任何一张图像可以被转换成你想要的尺寸,即使我们在裁剪或者调整大小的时候丢掉一些信息。
训练神经网络需要注意什么
黑盒模型有一些 knobs / 旋钮 来调整模型参数;
从技术角度来说,这些旋钮称之为 weights / 权重;
当这些旋钮处于正确的位置,神经网络就可以达到更好更正确的输出结果;
训练神经网络就是要找到正确的 旋钮设置 / 权重;
如何训练神经网络
如果你有一个黑盒,但是不知道正确的旋钮设置,那么这个黑盒其实相当于没用的;
好消息是你可以通过训练神经网络来找到正确的旋钮设置。
训练神经网络和训练小孩特别像。你拿一个球给小孩看,然后告诉他这是一个球;
当你给他看了很多种球之后,小孩就会弄明白,球和球的形状有关,与它的颜色或者尺寸无关;
然后你给小孩一个鸡蛋,问他这是什么,他回答是球。你纠正他这不是球,这是鸡蛋;
当这个过程重复几次之后,这个小孩就可以辨别球和鸡蛋了。
为了训练一个神经网络,你给它几千个想让它学习的分类例子(比如猫,狗或者其他);
这种训练称之为 Supervised Learning / 监督学习,因为你提供给这个神经网络来自某个分类的图像,然后确切的告诉它,这张图像来自这个分类;
为了训练神经网络,我们需要三件事情:
1. Training data / 训练数据:
各种分类的数千张图像和它们期待的输出;
比如所有猫的图像,被期待输出为(1,0,0);
2. Cost function / 损失函数:
我们需要知道当前的权值设置是否比之前的设置要更好;
损失函数会统计训练集中所有图像经过神经网络处理的错误信息;
常用的损失函数被称为 sum of squared errors (SSE) / 平方误差和;
对于一张图像,你期待的输出是一只猫或者(1,0,0),神经网络的实际输出是(0.37,0.5,0.13),
平方损失会计算出所有图像的损失,都会被简化为平方误差之和;
训练的目的就是找到合适按钮设置(权重)达到最小化损失函数的目的。
3. How to update the knob setting / 如何调整权重:
最后我们需要根据观察训练图像的错误数据,来更新神经网络的权重;
用一个单独的 knob / 旋钮 来训练神经网络
我们现在有一千张猫的图像,一千张狗的图像,和一千张随机的物体不是猫也不是狗,这三千张图像就是我们的训练集;
如果神经网络还没有被训练,内部的权值是随机的,当你将三千张图像输入神经网络,得到输出的准确率为 1/3 ;
为了简化流程,我们的神经网络只有一个旋钮权值。由于我们已经仅仅有一个权值,我们可以测试一千种不同的权值测试,来找到可以最小化损失函数最好的权值设置。这样就完成了我们的训练;
然而,事实上神经网络不仅仅有一个旋钮权值,以流行的神经网络 VGG-Net 为例,它有 1.38 亿 个旋钮权值。
利用多个旋钮权值来训练神经网络
刚才我们用一个旋钮来训练神经网络,在测试完所有可能性(可能数量很大)之后,我们可以找到最好的参数设置;
这有点不切实际,因为如果三个旋钮权值,我们就要测试十亿次;
很明显这种暴力搜索方式是不切实际的;
幸运的是,有一种解决方法,当损失函数是 convex function / 凸函数 时(看起来像一个碗);
我们可以用 Gradient Descent / 梯度下降 的方式来迭代找到最好的权重;
Gradient Descent / 梯度下降
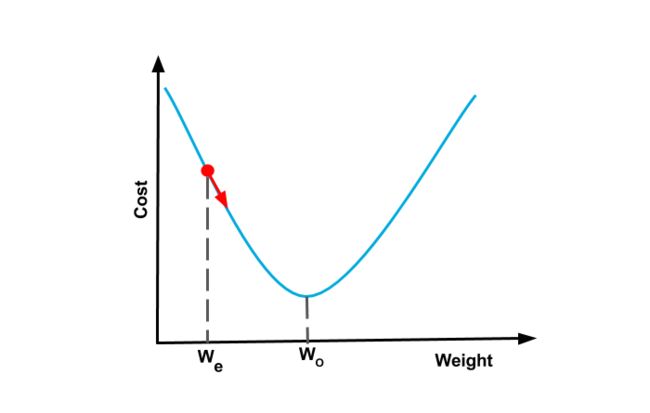
让我们回到只有一个权值的神经网络,并且假设我们现在的旋钮设置(或者权值)是 ![]() ;
;
如果我们的损失函数像一个碗,我们可以找到损失函数的斜率,然后一步步移到最佳的旋钮设置 ![]() , 这个过程称为 梯度下降;
, 这个过程称为 梯度下降;
因为我们根据斜率(或者 Gradient / 梯度)逐渐向下移动( Descending / 下降 ),当我们到达损失函数碗的底部,梯度或者斜率会变成零,然后完成你的训练;
这些碗形状的函数被称之为 convex functions / 凸函数。
但是第一次是如何估计?你可以选择一个随机数;
Note:当你使用一些流行的神经网络架构,比如 GoogleNet 或者 VGG-Net,你可以使用基于 ImageNet 训练的权重,而不是选择随机的初始权值,这样可以收敛的更快。
当有多个旋钮时,梯度下降也是相似的工作原理;
比如当有两个旋钮时,损失函数在 3D 坐标中看起来像一个碗一样;
如果你把一个球放到这个碗的任何位置,球会沿着 the maximum downward slope / 最大下降斜率 滚到碗的底部,这也是梯度下降工作的原理;
如果你让球以全速滚下去,它会到达底部,但是由于惯性和动能,还会继续向上滚动,最终停在底部;
但是如果给这个球下落的时候增加约束条件,让它更慢的下降,到达底部之后就不会再上升了,其实会花费更少的时间来达到底部;
实际上当我们训练一个神经网络的时候,我们使用一个参数 learning rate / 学习率 来控制收敛速度;
当我们有很多个纽扣(权重)时,损失函数的形状在更高维的空间,依然是一个碗形。虽然这时候这个碗很难去可视化观测,但是斜率和梯度下降依然可以工作;
因此梯度下降提供了一个很好的找到最小损失函数解决方案。
Backpropagation / 逆传播
有一个问题,知道了当前的权值设置,我们怎么知道损失函数的斜率?
损失函数的梯度取决于训练集中,真实输出和当前输出的差别;
换句话说,训练集的每张图像,如果神经网络在这些图像上表现的差,都会最终的梯度计算都有贡献。
用来估计损失函数的梯度的算法,被称为 Backpropagation / 逆传播。
我们会在将来的文章中介绍逆传播。
# 英文版权 @
# 翻译中文版权 @ coneypo
# 转载请注明出处