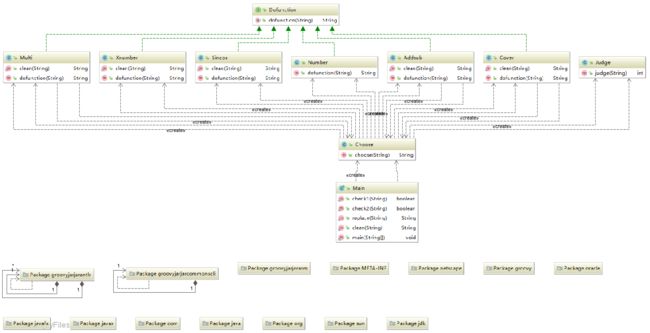
在本次博客的写作中,我运用IntelliJ旗舰版的Diagrams功能绘制类图,用MetricsReloaded插件进行代码复杂度分析。
Complexity Metrics(复杂度分析)
这部分我们需要使用的主要是方法和类的复杂度分析。
方法的复杂度分析主要基于循环复杂度的计算。循环复杂度是一种表示程序复杂度的软件度量,由程序流程图中的“基础路径”数量得来。
-
ev(G):即Essentail Complexity,用来表示一个方法的结构化程度,范围在$[1,v(G)]$之间,值越大则程序的结构越“病态”,其计算过程和图的“缩点”有关。
-
iv(G):即Design Complexity,用来表示一个方法和他所调用的其他方法的紧密程度,范围也在$[1,v(G)]$之间,值越大联系越紧密。
-
v(G):即循环复杂度,可以理解为穷尽程序流程每一条路径所需要的试验次数。
对于类,有OCavg和WMC两个项目,分别代表类的方法的平均循环复杂度和总循环复杂度。
Dependency Metrics(依赖度分析)
依赖度分析度量了类之间的依赖程度。有如下几种项目:
- Cyclic:指和类直接或间接相互依赖的类的数量。这样的相互依赖可能导致代码难以理解和测试。
- Dcy和Dcy:计算了该类直接依赖的类的数量,带表示包括了间接依赖的类。
- Dpt和Dpt:计算了直接依赖该类的类的数量,带表示包括了间接依赖的类。
(1)基于度量来分析程序结构
第一次作业:
类图:
度量:
优点:简单明了,写起来比较快
缺点:复用性不强
第二次作业:
类图:
度量:
优点:基于第一次作业的修改版本,仍然结构相对简单,易于上手
缺点:不用性仍然不强,只能在较小的范围内进行改动与功能拓展
第三次作业:
类图:
度量:
优点:采用循环、递归和接口,极大地提升了程序的可复用性,使得复杂的操作与识别步骤可以被逐步拆分成几个小块进行运算,增强了代码的逻辑性
缺点:在化简部分仍有待提高
(2)分析程序的bug
在这一单元的三次作业中,我的程序的bug主要由以下2种:
1.在程序设计中由于考虑不周全导致的处理、运行上的bug,具体表现为,一些合法的输入会引起我所写的程序的歧义、数组越界或爆栈。针对这一类bug,我的修正思路主要是:在设计程序结构时,进行细化思维,力求考虑周全;不同“层次”的问题归类进行比较和讨论,同类问题做相似的处理,避免出现错误或遗漏。
2.在写代码过程中手误敲出了bug,比如正则表达式可以匹配空格的问题。针对这一类bug,我的思路是在写代码时尽力认真细致,每写完一部分,就回过头去认真检查。
在公测和互测的过程中,除了以上2中类型的bug,还有2种bug,即在后续步骤中修改先前步骤保存的数值而造成的bug,以及在化简结构表达式时因考虑不周、化简错误而出现的bug。这需要我们在设计程序时,将执行不同功能的代码段化为小块,不同小块保持相对的独立性,不直接调用对方所存储的数据,而是通过数据接口进行传输;同时在写代码的任何环节,都要始终如一,考虑周全,起码要做到对结果式的情况的讨论不少于对输入表达式的讨论。
(3)发现别人程序bug所采用的策略
在互测为同组同学的代码找bug时,我主要从结构和功能的角度出发,先尝试多组我自己在写代码的过程中“设计”出的易于产生bug的数据,再细致考察对方代码的结构,着重寻找、分析他和我不同的部分。这样,即使找不到bug,也能在他人的思路中收获不少。
比如在此次第三次作业的互测阶段,我就是在第二次作业的基础上,分析从第二次作业到第三次作业有哪些改变,又有哪些沿袭的地方,再针对性地进行测试。同样,我会阅读他人的代码,结合被测程序的代码设计测试用例。
(4)Applying Creational Pattern
综合分析我的三次作业,我的前两次作业,因为在写代码时对“面向对象”概念的理解尚不明晰,加之当时的作业功能实现要求较低、代码的实现较为简单,所以并没有很好地进行类的设计和划分,导致程序的复用性不强,为第三次作业带来了一些麻烦。在完成第三次作业时,我主要运用了接口和递归嵌套的思想进行设计,对输入的求导式不断地进行拆分,直到得出能够直接写出导函数的“单项”,如x、x^2、sin(x)、cos(x^4)等,然后将每一层的导数返回给上一层,最后将整个求导式的导数返回到主函数中输出。