[AGC006E] Rotate 3x3 树状数组+贪心

Description

​ XFZ在北京一环内有一套房。

​ XFZ房子的地砖呈网格状分布，是一个3∗N3∗N的网格。XFZ在买下这套房时，每个地砖上有一个数字，位置为(i,j)(i,j)的地砖上的数字恰好为i+3(j−1)i+3(j−1)。

N=5N=5时XFZ家的俯视图

​ XFZ的房子特别高级，地底暗藏转轴机关。每次转轴可以顶起一片3x3的地砖，将其旋转180°，再放下地砖。

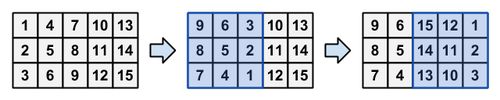
一个转轴作业的例子（蓝色区域为旋转完成之后的区域）

​ XFZ决定要让地砖有美感。他希望他能使用他的高级转轴达到一个目的：对于位置为(i,j)(i,j)的地砖，其数字恰好为ai,jai,j。其中aa是一个XFZ指定的3∗N3∗N的目标数组。

​

Input

​ 第一行一个正整数NN（5≤N≤1055≤N≤105）

​ 接下来3行，每行NN列，描述ai,jai,j（1≤ai,j≤3N1≤ai,j≤3N）

​ 保证所有的ai,jai,j互不相同。

Output

​ 如果XFZ的目标能够实现，输出“Yes”，否则输出“No”。二者皆不包含引号。

Sample Input

#Sample Input 1
5
9 6 15 12 1
8 5 14 11 2
7 4 13 10 3

#Sample Input 2
5
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15

#Sample Input 3
5
1 4 7 10 13
2 5 8 11 14
3 6 9 12 15

#Sample Input 4
6
15 10 3 4 9 16
14 11 2 5 8 17
13 12 1 6 7 18

#Sample Input 5
7
21 12 1 16 13 6 7
20 11 2 17 14 5 8
19 10 3 18 15 4 9

Sample Output

#Sample Output 1
Yes

#Sample Output 2
No

#Sample Output 3
Yes

#Sample Output 4
Yes

#Sample Output 5
No

HINT

​ 第一组样例对应着题目描述中使用的例子。

​ 第三组样例不需要任何操作，直接满足要求

本题采用subtask。

存在10%10%的数据满足n≤8n≤8。

Sol

首先意识到奇偶列是独立的

然后我们发现这个东西：

• a b c d e

• C B A d e

• C B E D a

• e b c D a

• e b A d C

• a B E d C

• a B c D e (1)

• a d C b e

• c D A b e

• c B a d e

• A b C d e (2)

这说明我们可以凭空去翻转一种数的连续两列（奇数或者偶数），所以限制条件变成了偶数列翻转量和奇数列移动量、奇数列翻转量和奇数列移动量必须是同奇或者同偶才能实现，毕竟两种东西是捆绑的。。。而且上面的要求是偶数个奇偶，奇数是没有办法的。。。所以差必须是偶数才能得到同奇同偶。

做的时候先特判一些傻逼情况，判完之后分奇偶进行，用树状数组维护区间右移个数（类似冒泡排序的交换），然后每次\(O(logn)\)进行一次对某一列的复位并计算移动量（翻转量输入的时候就能判定）。

Code

#include 
using namespace std;
int n,a[3][100005],b[5],mov[2],rev[2],should[100005],now[100005],s[100005];
void upd(int x,int y){for(;x;x-=x&-x) s[x]+=y;}
int que(int x){int a=0;for(;x<=n;x+=x&-x) a+=s[x];return a;}
int main()
{
    scanf("%d",&n);
    for(int i=0;i<3;i++) for(int j=1;j<=n;j++) scanf("%d",&a[i][j]);
    for(int i=1;i<=n;i++)
    {
        b[0]=a[0][i];b[1]=a[1][i];b[2]=a[2][i];sort(b,b+3);
        if(b[2]%3||b[0]+1!=b[1]||b[1]+1!=b[2]||b[1]!=a[1][i]||(i-b[2]/3)%2) return puts("No"),0;
        should[i]=b[2]/3;rev[i%2]=(rev[i%2]+(a[0][i]>a[2][i]))%2;now[should[i]]=i;
    }
    for(int i=1;i<=n;i++,i++)
    {
        int nex=now[i]+2*que(now[i]);
        mov[1]=(mov[1]+abs(i-nex)/2)%2;upd(now[i],1);
    }
    memset(s,0,sizeof(s));
    for(int i=2;i<=n;i++,i++)
    {
        int nex=now[i]+2*que(now[i]);
        mov[0]=(mov[0]+abs(i-nex)/2)%2;upd(now[i],1);
    }
    if(mov[0]!=rev[1]||mov[1]!=rev[0]) puts("No");
    else puts("Yes");
}

转载于:https://www.cnblogs.com/CK6100LGEV2/p/9489664.html