题目描述
如图,设一个圆分成 n 个扇形 S1 ... ,Sn (扇形大小不一样),现用 k 种不同的颜色对这 n 个扇形进行染色 ( n>=3 , k>=3 );
每一个扇形染一种颜色,相邻的 (即有公共边的) 扇形染不同的颜色,试求共有多少种染色方法.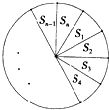
--2005全国高中数学联赛
输入输出格式
输入 :
两个整数 n 和 k (0 <= n,k <= 1000)
输出 :
最多的方案种数, 答案对 19260817 取模
样例数据
input#1:
3 5
output#1
60
Solution
思路有误! 之后会 更新.
这道题感觉上和 HNOI 2008 越狱差不多.
我们令 :
\[a^{n}_{m}\]
为 一个长度为n的序列 里面有m种颜色时满足条件的方案数.
同时,我们通过 越狱 这道题,可以知道 其中合法情况即为:
\[ a^{n}_{m} =n*(n-1)^{m-1}\]
接下来,我们先假设当前这个圆为一个序列,那么我们满足的答案即为\[ a^{n}_{k} \]
但是我们会发现,如果说单纯当作一个数列来处理的话,我们会有重复的情况:
即首位与末位的颜色相同此时我们作为一个圆的话,是不满足条件的.
那么我们可以换一个角度,我们可以把末位和首位的两个元素看为一个元素.
那么此时,在这种情况下的合法情况即为我们上一次求解的多余的.因为此时的首位和末位正好是相同的.
那么此时我们就可得到答案为:
\[ a^{n}_{k}-a^{n-1}_{k} \]
于是即可求解.
代码 :
#include
using namespace std;
long long n,m,p;
long long quick_pow(long long s,long long ks)
{
if(ks==1)return s%p; long long k=s; ks--;
while(ks>0)
{
if(ks%2==1)k=(k*s)%p;
ks/=2;
s=(s*s)%p;
}return k%p;
}
int main()
{
cin>>n>>m;
p=19260817;
int old=(m*quick_pow(m-1,n-1)%p+p)%p;
int duo=(m*quick_pow(m-1,n-2)%p+p)%p;
cout<<(old-duo+p)%p<