歇了几天了,没有写博客。从今天开始要总结树和二叉树了。那么什么是树呢?
1,树的定义:
1)有且仅有一个特定的称为根Root的结点。
2)当n>1时,其余结点可分为m(m>0)个互不相交的有限集,其中每个集合本身又是一个棵树,并称为根的子树。
2,树的表示方法:
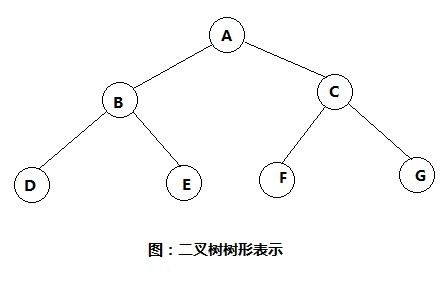
最常见的是树形表示法和广义表表示法,下面是树形表示法,如图所示。
上图的广义表表示法为:(A(B(D,E),C(F,G)))
3,常见的术语:
1) 父节点,孩子节点,兄弟节点。以上图为例,A是B和C的父节点,B和C是A的孩子节点,B和C之间就是兄弟节点了。
2) 结点的度和树的度。结点的度即结点有几个分支,比如节点A有两个分支B和C,那么结点A的度就是2,树的度即为一棵树中结点的最大度数,所以树的度也是2。
3) 有序树和无序树。如果将树中结点的子树看成是从左至右依次有序且不能交换,则称该树为有序树,否则称为无序树。
4) 森林。在上图中,如果将根节点A拿掉,那么B和C子树合并就是森林了。
5) 二叉树。二叉树是一种特殊的树。它的每个结点至多只有两棵子树。
4,二叉树的常见性质:
性质1 在二叉树的第i层上至多有2i-1个结点(i>=1)
性质2 深度为k的二叉树至多有2k-1个结点(k>=1)
性质3 满二叉树,在一棵深度为k且有2k-1个结点。完全二叉树,若一棵深度为k的二叉树,其前k-1层是一个棵满二叉树,而最下面一层(即第k层)上的结点都集中在该层最左边的若干位置上。
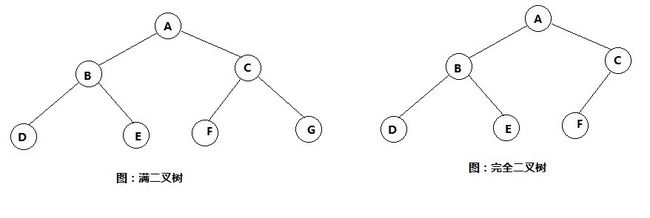
满二叉树一定是完全二叉树,但是完全二叉树则不一定是满二叉树。
下面是满二叉树和完全二叉树图示。
5,二叉树的两种存储结构
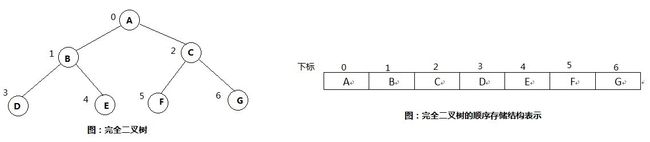
1) 顺序存储
对于完全二叉树而言,可以使用顺序存储结构。但是对于一般的二叉树来说,使用存储结构会有两个缺点,一,如果不是完全二叉树,则必须将其转化为完全二叉树,二是增加了很多虚节点,浪费资源空间。
2) 链式存储
这是最常用的一种二叉树存储结构。每个结点设置三个域,即值域,左指针域和右指针域,用data表示值域,lchild和rchild分别表示指向左右子树的指针域。如图所示。
6,二叉树的常见操作
1) 插入节点
思路:首先找到要插入节点的父节点,然后确定插到父节点的左边还是右边,最后将节点插入。
2) 查找节点
思路:运用递归查找。
3) 计算树的深度
思路:分别递归左子树和右子树,取长度较大的那一个作为整个树的深度。
4) 遍历之先序遍历
思路:先访问根,然后遍历左子树,再遍历右子树
5) 遍历之中序遍历
思路:先遍历左子树,再访问根,最后遍历右子树
6) 遍历之后序遍历
思路:先遍历左子树,再遍历右子树,最后访问根
7) 遍历之层次遍历
思路:从上到小,从左到右遍历
下面是算法实现代码。
C#版:
namespace DS.BLL { ////// 描述:二叉树操作类 /// 作者:鲁宁 /// 时间:2013/9/5 11:36:43 /// public class BinTreeBLL { //按层遍历的存储空间长度 public static int Length { get; set; } /// /// 生成根节点 /// /// public static BinTree<string> CreateRoot() { BinTree<string> root = new BinTree<string>(); Console.WriteLine("请输入根节点,以便生成树"); root.Data = Console.ReadLine(); Console.WriteLine("根节点生成成功"); return root; } /// /// 插入节点 /// /// 待操作的二叉树 /// 插入节点后的二叉树 public static BinTree<string> Insert(BinTree<string> tree) { while (true) { //创建要插入的节点 BinTree<string> node = new BinTree<string>(); Console.WriteLine("请输入待插入节点的数据"); node.Data = Console.ReadLine(); //获取父节点数据 Console.WriteLine("请输入待查找的父节点数据"); var parentNodeData = Console.ReadLine(); //确定插入方向 Console.WriteLine("请确定要插入到父节点的:1 左侧, 2 右侧"); Direction direction = (Direction)Enum.Parse(typeof(Direction), Console.ReadLine()); //插入节点 tree = InsertNode(tree,node,parentNodeData,direction); //todo:没有找到父节点没有提示??? if (tree == null) { Console.WriteLine("未找到父节点,请重新输入!"); continue; } Console.WriteLine("插入成功,是否继续? 1 继续,2 退出"); if (int.Parse(Console.ReadLine()) == 1) continue; else break; //退出循环 } return tree; } public static BinTree InsertNode (BinTree tree, BinTree node, T parentNodeData, Direction direction) { if (tree == null) return null; //找到父节点 if (tree.Data.Equals(parentNodeData)) { switch (direction) { case Direction.Left: if (tree.Left != null) throw new Exception("左节点已存在,不能插入!"); else tree.Left = node; break; case Direction.Right: if (tree.Right != null) throw new Exception("右节点已存在,不能插入!"); else tree.Right = node; break; } } //向左子树查找父节点(递归) InsertNode(tree.Left,node,parentNodeData,direction); //向右子树查找父节点(递归) InsertNode(tree.Right,node,parentNodeData,direction); return tree; } /// /// 查找节点 /// /// 节点数据类型 /// 二叉树 /// 要查找的节点数据 /// 要查找的节点 public static bool GetNode (BinTree tree, T data) { if (tree == null) return false; //查找成功 if (tree.Data.Equals(data)) return true; //递归查找 return GetNode(tree.Left,data); //这里有问题??? } /// /// 获取二叉树的深度 /// 思路:分别递归左子树和右子树,然后得出较大的一个即为二叉树的深度 /// /// 二叉树的数据类型 /// 待操作的二叉树 /// 二叉树的深度 public static int GetLength (BinTree tree) { if (tree == null) return 0; int leftLength, rightLength; //递归左子树的深度 leftLength = GetLength(tree.Left); //递归右子树的深度 rightLength = GetLength(tree.Right); if (leftLength > rightLength) return leftLength + 1; else return rightLength + 1; } /// /// 先序遍历 /// 思路:输出根节点--->遍历左子树--->遍历右子树 /// /// 二叉树的数据类型 /// 待操作的二叉树 public static void Traversal_DLR (BinTree tree) { if (tree == null) return; //输出节点的值 Console.Write(tree.Data+"\t"); //递归遍历左子树 Traversal_DLR(tree.Left); //递归遍历右子树 Traversal_DLR(tree.Right); } /// /// 中序遍历 /// 思路:遍历左子树--->输出根节点--->遍历右子树 /// /// /// public static void Traversal_LDR (BinTree tree) { if (tree == null) return; //遍历左子树 Traversal_LDR(tree.Left); //输出节点的值 Console.Write(tree.Data + "\t"); //遍历右子树 Traversal_LDR(tree.Right); } /// /// 后序遍历 /// 思路:遍历左子树--->遍历右子树--->输出根节点 /// /// /// public static void Traversal_LRD (BinTree tree) { if (tree == null) return; //遍历左子树 Traversal_LRD(tree.Left); //遍历右子树 Traversal_LRD(tree.Right); //输出节点的值 Console.Write(tree.Data + "\t"); } /// /// 按层遍历 /// 思路:从上到下,从左到右遍历节点 /// /// /// public static void Traversal_Level (BinTree tree) { if (tree == null) return; int head=0; int tail=0; //申请保存空间 BinTree [] treeList=new BinTree [Length]; //将当前二叉树保存到数组中 treeList[tail] = tree; //计算tail的位置 tail = (tail + 1) % Length; //除留余数法 while (head != tail) { var tempNode=treeList[head]; //计算head的位置 head = (head + 1) % Length; //输出节点的值 Console.Write(tempNode.Data+"\t"); //如果左子树不为空,则将左子树保存到数组的tail位置 if (tempNode.Left != null) { treeList[tail] = tempNode.Left; //重新计算tail的位置 tail = (tail + 1) % Length; } //如果右子树不为空,则将右子树保存到数组的tail位置 if (tempNode.Right != null) { treeList[tail] = tempNode.Right; //重新计算tail的位置 tail = (tail + 1) % Length; } } } /// /// 清空 /// 思路:使用递归释放当前节点的数据值 /// /// /// public static void Clear (BinTree tree) { if (tree == null) return; //递归左子树 Clear(tree.Left); //递归右子树 Clear(tree.Right); //释放节点数据 tree = null; } } /// /// 二叉树(二叉链表)存储结构 /// /// public class BinTree { public T Data { get;set;} //数据域 public BinTree Left { get; set; } //左孩子 public BinTree Right { get; set; } //右孩子 } /// /// 插入方向(左节点还是右节点) /// public enum Direction { Left=1, Right=2 } } namespace BinTree.CSharp { class Program { static void Main(string[] args) { Console.WriteLine("***************二叉树(二叉链表)********************"); //创建根节点 BinTree<string> tree = BinTreeBLL.CreateRoot(); //插入节点 Console.WriteLine("\n*********插入节点***********"); BinTreeBLL.Insert(tree); //先序遍历 Console.WriteLine("\n先序遍历结果:"); BinTreeBLL.Traversal_DLR(tree); //中序遍历 Console.WriteLine("\n中序遍历结果:"); BinTreeBLL.Traversal_LDR(tree); //后序遍历 Console.WriteLine("\n后序遍历结果:"); BinTreeBLL.Traversal_LRD(tree); //层次遍历 Console.WriteLine("\n层次遍历结果:"); BinTreeBLL.Length = 50; BinTreeBLL.Traversal_Level(tree); //获取树的深度 Console.WriteLine("\n当前树的深度为:{0}",BinTreeBLL.GetLength(tree)); Console.ReadKey(); } } }
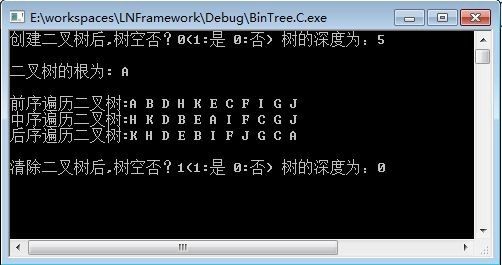
程序输出结果如图:
C语言版:
#include "string.h" #include "stdio.h" #include "stdlib.h" #include "io.h" #include "math.h" #include "time.h" #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 #define MAXSIZE 100 /* 存储空间初始分配量 */ typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ /**********定义二叉树的存储结构************/ typedef char TElemType; TElemType Nil=' '; /* 字符型以空格符为空 */ typedef struct BinTreeNode /* 结点结构 */ { TElemType data; /* 结点数据 */ struct BinTreeNode *lchild,*rchild; /* 左右孩子指针 */ }BinTreeNode,*BinTree; /*****************************************/ /***********用于构造二叉树************** */ int index=1; typedef char charArray[24]; /*声明一个char类型数组,charArray是数组名也是一个指针*/ charArray str; Status AssignStr(charArray T,char *chars) { int i; if(strlen(chars)>MAXSIZE) return ERROR; /*输入字符的长度超过存储空间最大值*/ else { T[0]=strlen(chars); /*0号单元存放字符串长度*/ for(i=1;i<=T[0];i++) { T[i]=*(chars+i-1); /*???*/ } return OK; } } /* ************************************* */ /*构造二叉树*/ void CreateBinTree(BinTree *T) { TElemType ch; ch=str[index++]; if(ch=='#') *T=NULL; else { *T=(BinTree)malloc(sizeof(BinTreeNode)); if(!*T) exit(OVERFLOW); (*T)->data=ch; /* 生成根结点 */ CreateBinTree(&(*T)->lchild); /* 构造左子树 */ CreateBinTree(&(*T)->rchild); /* 构造右子树 */ } } /* 构造空二叉树*/ Status InitBinTree(BinTree *T) { *T=NULL; return OK; } /*清空二叉树*/ void ClearBinTree(BinTree *T) { if(*T) { if((*T)->lchild) /* 有左孩子 */ ClearBinTree(&(*T)->lchild); /* 销毁左孩子子树 */ if((*T)->rchild) /* 有右孩子 */ ClearBinTree(&(*T)->rchild); /* 销毁右孩子子树 */ free(*T); /* 释放根结点 */ *T=NULL; /* 空指针赋0 */ } } /*判断二叉树是否为空*/ Status IsBinTreeEmpty(BinTree T) { if(T) return FALSE; else return TRUE; } /*计算二叉树的深度*/ int GetDepth(BinTree T) { int i,j; if(!T) return 0; if(T->lchild) i=GetDepth(T->lchild); else i=0; if(T->rchild) j=GetDepth(T->rchild); else j=0; return i>j?i+1:j+1; } /*获取二叉树的根节点*/ TElemType GetRoot(BinTree T) { if(IsBinTreeEmpty(T)) return Nil; /*Nil表示空字符*/ else return T->data; } /*前序遍历 思路:访问根节点--->前序遍历左子树--->前序遍历右子树 */ void PreOrderTraverse(BinTree T) { if(T==NULL) return; printf("%c ",T->data);/* 显示结点数据,可以更改为其它对结点操作 */ PreOrderTraverse(T->lchild); /* 再先序遍历左子树 */ PreOrderTraverse(T->rchild); /* 最后先序遍历右子树 */ } /*中序遍历 思路:中序遍历左子树--->访问根节点--->中序遍历右子树 */ void InOrderTraverse(BinTree T) { if(T==NULL) return; InOrderTraverse(T->lchild); /* 中序遍历左子树 */ printf("%c ",T->data);/* 显示结点数据,可以更改为其它对结点操作 */ InOrderTraverse(T->rchild); /* 最后中序遍历右子树 */ } /*后序遍历 思路:后序遍历左子树--->后序遍历右子树--->访问根节点 */ void PostOrderTraverse(BinTree T) { if(T==NULL) return; PostOrderTraverse(T->lchild); /* 先后序遍历左子树 */ PostOrderTraverse(T->rchild); /* 再后序遍历右子树 */ printf("%c ",T->data);/* 显示结点数据,可以更改为其它对结点操作 */ } int main() { int i; BinTree T; TElemType e1; /*初始化二叉树为一棵空树*/ InitBinTree(&T); /*设置字符数组用于构造二叉树*/ AssignStr(str,"ABDH#K###E##CFI###G#J##"); /*创建二叉树*/ CreateBinTree(&T); printf("创建二叉树后,树空否?%d(1:是 0:否) 树的深度为:%d\n",IsBinTreeEmpty(T),GetDepth(T)); /*获取二叉树的根节点*/ e1=GetRoot(T); printf("\n二叉树的根为: %c\n",e1); /*前序遍历*/ printf("\n前序遍历二叉树:"); PreOrderTraverse(T); /*中序遍历*/ printf("\n中序遍历二叉树:"); InOrderTraverse(T); /*后序遍历*/ printf("\n后序遍历二叉树:"); PostOrderTraverse(T); /*清空二叉树*/ ClearBinTree(&T); printf("\n\n清除二叉树后,树空否?%d(1:是 0:否) 树的深度为:%d\n",IsBinTreeEmpty(T),GetDepth(T)); i=GetRoot(T); if(!i) printf("树空,无根\n"); getchar(); }