Andrew Ng机器学习编程作业:K-means Clustering and Principal Component Analysis

作业文件

machine-learning-ex7

1. K-means聚类

在这节练习中，我们将实现K-means聚类，并将其应用到图片压缩上。我们首先 从二维数据开始，获得一个直观的感受K-means算法是如何工作的。之后我们将K-means算法应用到图片压缩上，通过减少出现在图片上的颜色的数量。

1.1 实现K-means

K-means算法是一种聚类算法，自动将相似的的数据聚成一类。具体来说，给定一个数据集，我们想要将这些数据集聚成一个个簇，K-means的一个直观理解就是从猜测初始聚类中心开始，迭代将样本点分配给最近的中心点，然后通过对应的同类样本点重新计算聚类中心。

K-means的算法步骤如下

% Initialize centroids
centroids = kMeansInitCentroids(X, K);
for iter = 1:iterations
    % Cluster assignment step: Assign each data point to the
    % closest centroid. idx(i) corresponds to c^(i), the index
    % of the centroid assigned to example i
    idx = findClosestCentroids(X, centroids);

    % Move centroid step: Compute means based on centroid
    % assignments
    centroids = computeMeans(X, idx, K);
end

算法的内部循环重复执行下面两步

1. 把每个样本点指定给离它最近的聚类中心

2.使用分配给聚类中心的点计算这些点的平均值，并指定为新的聚类中心。

K-means算法总会收敛到一些聚类中心。注意收敛结果可能不会很理想，结果有初始化的聚类中心有关。因此，在实际境况中，K-means算法经常使用不同的初始化的聚类中心运行。从这些不同初始化的聚类结果中选择比较好的结果的方式是选择有最低代价函数值的结果。

1.1.1 寻找最近的聚类中心

K-means算法迭代过程的第一步是把每个样本点指定给最近的聚类中心。给定当前的聚类中心，我们需要将每个每个样本设置为：

ci是离xi最近的聚类中心的索引。是第j个聚类中心。

我们的任务是完成findClosestCentroids.m文件中的代码。此函数输入为数据矩阵X与所有聚类中心坐标，输出为一个一维数组，存储了样本点对应聚类的索引。

当我们完成后，运行下面代码，我们应该看到[1 3 2]对应前三个样本的所属聚类索引

findClosestCentroids.m中的代码：

for i = 1:size(X,1)
    min = (X(i,:)-centroids(1,:))*(X(i,:)-centroids(1,:))';
    for j = 1:K
        k = (X(i,:)-centroids(j,:))*(X(i,:)-centroids(j,:))';
        if min>=k
            idx(i) = j;
            min = k;
        end
    end
    
end

 

1.1.2 计算聚类中心

给定每个点对应的聚类后，下一步是重新计算聚类中心，具体来说新的聚类中心等于

是属于第k类的样本点，比如属于第2类，即k=2。则更新聚类中心。我们应该在computeCentroids.m中完成代码。

computeCentroids.m中代码为：

 

 

for i = 1:m
   centroids(idx(i),:) = centroids(idx(i),:)+X(i,:);
end
for i = 1:K
    centroids(i,:) = centroids(i,:)./length(find(idx==i));
end

1.2 K-means在样本数据集上运行

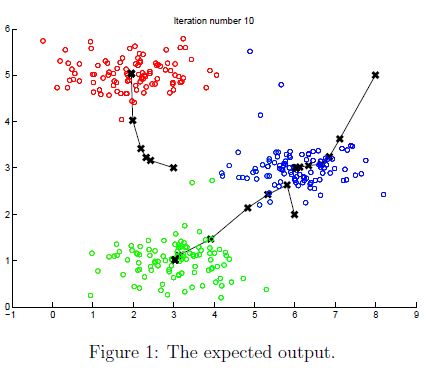
刚我们完成两个函数后（findClosestCentroids and computeCentroids），下面代码将会对2维数据将进行聚类。帮助我们理解K-mean是如何工作的。循行结果如图1所示

 

 

 

 1.3 随机初始化

随机初始化聚类中心的一个好的方法是，随机从样本点中原则初始聚类中心。初始化代码如下。

% Initialize the centroids to be random examples

%Randomly reorder the indicies of examples
randidx = randperm(size(X,1));
% Take the first K examples
centroids = X(randidx(1:K),:);

上面代码首先会将索引随机打乱。之后通过打乱后的索引选择前K个样本，这样会避免选择两个重复的样本作为初始聚类中心。

 1.4 使用K-means进行图片压缩

在这部分练习，我们将使用K-means算法进行图片压缩。一个由标准24位色彩表示的图片，每一个像素由3个8位无符号整数（范围位0-255）表示.代表红绿和蓝的颜色强度。这种编码通常称为RPG编码，我们的图像包含上千种颜色，在这节练习中，我们将减少颜色的种类到16种，通过减少颜色种类，实现图片压缩。

 

 在这一节练习，我们将使用K-means算法选择16个颜色用来代表压缩的图片。具体来说我们将原始图像的每个像素点代表一个数据样本，并使用K-means算法来找到16种颜色。当我们在图片上完成聚类，我们就可以使用16种颜色来替换图片种的颜色。

1.4.1 K-means应用在像素上

在MATLAB中，图片可以通过如下加载

A = imread('bird_small.png');

读入后会形成一个三维矩阵A，前两维为像素点的位置，第三维为代表红色，绿色，或者蓝色，比如A（50, 33, 3），给定在50行，33列的蓝色的强度。下面代码首先会加载图片，然后生成一个m*3的像素颜色矩阵。m=128*128，然后使用K-means处理这个矩阵。

%  Load an image of a bird
A = double(imread('bird_small.png'));
A = A / 255; % Divide by 255 so that all values are in the range 0 - 1

% Size of the image
img_size = size(A);

将图片转化为一个N*3的像素矩阵，每行包含红色，绿色与蓝色的值。这将作为我们K-means算法的输入。

X = reshape(A, img_size(1) * img_size(2), 3);

执行我们的K-means算法，我们应该尝试使用不同的聚类数目K值，与最大迭代次数 max_iters 

K = 16;
max_iters = 10;

当使用K-means算法时，我们应该进行随机初始化聚类中心，我们在执行下面代码前应该先完成 kMeansInitCentroids.m。

initial_centroids = kMeansInitCentroids(X, K);

% Run K-Means
[centroids, ~] = runkMeans(X, initial_centroids, max_iters);

在找到16个颜色后，我们现在可以指定每个像素给其最近的聚类中心通过使用findClosestCentroids函数。这样我们就能使用中心点来代表原图像的每个像素。注意原图像的每个像素点的大小为24，所以整个图片的大小为

新表示出来的图像需要以字典形式额外存储这16种颜色，每个要求24位。但是图像本身的每个像素仅需要4位来表示颜色。因此最终每个图像的大小为对应于将原始图像压缩大约6倍。

% Find closest cluster members
idx = findClosestCentroids(X, centroids);

 

 

 

 

 最终我们可以看到通过聚类中心点代表原始图像像素的压缩效果。具体来说我们用聚类中心的颜色替换了每个对应像素的颜色。

基本上，我们现在已经将图像X表示成了idx的索引。我们可以将idx索引代表的颜色映射到每个像素来恢复图像。

X_recovered = centroids(idx,:);

% Reshape the recovered image into proper dimensions
X_recovered = reshape(X_recovered, img_size(1), img_size(2), 3);

% Display the original image 
figure;
subplot(1, 2, 1);
imagesc(A); 
title('Original');
axis square

% Display compressed image side by side
subplot(1, 2, 2);
imagesc(X_recovered)
title(sprintf('Compressed, with %d colors.', K));
axis square

 2. 主成分分析（PCA)

这部分练习我们将通过使用主成分分析法来进行降维。我们首先以2维数据实验看PCA是如何工作的。之后我们将把PCA应用在5000张人脸图像上。

2.1 样本数据集

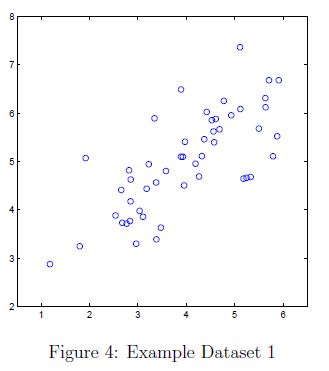
为了帮助我们理解PCA是如何工作的。我们首先从2维数据集开始，数据集如图4所示

在这部分练习，我们将看到使用PAC将2D变为1D将会发生什么。在实践种，我们可能想要将数据从256维减少到50维，但是使用低维度的数据可以让我们更好的理解这个算法。

2.2 实现PCA

在这部分练习我们将实现PAC，PCA有两个实现步骤。首先计算数据的协方差矩阵，接着，使用MATLAB svd函数计算特征值。这些将对应数据变化的主要成分。在使用PCA之前，首先用数据减去均值规范化数据集。接着放缩维度使他们在共同的范围内。下面代码已经使用featureNormalize 函数进行了规范化。

在规范化数据后，我们就可以执行PCA来计算主成分了。我们的任务是完成 pca.m的代码。我们首先应该计算数据集的协方差矩阵。

X是数据矩阵，每行代表一个样本。m是样本的数量，注意∑是n*n的矩阵，而不是求和运算符。

在计算玩协方差矩阵后，我们可以使用SVD来计算主成分了。在MATLAB中SVD的命令如下。

U包含主成分，S是一个对角矩阵。一旦我们完成了pca.m，下面代码将会将会在数据集上执行PCA，并且将找到的对应主成分画出。如图5所示。脚本还会输出第一个特征向量，我们将看到输出结果[-0.707 -0.707]。（可能MATLAB会输出负的结果，因为是同样有效的选择）

pca.m内的代码

X = 1/m*(X'*X);
[U,S] = svd(X);

 

 执行代码

% Before running PCA, it is important to first normalize X
[X_norm, mu, ~] = featureNormalize(X);

% Run PCA
[U, S] = pca(X_norm);

% Draw the eigenvectors centered at mean of data. These lines show the directions of maximum variations in the dataset.
hold on;
drawLine(mu, mu + 1.5 * S(1,1) * U(:,1)', '-k', 'LineWidth', 2);
drawLine(mu, mu + 1.5 * S(2,2) * U(:,2)', '-k', 'LineWidth', 2);
hold off;

2.3 使用PCA进行降维

在计算主成分后，我们可以使用主成分来减少特征的维度，通过将每个样本投到低维的空间。在这部分练习，我们将使用PCA返回的特征向量，将样本集映射到低维空间。

在实践中，如果我们使用了线性回归，或神经网络等算法，我们可以使用映射后的数据集代替原始数据集，通过使用映射后的数据集我们可以将模型训练的更快，因为输入了更少的维度。

2.3.1 将数据集映射到主成分上

我们应该完成projectData.m内的代码，具体来说，给定一个数据集X，和一个主成分U，以及我们想要减少到的维度K，我们应该将每个样本X映射到前K个主成分U。注意前K个主成分U是指U的的前K列。因此U_reduce = U(:, 1:K).

完成projectData.m内的代码

Z = X*U(:,1:K);

2.3.2 返回到原数据的近似值

在把数据映射到低维空间后，我们可以把数据投影到高维空间近似的恢复数据。我们的任务是完成 recoverData.m 中的代码，将每个样本K投影回原空间，并返回近似值。

recoverData.m的代码

X_rec = Z*U(:,1:K)';

2.3.3 可视化投影

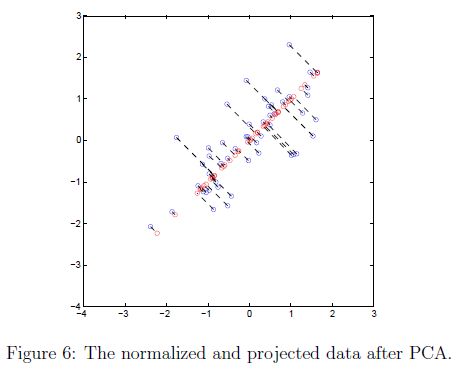
在完成projectData和 recoverData后，这部分代码将会同时展示投影和近似恢复数据来让我们了解投影是如何影响数据的。如图6所示，原始图像的点为蓝点，投影后的点为红点。给定U1，投影有效的保留了方向信息

2.4.1 PCA在面部应用

将PCA应用在面部数据集，我们首先规范化数据集通过每个特征数据减去对应的平均值。下面代码将会规范化数据，同时执行PCA。在运行PCA后，我们获得了数据的主成分。注意每个主成分在U中是一个行向量，长度为n。可以证明，我们可以通过重新组成32*32的矩阵对应与原始图像的，来可视化主成分。

下面代码展示了前36个主成分如图8.

[X_norm, ~, ~] = featureNormalize(X);

% Run PCA
[U, ~] = pca(X_norm);

% Visualize the top 36 eigenvectors found
displayData(U(:, 1:36)');

我们可以看到脸部一般的外貌轮廓然而细节丢失了。这可以显著的减少我们的数据大小，可以有效的加速学习。比如我们训练神经网络来实现人类识别，我们可以使用降维而不是原始图像。

X_rec  = recoverData(Z, U, K);

% Display normalized data
subplot(1, 2, 1);
displayData(X_norm(1:100,:));
title('Original faces');
axis square;

% Display reconstructed data from only k eigenfaces
subplot(1, 2, 2);
displayData(X_rec(1:100,:));
title('Recovered faces');
axis square;

2.5 可视化PCA

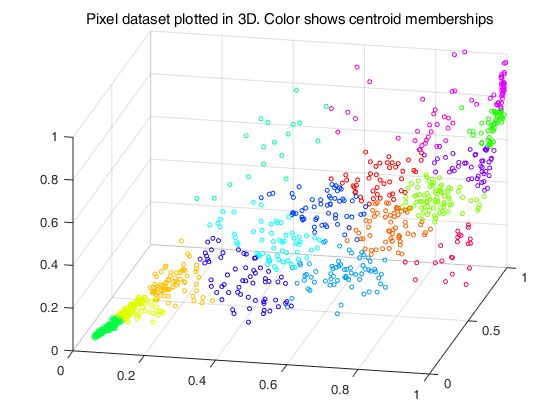
在前面的简单K-means实现图片压缩练习，我们使用了K-means算法在3维RGB空间让。现在我们提供可以最终可视化最终像素分配的3D空间的代码，每个点根据其所属聚类进行了着色。

A = double(imread('bird_small.png'));
A = A / 255;
img_size = size(A);
X = reshape(A, img_size(1) * img_size(2), 3);
K = 16; 
max_iters = 10;
initial_centroids = kMeansInitCentroids(X, K);
[centroids, idx] = runkMeans(X, initial_centroids, max_iters);

%  Sample 1000 random indexes (since working with all the data is
%  too expensive. If you have a fast computer, you may increase this.
sel = floor(rand(1000, 1) * size(X, 1)) + 1;

%  Setup Color Palette
palette = hsv(K);
colors = palette(idx(sel), :);

%  Visualize the data and centroid memberships in 3D
figure;
scatter3(X(sel, 1), X(sel, 2), X(sel, 3), 10, colors);
title('Pixel dataset plotted in 3D. Color shows centroid memberships');

 

 

在三维数据或更高的维度上可视化数据是很麻烦的，因此，在2维空间上可视化是很值得的，即使损失了一些信息。在实践中，PCA通常用于减少数据的维度以用于可视化。下面代码，脚本将会通过PCA将3维数据减少到2维。并可视化2维散点图，可以将PCA投影视为旋转，选择可以最大平铺数据的角度，集最佳视角。

% Subtract the mean to use PCA
[X_norm, mu, sigma] = featureNormalize(X);

% PCA and project the data to 2D
[U, S] = pca(X_norm);
Z = projectData(X_norm, U, 2);

% Plot in 2D
figure;
plotDataPoints(Z(sel, :), idx(sel), K);
title('Pixel dataset plotted in 2D, using PCA for dimensionality reduction');

 

转载于:https://www.cnblogs.com/lolybj/p/10130688.html