（13）Go实现线段树-数组实现

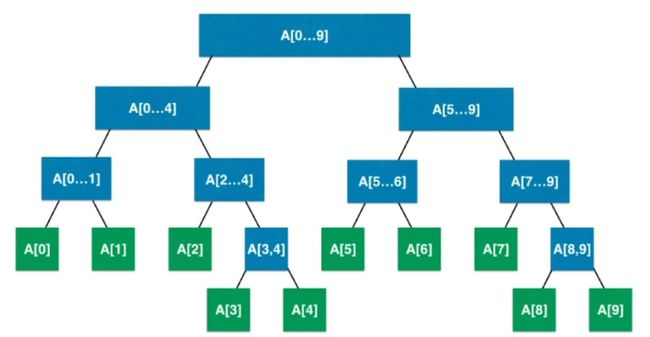
线段树，也叫区间树，segmengt-tree，是一种长度不变的平衡树结构，父节点存储的结果是左右子节点的总计。
以数组arrs求和为例子：
1）每个父节点存储的都是所有子节点的总和
2）所有叶子节点均为arrs的单个元素值
如下图

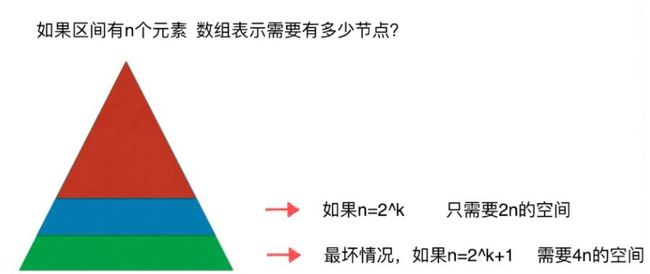
问：数组arrs有n个元素，依此创建的线段树需要由多少个节点？
//
答：需要4n的空间，解答如下图

使用线段树时，不考虑添加元素，一般采用4n的静态空间即可

问：为什么要使用线段树？
答：在区间统计，区间染色这类区间不变的问题中，线段树更好高快速的解决问题。
    在基于线段树的更新和查询中，时间复杂度都能达到O(logn)

// TODO: 基于数组实现的线段树
type segmentTree struct {
    tree   []int    //线段树
    data   []int    //数组数据
    merger func(v1, v2 int) int    //线段树功能函数，如求和，求余等等
}

func leftChild(i int) int {
    return 2*i + 1
}

// 传入一个数组arrs和一个功能函数func,根据功能函数返回一个线段树
func NewSegmentTree(arrs []int, merger func(i1, i2 int) int) *segmentTree {
    length := len(arrs)

    tree := &segmentTree{
        tree:   make([]int, length*4),
        data:   arrs,
        merger: merger,
    }
    tree.bulidSegmentTree(0, 0, length-1)

    return tree
}

// 在tree的index位置创建 arrs [ l 到 r ]  的线段树
func (tree *segmentTree) bulidSegmentTree(index, l, r int) int {
    // 递归终止条件
    if l == r {
        tree.tree[index] = tree.data[l]
        return tree.data[l]
    }

    // 递归过程
    leftI := leftChild(index)
    rightI := leftI + 1
    mid := l + (r-l)/2
    leftResp := tree.bulidSegmentTree(leftI, l, mid)
    rightResp := tree.bulidSegmentTree(rightI, mid+1, r)

    tree.tree[index] = tree.merger(leftResp, rightResp)
    return tree.tree[index]
}

// 查询arrs范围queryL到queryR 的结果
func (tree *segmentTree) Query(queryL, queryR int) (int, error) {
    length := len(tree.data)
    if queryL < 0 || queryL > queryR || queryR >= length {
        return 0, errors.New(
            "index  is illegal ")
    }
    return tree.queryrange(0, 0, length-1, queryL, queryR), nil
}

// 在以index为根的线段树中[l...r]范围里，搜索区间[queryL...queryR]的值
func (tree *segmentTree) queryrange(index, l, r, queryL, queryR int) int {
    if l== queryL && r== queryR {
        return tree.tree[index]
    }

    leftI := leftChild(index)
    rightI := leftI + 1
    mid := l+ (r-l)/2

    if queryL > mid {
        return tree.queryrange(rightI, mid+1, r, queryL, queryR)
    }
    if queryR <= mid {
        return tree.queryrange(leftI, l, mid, queryL, queryR)
    }

    leftResp := tree.queryrange(leftI, l, mid, queryL, mid)
    rightResp := tree.queryrange(rightI, mid+1, r, mid+1, queryR)
    return tree.merger(leftResp, rightResp)
}

// 更新data中索引k的值为v
func (tree *segmentTree) Update(k, v int) {
    length := len(tree.data)
    if k < 0 || k >= length {
        return
    }
    tree.set(0, 0, length-1, k, v)
}

// 在以treeIndex为根的线段树中更新index的值为e
func (tree *segmentTree) set(treeIndex, l, r, k, v int) {
    if l == r {
        tree.tree[treeIndex] = v
        return
    }

    leftI := leftChild(treeIndex)
    rightI := leftI + 1
    midI := l + (r-l)/2

    if k > midI {
        tree.set(rightI, midI+1, r, k, v)
    } else {
        tree.set(leftI, l, midI, k, v)
    }

    tree.tree[treeIndex] = tree.merger(tree.tree[leftI], tree.tree[rightI])
}

func (tree *segmentTree) Print() {
    fmt.Println(tree.tree)
}

测试线段树
func multiplication(v1, v2 int) int {
    return v1 * v2
}

func main() {
    c := []int{-1, 1, 2, -3, 4, 5, 6}

    a := segment_tree1.NewSegmentTree(c, multiplication)
    a.Print()

    resp, err := a.Query(2, 5) //-120
    fmt.Printf("查询结果:%d,  错误:%v\n", resp, err)

    a.Update(2, -2)
    a.Print()
}

测试结果
[720 6 120 -1 -6 20 6 -1 1 2 -3 4 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
查询结果:-120,  错误:
[-720 -6 120 -1 6 20 6 -1 1 -2 -3 4 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]

相关：
用线段树解决leetcode-307题目：区间索引和检索
https://www.jianshu.com/p/fc53b9ff0a80

有bug欢迎指出，转载请注明出处。