提要

本文先介绍光线追踪的理论,然后着重一步一步来搭建渲染场景,从最基本的向量类开始.采用的语言是c++,利用面向对象的思想,一些基础的线性代数和空间几何的知识也会用到，编程的框架用的是GLFW，渲染用到的是OpenGL。


原理

光线追踪，简单地说，就是从摄影机的位置，通过影像平面上的像素位置(比较正确的说法是取样(sampling)位置)，发射一束光线到场景，求光线和几何图形间最近的交点，再求该交点的著色。如果该交点的材质是反射性的，可以在该交点向反射方向继续追踪。光线追踪除了容易支持一些全局光照效果外，亦不局限于三角形作为几何图形的单位。任何几何图形，能与一束光线计算交点(intersection point)，就能支持。

示意图如下:


光线追踪有一些很棒的特性,比如:能够生成高度真实感的图形,特别是对于表面光滑的对象,缺点是所需的计算量大的惊人.

原理其实非常的简单,但具体实现起来的时候会有很多细节的地方.


代码实现

向量类

可以表示空上的点（x,y,z）.

gvector3.h

#ifndef GVECTOR3_H #define GVECTOR3_H #include  #include  #define MIN(x,y) (x)>(y)?(y):(x); #define MAX(x,y) (x)>(y)?(x):(y); using namespace std;   class GVector3 {  public:     float x;     float y;     float z;      // 缺省构造函数     GVector3();     ~GVector3();      // 用户构造函数     GVector3(float posX, float posY, float posZ);     //输出向量信息     void getInfo();     //矢量加法     GVector3 operator+(GVector3 v);     //矢量减法     GVector3 operator-(GVector3 v);     //数乘     GVector3 operator*(float n);     //数除     GVector3 operator/(float n);     //向量点积     float dotMul(GVector3 v2);     //向量叉乘     GVector3 crossMul(GVector3 v2);     //绝对值化     GVector3 abs();     //获取分量中的最大值     float max();     //获取分量的最小值     float min();     //获取矢量长度     float getLength();     //向量单位化     GVector3 normalize();     //求两点之间的距离     float getDist(GVector3 v);     //返回零向量     static inline GVector3 zero(){ return GVector3(0,0,0); }     //打印向量的分量值     void show();  };  #endif // GVECTOR3_H

gvector3.cpp 

#include "gvector3.h"  GVector3::GVector3() { } GVector3::~GVector3() { } GVector3::GVector3(float posX, float posY, float posZ) {     x=posX;     y=posY;     z=posZ; }  GVector3 GVector3::operator+(GVector3 v) {     return GVector3(x+v.x,v.y+y,v.z+z); } GVector3 GVector3::operator-(GVector3 v) {     return GVector3(x-v.x,y-v.y,z-v.z); } GVector3 GVector3::operator*(float n) {     return GVector3(x*n,y*n,z*n); } GVector3 GVector3::operator/(float n) {     return GVector3(x/n,y/n,z/n); } void GVector3::getInfo() {     cout<<"x:"<

着重解释一下向量的点乘和叉乘。 

点乘，也叫向量的内积、数量积。顾名思义，求下来的结果是一个数。  在物理学中，已知力与位移求功，实际上就是求向量F与向量s的内积，即要用点乘。 
叉乘，也叫向量的外积、向量积。顾名思义，求下来的结果是一个向量，记这个向量为c。  向量c的方向与a,b所在的平面垂直，且方向要用“右手法则”判断（用右手的四指先表示向量a的方向，然后手指朝着手心的方向摆动到向量b的方向，大拇指所指的方向就是向量c的方向）。
在物理学中，已知力与力臂求力矩，就是向量的外积，即叉乘。 
数值上的计算，将向量用坐标表示（三维向量），  若向量a=(a1,b1,c1)，向量b=(a2,b2,c2)，  则  向量a·向量b=a1a2+b1b2+c1c2  向量a×向量b=  | i j k|  |a1 b1 c1|  |a2 b2 c2|  =(b1c2-b2c1,c1a2-a1c2,a1b2-a2b1)  （i、j、k分别为空间中相互垂直的三条坐标轴的单位向量）。
 
    
光线类
 
     
    
首先来看一下光线的表示方法。
 
    
 
    
 
    
当t=0时，p=e, 当t=1时，p=s.0 
    
这个结论在求交的时候会用到。
有两个私有成员，原点和方向，数学上可用参数函数来表示：r(t)=o+td;t>=0cray.h 
    
 
    
#ifndef CRAY_H #define CRAY_H #include  #include "gvector3.h" #define PI 3.14159 using namespace std; class CRay { 	private: 	GVector3 origin; 	GVector3 direction; 	public: 	CRay(); 	CRay(GVector3 o,GVector3 d); 	~CRay();     void setOrigin(GVector3 o); 	void setDirection(GVector3 d);     GVector3 getOrigin(); 	GVector3 getDirection(); 	//通过向射线的参数方程传入参数t而获得在射线上的点 	GVector3 getPoint(double t);  }; #endif 
 
    
cray.cpp 
    
 
    
#include "cray.h" CRay::CRay() { } CRay::~CRay() { } CRay::CRay(GVector3 o,GVector3 d) {     origin=o;     direction=d; } void CRay::setDirection(GVector3 d) {     direction=d; } void CRay::setOrigin(GVector3 o) {     origin=o; } GVector3 CRay::getDirection() {     return direction; } GVector3 CRay::getOrigin() {     return origin; } GVector3 CRay::getPoint(double t) {     return origin+direction*t; } 
 
    

 
    
初试画板
 
    这里用GLFW作为opengl的编程框架。
 GLFW是一个自由，开源，多平台的图形库，可用于创建窗口，渲染OpenGL，管理输入。
 GLFW的配置见《 GLFW入门学习》.这里主要要做的就是将我们窗口映射成像素的点阵，然后填充颜色。 
    
 
    
 
    
#include  #include  #include #define WINDOW_WIDTH  600 #define WINDOW_HEIGHT 600 void initScene(int w,int h) {     // 启用阴影平滑     glShadeModel( GL_SMOOTH );     // 黑色背景     glClearColor( 0.0, 0.0, 0.0, 0.0 );     // 设置深度缓存     glClearDepth( 1.0 );     // 启用深度测试     glEnable( GL_DEPTH_TEST );     // 所作深度测试的类型     glDepthFunc( GL_LEQUAL );     // 告诉系统对透视进行修正     glHint( GL_PERSPECTIVE_CORRECTION_HINT, GL_NICEST ); } //这里进行所有的绘图工作 void  drawScene() { float colorSpan=0.0005f;     float color=0.0f;     float pixelSize=2.0f;     float posY=-1.0f;     float posX=-1.0f;     long maxDepth=20;     glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);     glLoadIdentity();     //将原点移动到左下角     glTranslatef(-0.5f,-0.5f,-1.0f);     glPointSize(2.0);     glBegin(GL_POINTS);     double dx=1.0f/WINDOW_WIDTH;     double dy=1.0f/WINDOW_HEIGHT;     float dD=255.0f/maxDepth;     glBegin(GL_POINTS);      for (long y = 0; y < WINDOW_HEIGHT; ++y)     {         double sy = 1-dy*y;         for (long x = 0; x < WINDOW_WIDTH; ++x)         {             double sx =dx*x;             float colorR=x*1.0/WINDOW_WIDTH*255;             float colorB=y*1.0/WINDOW_HEIGHT*255;            glColor3ub(colorR,0,colorB);            glVertex2f(sx,sy);         }     }     // 交换缓冲区     glfwSwapBuffers(); } //重置窗口大小后的回调函数 void GLFWCALL resizeGL(int width, int height ) {     // 防止窗口大小变为0     if ( height == 0 )     {         height = 1;     }     // 重置当前的视口     glViewport( 0, 0, (GLint)width, (GLint)height );     // 选择投影矩阵     glMatrixMode( GL_PROJECTION );     // 重置投影矩阵     glLoadIdentity();     // 设置视口的大小     gluPerspective( 45.0, (GLfloat)width/(GLfloat)height, 0.1, 100.0 );     // 选择模型观察矩阵     glMatrixMode( GL_MODELVIEW );     glLoadIdentity(); }  int main( void ) {     //记录程序运行状态     int running = GL_TRUE;     //初始化 GLFW     if( !glfwInit() )     {         exit( EXIT_FAILURE );     }     // 创建一个OpenGL 窗口     if( !glfwOpenWindow( WINDOW_WIDTH,WINDOW_HEIGHT,6,6,6,0,32,0,GLFW_WINDOW) )     {         glfwTerminate();         exit( EXIT_FAILURE );     }     //初始化OpenGL窗口     initScene(WINDOW_WIDTH, WINDOW_HEIGHT);     //设置窗口大小发生变化时的回调函数     glfwSetWindowSizeCallback(resizeGL);     //主循环     while( running )     {         // OpenGL rendering goes here...         glClear( GL_COLOR_BUFFER_BIT );         // 当按下ESC键的时候触发         running = !glfwGetKey( GLFW_KEY_ESC ) &&glfwGetWindowParam( GLFW_OPENED ); 	drawScene();         //延时0.05秒 	glfwSleep(0.05 );     }     glfwTerminate();     //退出程序     exit( EXIT_SUCCESS ); } 
 
    
 渲染结果： 
    
 
    

 
    
 
    
球体
 
    
球面的几何定义是到空间某点距离一定的点的集合。
 
    
这里着重需要说明的是球体的isIntersected函数，用于求光线是否与球体相交，并将结果存在result中返回。
 中心点为c、半径为r的球体表面可用等式(equation)表示：||x-c||=r
 只要把x=r(t)带入，求解即可得交点。具体的运算过程如下（令v=o-c）。
 
    

 
    

 
    
若根号内为负数，即相交不发生。另外，由于这里只需要取最近的交点，因此正负号只需取负号。
 
    
而球体在交点的法向量可表示为n=（p - c），单位法向量为（p - c）/R
 
    
 
    所以空间球体可以用两个参数来表示：圆心位置和半径。
 代码如下。
 csphere.h
 
    
 
    
 
    
#ifndef CSPHERE_H #define CSPHERE_H #include "gvector3.h" #include "intersectresult.h" #include "cray.h" class CSphere {     public:         CSphere();         CSphere(GVector3 center,double radius);         CSphere(CSphere& s);         void setCenter(GVector3& c);         void setRadius(double r);         GVector3 getCenter();         double getRadius();         //获取物体表面一点的法线          virtual GVector3 getNormal(GVector3 point);         //用于判断射线和该物体的交点         virtual IntersectResult isIntersected(CRay RAY);         virtual ~CSphere();     protected:     private:         GVector3 center;         double radius; };  #endif // CSPHERE_H 
 
    
 csphere.cpp 
    
 
    
 
    
#include "csphere.h" #include "intersectresult.h" CSphere::CSphere() {     //ctor } CSphere::CSphere(GVector3 c,double r) {     center=c;     radius=r; } CSphere::CSphere(CSphere& s) {     center=s.getCenter();     radius=s.getRadius(); } CSphere::~CSphere() {     //dtor } void CSphere::setCenter(GVector3& c) {     center=c; } void CSphere::setRadius(double r) {     radius=r; } GVector3 CSphere::getCenter() {     return center; } double CSphere::getRadius() {     return radius; } GVector3 CSphere::getNormal(GVector3 p) {     return p-center; } IntersectResult CSphere::isIntersected(CRay _ray) {       IntersectResult result = IntersectResult::noHit();       GVector3 v = _ray.getOrigin() - center;         float a0 = v.dotMul(v) - radius*radius;         float DdotV = _ray.getDirection().dotMul(v);           if (DdotV <= 0) {             float discr = DdotV * DdotV - a0;             if (discr >= 0) {                 //                 result.isHit=1;                 result.distance=-DdotV - sqrt(discr);                 result.position=_ray.getPoint(result.distance);                 result.normal = result.position-center;                 result.normal.normalize();             }         } 		return result; } 
 
    
 
    

 
    还有一个结构体,用来表示体和光线相交的结果。 
    
 
    
#ifndef INTERSECTRESULT_H_INCLUDED #define INTERSECTRESULT_H_INCLUDED #include "gvector3.h" struct IntersectResult{     float distance;     bool isHit;     GVector3 position;     GVector3 normal;     static inline IntersectResult noHit() { return IntersectResult(); } };  #endif // INTERSECTRESULT_H_INCLUDED 
 
    
 
    

 
    
摄像机
 
    
摄影机在光线追踪系统里，负责把影像的取样位置，生成一束光线。
 由于影像的大小是可变的(多少像素宽x多少像素高)，为方便计算，这里设定一个统一的取样座标(sx, sy)，以左下角为(0,0)，右上角为(1 ,1)。
 从数学角度来说，摄影机透过投影(projection)，把三维空间投射到二维空间上。常见的投影有正投影(orthographic projection)、透视投影(perspective projection)等等。这里首先实现透视投影。
 
    
透视摄影机比较像肉眼和真实摄影机的原理，能表现远小近大的观察方式。透视投影从视点(view point/eye position)，向某个方向观察场景，观察的角度范围称为视野(field of view, FOV)。除了定义观察的向前(forward)是那个方向，还需要定义在影像平面中，何谓上下和左右。为简单起见，暂时不考虑宽高不同的影像，FOV同时代表水平和垂直方向的视野角度。
 
    

 
    
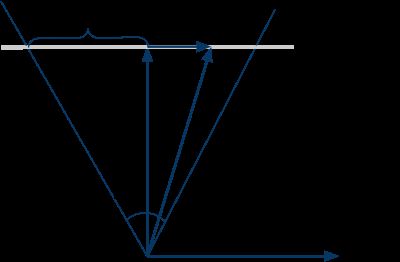
上图显示，从摄影机上方显示的几个参数。 forward和right分别是向前和向右的单位向量。
 因为视点是固定的，光线的起点不变。要生成光线，只须用取样座标(sx, sy)计算其方向d。留意FOV和s的关系为：tan(fov/2).
 把sx从[0, 1]映射到[-1,1]，就可以用right向量和s，来计算r向量。
 
    
代码实现：
 
    
perspectiveCamera.h
 
    
 
    
#ifndef PERSPECTIVECAMERA_H #define PERSPECTIVECAMERA_H #include "cray.h" class perspectiveCamera{     public:     perspectiveCamera();     ~perspectiveCamera();     perspectiveCamera(const GVector3& _eye,const GVector3& _front,const GVector3& _refUp,float _fov);     CRay generateRay(float x,float y);      private: 	GVector3 eye; 	GVector3 front; 	GVector3 refUp; 	float   fov; 	GVector3 right; 	GVector3 up; 	float   fovScale; }; #endif 
 
    
 perspectiveCamera.cpp 
    
 
    
 
    
#include"perspectiveCamera.h"  perspectiveCamera::perspectiveCamera() {  } perspectiveCamera::~perspectiveCamera() { } perspectiveCamera::perspectiveCamera(const GVector3& _eye,const GVector3& _front,const GVector3& _refUp,float _fov) {     eye=_eye;     front=_front;     refUp=_refUp;     fov=_fov;     right=front.crossMul(refUp);     up = right.crossMul(front);     fovScale = tan(fov* (PI  * 0.5f / 180)) * 2; } CRay perspectiveCamera::generateRay(float x,float y) {     GVector3 r = right*((x - 0.5f) * fovScale);     GVector3 u = up*((y - 0.5f) * fovScale);     GVector3 tmp=front+r+u;     tmp.normalize();     return CRay(eye,tmp); } 
 
    
 
    
 
    
 
    
渲染一个球
 
    
 
    
基本的工具类都准备好之后，我们就可以开始渲染一些东西，这里先把之前定义的球体渲染到窗口之中。
 
    
基本的做法是遍历影像的取样座标(sx, sy)，用Camera把(sx, sy)转为Ray3，和场景(例如Sphere)计算最近交点，把该交点的属性转为颜色，写入影像的相对位置里。
 
    
首先我们来渲染深度，深度(depth)就是从IntersectResult取得最近相交点的距离，因深度的范围是从零至无限，为了把它显示出来，可以把它的一个区间映射到灰阶。这里用[0, maxDepth]映射至[255, 0]，即深度0的像素为白色，深度达maxDepth的像素为黑色。
 
    
代码实现：
 
    
 
    
void renderDepth() {     glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);     glLoadIdentity();                                   // Reset The View     glTranslatef(-0.5f,-0.5f,-1.0f);     glPointSize(2.0);     float horiz=0.0;     float dep=10;     PerspectiveCamera camera( GVector3(horiz, 10, dep),GVector3(0, 0, -1),GVector3(0, 1, 0), 90);     long maxDepth=18;     CSphere* sphere1 = new CSphere(GVector3(0, 10, -10), 10.0);     float dx=1.0f/WINDOW_WIDTH;     float dy=1.0f/WINDOW_HEIGHT;     float dD=255.0f/maxDepth;     glBegin(GL_POINTS);     for (long y = 0; y < WINDOW_HEIGHT; ++y)     {         float sy = 1 - dy*y;         for (long x = 0; x < WINDOW_WIDTH; ++x)         {             float sx =dx*x;             CRay ray(camera.generateRay(sx, sy));             IntersectResult result = sphere1->isIntersected(ray);             if (result.isHit)             {                 double t=MIN(result.distance*dD,255.0f);                 int depth = (int)(255 -t);                 glColor3ub(depth,depth,depth);                 glVertex2f(sx,sy);             }          }     }      glEnd();     // 交换缓冲区     glfwSwapBuffers(); }
 
    
 渲染结果 
    
 
    

 
    

 
    
接下来我们来渲染一下交点法向量，法向量是一个单位向量，在计算交点的时候们就将其存储在result.normal中了，其每个元素的范围是[-1, 1]。把单位向量映射到颜色的常用方法为，把(x, y, z)映射至(r, g, b)，范围从[-1, 1]映射至[0, 255]。
 
    
代码实现：
 
    
 
    
void renderDepth() {     glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);     glLoadIdentity();                                   // Reset The View     glTranslatef(-0.5f,-0.5f,-1.0f);     glPointSize(2.0);     PerspectiveCamera camera( GVector3(0, 10, 10),GVector3(0, 0, -1),GVector3(0, 1, 0), 90);     long maxDepth=20;     CSphere* sphere1 = new CSphere(GVector3(0, 10, -10), 10.0);     camera.initialize();     float dx=1.0f/WINDOW_WIDTH;     float dy=1.0f/WINDOW_HEIGHT;     float dD=255.0f/maxDepth;     glBegin(GL_POINTS);     for (long y = 0; y < WINDOW_HEIGHT; ++y)     {         float sy = 1 - dy*y;         for (long x = 0; x < WINDOW_WIDTH; ++x)         {             float sx =dx*x;             CRay ray(camera.generateRay(sx, sy));             IntersectResult result = sphere1->isIntersected(ray);             if (result.isHit)             {                 //double t=MIN(result.distance*dD,255.0f);                 //int depth = (int)(255 -t);                 //xuanranshengdu                 //glColor3ub(depth,depth,depth);                 //xuanran normal                 glColor3ub(128*(result.normal.x+1),128*(result.normal.y+1),128*(result.normal.z+1));                 glVertex2f(sx,sy);             }         }     }     glEnd();     // 交换缓冲区     glfwSwapBuffers(); }
 
    
 渲染结果： 
    
 
    

 
    
球体上方的法向量是接近(0, 1, 0)，所以是浅绿色(0.5, 1, 0.5)。
 
    
 
    
结语
 
    
 
     入门篇就先到这里，通过一步步搭建我们的场景，对光线追踪有了一个基础的理解, 
    
 
    
 
     接下来我们会一步步深入一些高级的主题，比如材质，光照，雾... 
    
 
    
 
     
 参考： 
    
 
    
 
     用JavaScript玩转计算机图形学(一)光线追踪入门-http://www.cnblogs.com/miloyip/archive/2010/03/29/1698953.html
 光线追踪技术的理论和实践(面向对象)-http://blog.csdn.net/zhangci226/article/details/5664313 
    
 
    
 
     Wikipedia, Ray Tracing
 计算机图形学（第三版）（美）赫恩 著，（美）巴克 著。