三次作业分析
1:第一次作业
1.1:题目分析
第一次作业是简单多项式的求导。
多项式是由加法和减法运算符连接若干项组成。项分为变量项(带有系数的幂函数)和常数项(带符号整数)俩类
1.2:实现方案
首先,我建立PatternCheck类,帮我去掉空格和"\t",转化双符号即“++”,“--”等为对应的单运算符。
随后建立PolyCompute类,借助正则表达式帮我识别出对应的项类,
交给我建立的Item类形成对应的变量项。
PolyCompute对象的Deri(求导)任务交付给其通过Arrarylist容器管理的Item对象完成,
求导任务完成后,会得到一个记录求导后系数和指数字符串数组。
然后,就是很简单的思路,借助HashMap容器,以幂函数的指数为key,系数为value,完成本次任务的合并同类项。
对了,注意,提负系数的项放置首位,来进一步缩短输出。
程序UML图如下
1.3 结构分析
此次作业,我借助PatternCheck类来完成非法空白字符检查,清除多余的符号。然后借助PolyCompute类的构造函数来完成多项式的解析,最后借助PolyCompute类的Deri方法完成多项式求导,
最后借助PrintfAns方法完成求导后的答案输出。
本次作业度量如下
1.4 得失分析
本人第一次oo程序感到写的不是很好,还是有很多面对过程的影子存在。
强测稳如老狗,勉勉强强过了关,但是在互测环节,因为我程序的一个低级漏洞(强测居然没有测出来),被房间7个人集火攻击,最后被hack39次,(虽然都是同质bug)但还是让我十分不爽。
最后通过研讨课和查阅优秀同学代码学到了很多
1:异常捕捉(关键点一套,可以解决很多运行时异常问题,好吧!)
2:好的面对对象习惯-高聚合,低耦合
3:如何发现自己的bug
构建对应的输入树,尽可能全面测试自己的程序(当然,少不了评测数据覆盖攻击)
4:写出自己的思考流程图
强烈推荐,对于我这种菜狗,写一写思路流程图,就会发现自己在编写代码的过程中遗漏的要点
2:第二次作业
2.1:题目分析
本次作业是包含简单幂函数和简单正余弦函数的导函数求解
即对比第一次作业来言,1:新增因子类 sin(x) ,cos(x)。2:项的定义为因子类的乘积组合
2.2:实现方案
好吧,我的代码直接重构了,正好来整理下我的写法风格
首先,构建PolyCheck类,用来检查空格和"\t"存在的合法性,检查是否有其余空白字符,检查多符号的合法性。
注意,如果我想去除空格和多符号,我就要保证一点,就是去掉前后,我的问题性质没有发生变化。这是在我去除空格和多符号干扰前,必须要做的检查合法性操作的原因
然后,构建Poly(多项式)类,完成从经过Polycheck类预处理过的多项式,识别运算符“+”“-”,解析出项的任务
再然后,就是Item(项)类,借助“*”为分割符,通过正则表达式,来制造对应出因子
为了第三次作业的可扩展性,我设置了Factor类(父类),让SinFactor,CosFactor,XFactor都继承自它,并overload其Deri(求导)方法
虽然,这次,项组织存放因子的方法是三元组
合并化简方法,就是暴力搜索相同的三元组,让其系数相加,好吧(我没有overload hashcode方法,或者使用嵌套HashMap)
至于三角函数化简,我没有敢选择dfs+暴力搜索的方法,就是简单地暴力对比俩项,看是否可以提取出(sin(x)^2+cos(x)^2)
程序UML图如下
2.3 结构分析
此次作业借助PolyCheck类完成空白字符和多符号的检查和简化预处理
然后,借助表达式树来进行划分表达式类,项类,和因子类,逐层进行正则判断。
化简,则是在Poly类中通过比较项之间的关系来完成化简
本次作业度量如下
2.4 得失分析
因为我就仅仅进行较简单层次的化简,所以,强测还是十分顺利的通过
互测也可以说安稳地活了下来
但是,我的程序还是存在不合理的地方
首先,为了图一时方便,我没有把常数因子单独形成一个类,而是在Item类中,使用Biginteger存储系数,这个虽然在编程的时候,简化了我一部分的操作。但是在对象设计上是一种下下之选,不利于后面的扩展,此外,我这次作业采用的三元组形式来组织项所属因子关系,可扩展性极其不佳,导致我第三次作业,需要重新改写这一块。
3:第三次作业
3.1 题目分析
这次作业需要完成的任务依旧是包含简单幂函数和简单正余弦函数的导函数求解
但是,支持sin(),cos()的嵌套,新增表达式因子,这俩者组合就形成本次作业的罪恶源泉-嵌套组合规则
导致,本次作业在思路分析上提升了难度
3.2 实现方案
因为我第二次作业采用在项阶段通过三元组形式来存储项所对应的因子,而且parse出对应的指数
所以,我在第三次作业中重新改写了XFactor,SinFactor,CosFactor 三个类,而且为了完成嵌套组合规则,我让Poly(多项式)类也继承于Factor类
此外,考虑到求导操作时不应该对我原多项式因子造成影响,所以把传入参数全部变成不可变对象-String
parse(解析)思路如下
在多项式阶段,借助栈思想,区分出当前的运算加减符,并由此来分离出对应的项
在项阶段,同样借助于栈思想,区分出当前的乘法运算符,由此分离出因子,借助正则表达式的帮助完成因子的分类
为了完成嵌套规则,我把所有sin(),cos()因子括号中的字符串当作一个表达式因子,去除其可能包含的括号后,交给表达式因子类即Poly类进行解析
Deri(求导)思路如下
在因子阶段,完成对应的嵌套法则 即 sin(Factor)的导函数 -> cos(Factor)*Factor的导函数,把求导后的结果以字符串的形式返回给上一级,即Item
在项阶段,完成对应的乘法法则,我使用俩个Arraylist容器,第一个用来存储因子,后一个用来存储对应因子求导后的字符串,根据数学乘法求导法则
Factor1*Factor2*Factor3的导函数->Factor1的导函数*Factor2*Factor3+Factor1*Factor2的导函数*Factor3+........
用俩个for循环来模拟上述过程(我知道O(n^2)玩不起,但是我还是没想到什么比较好的模拟此过程的方法),最后还是以字符串的形式把求导结果返回上一级
在多项式阶段,完成对应的加减法规则,直接用“+”号拼接Item返回的求导结果即可
至于化简,由于本次化简难度过大,我没有尝试,只是打算在Item阶段,完成形式比较好的项求导结果的化简和替换隐式的(1*x^0)和(0*(****))为显式的1和0
本次作业UML图如下
3.3 结构分析
本次作业重构的地方仅仅只有三个因子类
其余类,如Poly类,Item类只需要overload一下toString()方法即可
至于,PolyCheck类简直是祖传代码,每次只需要改动一点点,就继续上岗使用
而且,我没有考虑化简,导致我第三次的代码编写工作量还小于第二次
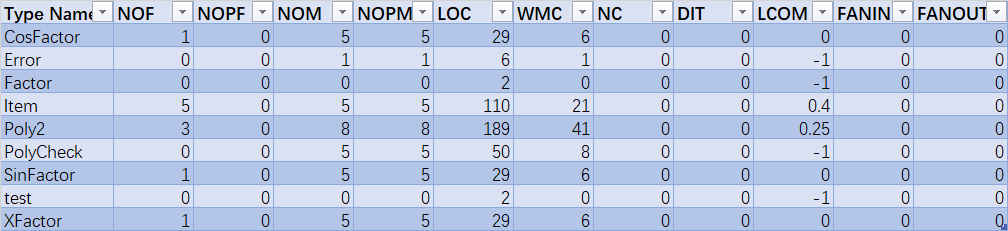
本次作业度量如下
3.4 得失分析
由于只要我不优化,就没有Bug的思想,我强测又一次苟活了下来,但是因为我编写XFactor类的时候,手抖,把10000打成了1000,导致互测被hack了一下
(我的评测机是假的评测机,连这个都发现不了)
还有一点令我不爽的是,我是隐式调用组合规则,而不是使用高大上的组合规则单独成控制类,这个导致我的可扩展性还是不佳
不过,我还是体验了一把可扩展性的好处,代码编写量真的少
4:单元分析
本单元大多还是在考验我们的问题分析能力和程序鲁棒性,对于算法优化方面,占比比较小
作业有很强的递进性,深刻地让我了解到了程序可扩展性的重要性
此外,通过研讨课和阅读其他人代码,让我收获很多,主要了解了一些好的面对对象思维,异常捕捉的使用,如何构造合适的输入树来测试自己程序,还有就是对象构造模式
本次作业特别适合工厂模式
总之,体验还是不错的,除了就是一个room中人太多,互测时间少,不能详细地读代码,就只能读个大概,就开始对拍模式