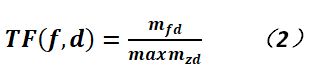前言
文本挖掘也是机器学习或者说是人工智能最需要处理的一类信息(其它的诸如语音、图像及视频处理等);随着数字信息化和网络化进程不断深入,用户的在线交流、发布、共享等都被以文字形式记录下来,它们成为分析语言和理解社会的重要素材来源,对于文本的挖掘主要包括文档分类、信息提取、文档聚类、主题建模等。
早期的文本处理主要偏向于依赖规则(依据语法规则生成相关语法树),但这类方法偏向静态,无法实时处理浩如烟海的互联网及其它来源的文字素材,更为重要的是它无法体现各种语言之间的相关性,而在上世纪80年×××始,机器学习方法被大量地运用到自然语言的处理上来(主要是基于统计学方法,被称为统计语言模型),实践表明这类方法比基于规则的方式更为可靠,而且更为适应各类变化。
文本挖掘事宜计算语言学、数理统计分析为理论基础,结合机器学习及信息检索技术,从文本素材中提取或发现相关知识,其所使用的手段不外乎文本切割、特征抽取、数据降维等。
本文所涉及的文本挖掘技术主要包含文本的向量空间模型(主要针对TFIDF算法,即Term Frequency-Inverse Document Frequency,词频-倒排文档频)、LDA(Latent Dirichlet Allocation潜在狄利克雷分配)以及Google的Word2Vec等通用方法。
文本向量空间模型
如何实现将文本数据结构化是文本挖掘的核心问题,这个问题又被称作文本的特征表示。向量空间模型是目前最为简便高效的文本表示模型之一,它的基本思想就是将单词从文档中提取出来,每个单词给予一定的权重;为了简化分析,一般不考虑单词在文档中的先后顺序(但单词不能重复),这时可以把这些单词所组成的东西看成是空间中的一个向量,而文档与文档之间的差异就可以使用余弦夹角的大小来判断。如果特征只有单词组成,而忽略其先后顺序,则这种方式被称作词袋模式(Bag of Words),而Word2Vec中的一种处理模式也是类似词袋模式,不过需要考虑单词在一定形式上的先后顺序。
而TFIDF就是一种常用的统计加权技术,它用来评估一个词对于一个文档的重要性以及这个词在一堆文档(文集)中的重要性;换言之,如果一个词在一个文档中出现的频次很高(这个就是所谓的TF,即词频),而且在文集中出现的频次较低(这个就是所谓的IDF,即反向文档频率),则可以认为这个词的识别度较高,可以用它来标识一个文档而区分其它的文档,形式化的,其计算公式如下:
在上式中,f就是文本集特征,的是文档,而TF(f,d)是词频,即特征词在文本中出现的频率,它的定义如下:
对于上式而言,mfd是f(特征词)在文档d中出现的次数,z是d中所有的特征词;对于倒排文档频而言,它就是度量特征词在文集中出现的频繁成都,用于降低那些在语料(Corpus)过于频繁出现的词的重要程度,主要是它们对于文档没有什么区分的能力,其计算公式如下:
LDA模型
传统的基于文本向量空间的模型,由于其维度太高(通常可能达到上万维),而且因为强调了权值,而忽略了术语之间的关系,从而导致所谓的“维度灾难”,故需将部分词的权值转化为更高层次的权值,这样可以弥补仅以词为特征的缺陷,这样在一定程度上也降低了维度;而所谓的主题(Topic)可以充当这一角色,它包含了若干个词。
Latent Dirichlet Allocation模型是一种典型的用于提取主题的概率潜语义模型,它是由Blei等人提出的,它是一种具有文本主题表示能力的非指导学习模型。
在LDA模型的符号系统中使用w来表示词,它是一个N维单位向量,我们依然使用d来表示文档,这两个概念和之前的基于向量空间模型没有太大区别,而使用z来表示主题,一个单词可以对应一个主题,一篇文档则由几个主题混合而成,记为{z1,z2,...,zN},它也是一个单位向量;文档语料(Corpus)集是M篇文档的集合,记为D={w1,w2,...,wM}。
LDA模型其建模过程就是一个文档的生成过程,生成模型是指模型可以随机生成一些可观测数据;LDA可以随机生成一篇由一个到多个主题组成的文档,其过程大致如下:
以一定概率在若干主题中选取主题;
以一定概率在选中的主题中抽取词语;
不断地重复上述步骤,直到生成一篇长度为N的文档。
如果以形式化的方式来表示,为如下公式所示:
在上式当中,就是根据参数获取主题的概率,而则是在一定主题之下获取词语的概率。那LDA模型和狄利克雷分布究竟有什么关系?或者说这个模型为什么要使用狄利克雷来命名?其原因在于Blei等人研究发现如果生成多篇文档,则主题的分布也应该遵照一定的经验概率模型,在这个模型中就是狄利克雷分布;我们知道狄利克雷分布被称作分布的分布,就是可以用它来生成其它分布(其实主要是多项分布)的参数,故从这个角度而言,公式4可以写为如下形式(参数的分布为Dir()):
故综上所述,LDA模型的基本思想就是将每个文档表示为潜在主题的随机混合模型,而每个主题标识为一系列词语的概率分布。
具体到生成一篇文档而言,其步骤如下:
从泊松分布中随机抽取N(文档的长度);
选取从狄利克雷分布中生成参数,它是一个k维随机向量(回忆下狄利克雷分布的形式即可知),它表示文档中k个主题发生之概率,k固定为已知量;
对于生成文档中每一个词语而言,先根据多项式分布(参数已由上步生成)选取主题,然后在给定主题下选择词语,其概率为,其中为在给定主题下的多项分布,参数是一个k*N的矩阵,,它代表主题i下生成单词j的概率。
故LDA模型的联合概率如以下公式所示:
使用LDA模型对文本建模,就是要估计参数和,前者反映了主题模型的性质,而后者则反映了词语在给定主题下的性质,但其实利用极大似然法是很难求解这两个参数的,可以在EM算法(这个算法也是所谓机器学习的“十大算法”,其主要思想是在无法对目标函数直接求导数时,转而利用Jenson不等式,求其下界函数的导数,然后不断抬高下界而达到逼近目标函数的作用)中结合变分推断来估计它们。
Word2Vec方法
从这个方法的名称来看就可知它主要的目的是将词转换为向量,这个和文本向量空间模型是完全不同的,因为后者是将文章中的多个词转化为向量,这里需要注意差别。将词转化为向量有个最为普通的方法,即令有长度为m的字典(这里注意字典和语料的区别,语料是可以包含有重复单词的),其对应词的维度值为1,而其它维度的值只能为0,即这个向量就是所谓的One-hot向量,显然这种方法会造成数据的过于稀疏,而且各个词向量之间没有任何关系,它们之间是正交的,即,故这种表示方法虽然简单,但实际上没有什么太大的价值。
而Google的Word2Vec方法另辟蹊径,利用单词在上下文中的关系,对其进行向量化而取得了非常不错的效果,甚至在自然语言互译中也有很大作用(因为类似的单词在向量空间上的距离较近),在介绍这个方法的文章中,《Word2Vec中的数学原理详解》是非常不错的一篇博文,值得仔细研读,但其中对于为什么要使用Hierarchical Softmax(层级式的Softmax)作为网络的输出其实并没有特别地进行说明,这造成在读这篇文章之初以为是必须要使用这种方法(一开始笔者也是这么认为的),有的网友认为是基于缩减计算量的需要,我也认为确实如此,但相关文章中也没有提到其根本原因,故在这篇文章中进行一定的说明,其实也可以不用基于层级的Softmax方法作为最终输出,但这可以让我们认识到,对于一个具有海量输出的神经网络而言,使用层级式的Softmax效果要优于一般的Softmax,这个对于手写汉字的识别或人脸识别可能也是如此,因为汉字的输出不会就那么若干个字母及数字。
本文无意于过多讨论和描述Word2Vec的原理,因为相关文档已经描述的极为清楚了,但考虑到完整性,还是会引用一些《Word2Vec中的数学原理详解》内容;另外,文章最后一节讲述到了这个方法的一些实现细节,其中有关于算法加速部分,这个倒是可以为广大程序员所参考,但在谈到对于指数函数求值的部分时,文章指出考虑到算法实现速度,会将指数函数使用泰勒公式展开,并且采用查表法获取相应的值,笔者在这里表示不太认同这种做法(不知原算法实现人员是基于什么平台开发的),因为笔者也在早期的实践中也使用这种方式来求取指数函数的函数值,但发现其实和直接使用libm中的数学库没有存在什么速度上的明显差异(基于CPU时钟数进行衡量),这里的原因主要有两点,其一是数学库中已经使用了相关优化方法,其二是计算的速度不仅取决于算法的优化,主要还有Cache的命中情况(对于早期的CPU,程序员可能需要显式地对数据进行预取,即利用prefetch指令,而新一代的处理器在这方面做得已经足够智能了)。
Word2Vec主要包含两个主要方法,其一是所谓的CBOW模型,而其二则是所谓的Skip-gram模型,它们之间存在一种互补的关系,另外还有一种基于负采样的训练。
前文提到Word2Vec并非采用传统的Softmax作为输出,而是使用Hierarchical Softmax,其主要表现形式就是哈夫曼数(Huffman Tree),这种数主要用于编码上,主要特点是首先它是一个二叉树(当然不是一般意义的二叉搜索树、排序树或平衡树,如AVL或红黑树等常见二叉树;这种树是数据结构中较为基础的一种,可以参看相关教科书),其次频率越高的单词其结点所在位置越靠近树根,而其所谓的编码就长度越短,从而可以从下面的相关推导可以看出,计算量越小,这就是为什么要采用这种有些奇怪的输出结构的原因,但总体还是保持了归一化的特性;而这颗异常庞大(因为单词很多)的哈夫曼树的叶子节点都是单词,非叶子节点包含了需要求解的参数向量,对于这些参数向量以及单词向量的最大化的目标函数就是求解的根本目的。考虑到方便起见,默认树的左子树编码为0,右子树编码为1,至于是否则需要去除单词中的所谓Stop Words(比如中文的“的”,英文的“of”等频率很高,但又没有实际意义的词),那就可能需要根据实际情况来处理。
CBOW
现令单词的向量(使用x表示之)和参数(使用θ表示之)向量都是m维的实向量,则,假定对于某个单词w,其前后各考察c(c一般可能不宜过大)个单词,则共有2c个单词,则对于每一次单独训练(当然其上下文不会只有2c个单词,故针对每一次而言,只取一种上下文场景)而言,需将这些单词的向量进行累加(就是简单的向量加法;在训练最初始,可以随机生成这些单词向量),生成一个向量,它被记作Xw;在其中还会使用Sigmoid函数来计算相关概率,那么对于CBOW模型而言,其目标函数就是:
对于上式而言,在实际操作中,就是把词向量和的变化率累加,再平均分摊到每个词向量上,其中w'是w的上下文。
Skip-gram
以上是对于CBOW(根据中间单词求上下文单词向量)模式的相关公式推导,而对于Skip-gram(根据上下文求中间单词向量)模式而言,其实比较类似,其目标函数如下:
可以看出其形式与公式7较为类似,所不同的就是中间多了一层对于单词w上下文的求和(这个很好理解,因为这是多个单词求一个单词的向量),另外就是Sigmoid函数的参数略有不同而已(其实还是一样)。
那么有了目标函数,则也能得到最终的参数更新公式(这个中间的步骤就不再重复了,读者可以参考相关文档,或者自行推导,其过程并不繁复),如下:
负采样
以上就是对于两个主要模型的相关比较简略的推导,而负采样又是什么呢?因为在分类模型中,据研究表明如果给出了正例,而且还给出负例则能提高模型的识别度,故在Word2Vec中也实现了所谓的负采样,在CBOW的负采样中即最大化如下目标函数:
NEG(w)就是w的负例集合,我们希望对于正例而言则概率越大越好,而负例则越小越好,于是目标函数就是:
对于Skip-gram的负采样,十分类似,不再赘述,可参考相关文档。
其它
最后简单地讨论下如果输出层不使用Hierarchical Softmax,而用一般的Softmax,则计算量为什么会非常巨大。假定网络输入采用m个神经元(当然也可以使用2c*m个神经元,即不将输入向量相加,但处理起来稍有些麻烦),也不使用隐层(显然也可以使用,但计算量又更是巨大,而且效果不彰),输出神经元就是语料集合的大小,它们之间没有层次的关系,输入和输出之间为全连接,这时就可以将需要优化的参数θ看作是神经元之间连接的权重,网络中共有m*|C|条连接,则相关目标函数就转变成如下形式(红色部分是为了区分w的含义不同):
显然,对于上式而言,由于Softmax公式的需要,必须基于全局的计算概率(相对而言,采用层次式的Softmax就不需要每次都遍历全局,这里就是巧妙处之所在,唯一需要付出的可能就是左右子树的指针开销,但若能采用整型索引进行存储,可以减少一定的内存使用),而且因为这些参数在迭代的过程中会产生不停地变化,无法复用,所以计算量十分巨大。