如何在Python中用scikit-learn生成测试数据集
在本教程中,你将学习测试问题及如何在 Python 中使用 scikit-learn 进行测试。
完成本教程后,你将知道:
-
如何生成多类分类预测测试问题
-
如何生成二进制分类预测测试问题
-
如何生成线性回归预测测试问题
让我们开始吧。
教程概述
本教程被分成了 3 个部分,他们分别是:
1. 测试数据集
2. 分类测试问题
3. 回归测试问题
测试数据集
开发和实现机器学习算法时的一个问题是如何知道你是否已经正确实现了他们——它们似乎在有 bug 时也能工作。
测试数据集是小型设计问题,它能让你测试、调试算法和测试工具。它们对于更好地理解算法响应超参数变化的行为方面也很有用。
下面是测试数据集的一些理想特性:
-
它们可以快速、容易地生成。
-
它们包含「已知」或「理解」的结果来和预测进行比较。
-
它们是随机的,每次生成时都允许在同一个问题上随机变化。
-
它们很小、容易在而二维中实现可视化。
-
它们可以被增大。
我建议在开始一个新的机器学习算法或开发一个新的测试工具时使用测试数据集。scikit-learn 是一个用于机器学习的 Python 库,它提供了生成一组测试问题的函数。
在本教程中,我们将看一些为分类和回归算法生成测试问题的例子。
分类测试问题
分类是将标签分配给数据的问题。在本节中,我们将看三个分类问题:blobs、moons 和 circles。
Blobs 分类问题
make_blobs() 函数可被用于生成具有高斯分布的 blobs 点。你可以控制生成 blobs 的数量,生成样本的数量以及一系列其他属性。考虑到 blobs 的线性可分性质,该问题也适用于线性分类问题。
下面的例子是一个多类分类预测问题,它生成了一个具有三个 blobs 的 2D 样本数据集。每个数据有两个输入和 0、1 或 2 个类的值。
-
# generate 2d classification dataset -
X, y = make_blobs(n_samples=100, centers=3, n_features=2)
完整的例子如下所示。
-
from sklearn.datasets.samples_generator import make_blobs -
from matplotlib import pyplot -
from pandas import DataFrame -
# generate 2d classification dataset -
X, y = make_blobs(n_samples=100, centers=3, n_features=2) -
# scatter plot, dots colored by class value -
df = DataFrame(dict(x=X[:,0], y=X[:,1], label=y)) -
colors = {0:'red', 1:'blue', 2:'green'} -
fig, ax = pyplot.subplots() -
grouped = df.groupby('label') -
for key, group in grouped: -
group.plot(ax=ax, kind='scatter', x='x', y='y', label=key, color=colors[key]) -
pyplot.show()
运行该示例将生成该问题的输入和输出,然后创建一个方便的 2D 图,用不同的颜色显示不同类的点。注意,考虑到问题生成器的随机特性,你的特定数据集和结果图会有所不同。这是一个特点,而不是一个错误。
Blobs 测试分类问题的散点图
我们将会在下面的例子中使用相同的示例结构。
Moons 分类问题
make_moons() 函数用于二进制分类并且将生成一个漩涡模式,或者两个 moons。你可以控制 moon 形状中的噪声量,以及要生产的样本数量。
这个测试问题适用于能够学习非线性类边界的算法。下面的例子生成了一个中等噪音的 moon 数据集。
-
# generate 2d classification dataset -
X, y = make_moons(n_samples=100, noise=0.1)
完整的例子如下所示。
-
from sklearn.datasets import make_moons -
from matplotlib import pyplot -
from pandas import DataFrame -
# generate 2d classification dataset -
X, y = make_moons(n_samples=100, noise=0.1) -
# scatter plot, dots colored by class value -
df = DataFrame(dict(x=X[:,0], y=X[:,1], label=y)) -
colors = {0:'red', 1:'blue'} -
fig, ax = pyplot.subplots() -
grouped = df.groupby('label') -
for key, group in grouped: -
group.plot(ax=ax, kind='scatter', x='x', y='y', label=key, color=colors[key]) -
pyplot.show()
运行该示例会生成并绘制数据集以供查阅,然后再按照指定的类对样本着色。
Moons 测试分类问题的散点图
Circles 分类问题
make_circles() 函数生成一个数据集落入同心圆的二进制分类问题。再一次地,与 moons 测试问题一样,你可以控制形状中的噪声量。该测试问题适用于可以学习复杂的非线性流行的算法。下面的例子中生成了一个具有一定噪音的 circles 数据集。
-
# generate 2d classification dataset -
X, y = make_circles(n_samples=100, noise=0.05)
完整例子如下所示。
-
from sklearn.datasets import make_circles -
from matplotlib import pyplot -
from pandas import DataFrame -
# generate 2d classification dataset -
X, y = make_circles(n_samples=100, noise=0.05) -
# scatter plot, dots colored by class value -
df = DataFrame(dict(x=X[:,0], y=X[:,1], label=y)) -
colors = {0:'red', 1:'blue'} -
fig, ax = pyplot.subplots() -
grouped = df.groupby('label') -
for key, group in grouped: -
group.plot(ax=ax, kind='scatter', x='x', y='y', label=key, color=colors[key]) -
pyplot.show()
运行该示例并绘制数据集以供查阅。
Circles 测试分类问题的散点图
回归测试问题
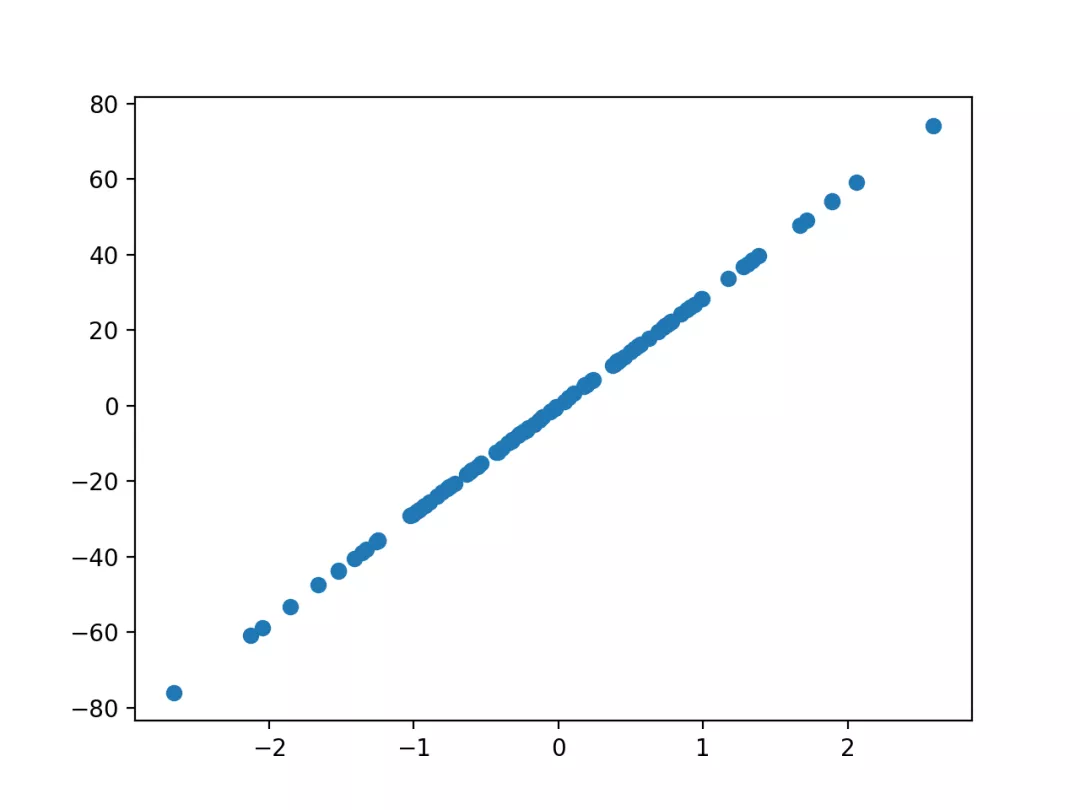
回归是根据观察数据预测数量的问题。make_regression() 函数将创建一个输入和输出具有线性关系的数据集。你可以配置样本数量,输入特征数量,噪声级别等等。该数据集适用于可以学习线性回归函数的算法。
下面的例子将生成 100 个示例,他们具有适度的噪声,都有一个输入特征和一个输出特征。
-
# generate regression dataset -
X, y = make_regression(n_samples=100, n_features=1, noise=0.1)
完整例子如下所示。
-
from sklearn.datasets import make_regression -
from matplotlib import pyplot -
# generate regression dataset -
X, y = make_regression(n_samples=100, n_features=1, noise=0.1) -
# plot regression dataset -
pyplot.scatter(X,y) -
pyplot.show()
运行该示例将生成数据并绘制 x 和 y 的关系,考虑到它是线性的,所以结果是很简单的。
扩展
本节列出了一些你可能想要探讨的扩展该教程的想法。
-
比较算法。选择一个测试问题,并比较该问题的一系列算法并汇报性能。
-
放大问题。选择一个测试问题并探索将其放大,用级数法来可视化结果,也可以探索一个特定算法模型技能和问题规模。
-
其他问题。库提供了一套其他测试问题;为每个问题编写了一个代码示例来展示它们是如何工作的。
拓展阅读
如果你想要更深入的了解,本节提供了关于该课题更多的资源。
-
scikit-learn 用户指南: Dataset loading utilities (http://scikit-learn.org/stable/datasets/index.html)
-
scikit-learn API: sklearn.datasets: Datasets (http://scikit-learn.org/stable/modules/classes.html#module-sklearn.datasets)
总结
在本教程中,我们学习了测试问题及如何用 scikit-learn 在 Python 中使用他们。
具体来说,其中包括:
-
如何生成多类分类预测测试问题;
-
如何生成二进制分类预测测试问题;
-
如何生成线性回归预测测试问题。