Leetcode 5410:课程安排IV
题目描述
你总共需要上 n 门课,课程编号依次为 0 到 n-1 。
有的课会有直接的先修课程,比如如果想上课程 0 ,你必须先上课程 1 ,那么会以 [1,0] 数对的形式给出先修课程数对。
给你课程总数 n 和一个直接先修课程数对列表 prerequisite 和一个查询对列表 queries 。
对于每个查询对 queries[i] ,请判断 queries[i][0] 是否是 queries[i][1] 的先修课程。
请返回一个布尔值列表,列表中每个元素依次分别对应 queries 每个查询对的判断结果。
注意:如果课程 a 是课程 b 的先修课程且课程 b 是课程 c 的先修课程,那么课程 a 也是课程 c 的先修课程。
示例 1:
输入:n = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]] 输出:[false,true] 解释:课程 0 不是课程 1 的先修课程,但课程 1 是课程 0 的先修课程。
示例 2:
输入:n = 2, prerequisites = [], queries = [[1,0],[0,1]] 输出:[false,false] 解释:没有先修课程对,所以每门课程之间是独立的。
示例 3:
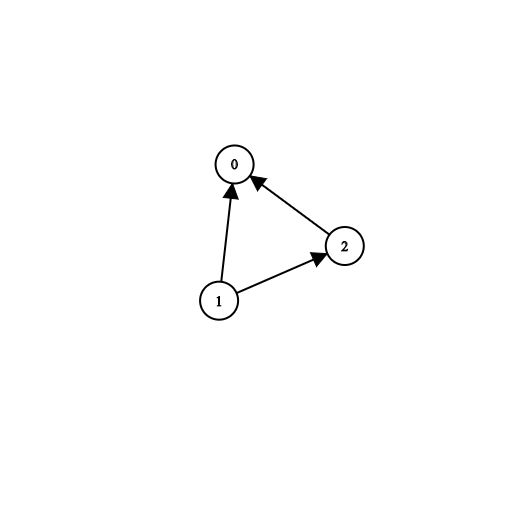
输入:n = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]] 输出:[true,true]
示例 4:
输入:n = 3, prerequisites = [[1,0],[2,0]], queries = [[0,1],[2,0]] 输出:[false,true]
示例 5:
输入:n = 5, prerequisites = [[0,1],[1,2],[2,3],[3,4]], queries = [[0,4],[4,0],[1,3],[3,0]] 输出:[true,false,true,false]
提示:
2 <= n <= 1000 <= prerequisite.length <= (n * (n - 1) / 2)0 <= prerequisite[i][0], prerequisite[i][1] < nprerequisite[i][0] != prerequisite[i][1]- 先修课程图中没有环。
- 先修课程图中没有重复的边。
1 <= queries.length <= 10^4queries[i][0] != queries[i][1]
解题思路
class Solution {
public:
bool dfs(vector> &graph, int pre, int post, vector &vis){
if(pre == post) return true;
vis[pre] = 1;
for(int i=0; i checkIfPrerequisite(int n, vector>& prerequisites, vector>& queries) {
vector ans;
vector> graph(n);
for(auto &it : prerequisites){
graph[it[0]].push_back(it[1]);
}
for(auto &it : queries){
vector vis(n);
ans.push_back(dfs(graph, it[0], it[1], vis));
}
return ans;
}
};