相关系数矩阵与heatmap热力图
在学习机器学习的过程中,我们需要观察特征之间的相似性。这时候python提供的seaborn.heatmap函数就可以帮助我们来查看特征之间的相似性。
1.官方API介绍
首先我们看一下 官方提供的heatmap官方API:
我们依次来介筛下这些参数:
- data(数据参数):矩阵数据集,可以是numpy的数组(array),也可以是pandas的DataFrame。如果是DataFrame,则df的index/column信息会分别对应到heatmap的columns和rows,即df.index是热力图的行标,df.columns是热力图的列标。
- vamx,vmin(矩阵块颜色参数):分别是热力图的颜色取值最大和最小范围,默认是根据data数据表里的取值确定
- .cmap:从数字到色彩空间的映射,取值是matplotlib包里的colormap名称或颜色对象,或者表示颜色的列表;改参数默认值:根据center参数设定.
- center:数据表取值有差异时,设置热力图的色彩中心对齐值;通过设置center值,可以调整生成的图像颜色的整体深浅;设置center数据时,如果有数据溢出,则手动设置的vmax、vmin会自动改变.
- robust:默认取值False;如果是False,且没设定vmin和vmax的值,热力图的颜色映射范围根据具有鲁棒性的分位数设定,而不是用极值设定.
- annot(annotate的缩写):默认取值False;如果是True,在热力图每个方格写入数据;如果是矩阵,在热力图每个方格写入该矩阵对应位置数据
- fmt:字符串格式代码,矩阵上标识数字的数据格式,比如保留小数点后几位数字
- annot_kws:默认取值False;如果是True,设置热力图矩阵上数字的大小颜色字体,matplotlib包text类下的字体设置:
- linewidths:定义热力图里“表示两两特征关系的矩阵小块”之间的间隔大小
- linecolor:切分热力图上每个矩阵小块的线的颜色,默认值是’white’
- cbar:是否在热力图侧边绘制颜色刻度条,默认值是True
- cbar_kws:热力图侧边绘制颜色刻度条时,相关字体设置,默认值是None
- cbar_ax:热力图侧边绘制颜色刻度条时,刻度条位置设置,默认值是None
- xticklabels, yticklabels:xticklabels控制每列标签名的输出;yticklabels控制每行标签名的输出。默认值是auto。如果是True,则以DataFrame的列名作为标签名。如果是False,则不添加行标签名。如果是列表,则标签名改为列表中给的内容。如果是整数K,则在图上每隔K个标签进行一次标注。 如果是auto,则自动选择标签的标注间距,将标签名不重叠的部分(或全部)输出
- mask:控制某个矩阵块是否显示出来。默认值是None。如果是布尔型的DataFrame,则将DataFrame里True的位置用白色覆盖掉
- ax:设置作图的坐标轴,一般画多个子图时需要修改不同的子图的该值
- **kwargs:All other keyword arguments are passed to ax.pcolormesh
2.代码展示
2.1 构造数据表
import seaborn as sns
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
region = ['Azerbaijan','Bahamas', 'Bangladesh', 'Belize', 'Bhutan',
'Cambodia', 'Cameroon', 'Cape Verde', 'Chile', 'China'] #10个
kind = ['Afforestation & reforestation', 'Biofuels', 'Biogas', 'Biomass', 'Cement'] #5个
np.random.seed(20180316)
arr_region = np.random.choice(region, size=(200,))
list_region = list(arr_region)
arr_kind = np.random.choice(kind, size=(200,))
list_kind = list(arr_kind)
values = np.random.randint(100, 200, 200)
list_values = list(values)
df = pd.DataFrame({'region':list_region,'kind': list_kind,'values':list_values})
df.head(10)

2.2 将DataFrame数据表转化成"数据透视表"
import pandas as pd
pt = df.pivot_table(index='kind', columns='region', values='values', aggfunc=np.sum)
#数据透视表pt
#index是行,columns是列,values是表中展示的数据,aggfunc是表中展示每组数据使用的运算

2.3 热力图矩阵块颜色参数
利用参数cmap改变颜色。
#cmap(颜色)
import matplotlib.pyplot as plt
f, (ax1,ax2) = plt.subplots(figsize = (6,4),nrows=2)
# cmap用cubehelix map颜色
cmap = sns.cubehelix_palette(start = 1.5, rot = 3, gamma=0.8, as_cmap = True)
sns.heatmap(pt, linewidths = 0.05, ax = ax1, vmax=900, vmin=0, cmap=cmap)
ax1.set_title('cubehelix map')
ax1.set_xlabel('')
ax1.set_xticklabels([]) #设置x轴图例为空值
ax1.set_ylabel('kind')
# cmap用matplotlib colormap
sns.heatmap(pt, linewidths = 0.05, ax = ax2, vmax=900, vmin=0, cmap='rainbow')
# rainbow为 matplotlib 的colormap名称
ax2.set_title('matplotlib colormap')
ax2.set_xlabel('region')
ax2.set_ylabel('kind')

利用参数center改变颜色
#center的用法(颜色)
f, (ax1,ax2) = plt.subplots(figsize = (6, 4),nrows=2)
cmap = sns.cubehelix_palette(start = 1.5, rot = 3, gamma=0.8, as_cmap = True)
sns.heatmap(pt, linewidths = 0.05, ax = ax1, cmap=cmap, center=None )
ax1.set_title('center=None')
ax1.set_xlabel('')
ax1.set_xticklabels([]) #设置x轴图例为空值
ax1.set_ylabel('kind')
# 当center设置小于数据的均值时,生成的图片颜色要向0值代表的颜色一段偏移
sns.heatmap(pt, linewidths = 0.05, ax = ax2, cmap=cmap, center=200)
ax2.set_title('center=3000')
ax2.set_xlabel('region')
ax2.set_ylabel('kind')

利用参数robust改变颜色
#robust的用法(颜色)
f, (ax1,ax2) = plt.subplots(figsize = (6,4),nrows=2)
cmap = sns.cubehelix_palette(start = 1.5, rot = 3, gamma=0.8, as_cmap = True)
sns.heatmap(pt, linewidths = 0.05, ax = ax1, cmap=cmap, center=None, robust=False )
ax1.set_title('robust=False')
ax1.set_xlabel('')
ax1.set_xticklabels([]) #设置x轴图例为空值
ax1.set_ylabel('kind')
sns.heatmap(pt, linewidths = 0.05, ax = ax2, cmap=cmap, center=None, robust=True )
ax2.set_title('robust=True')
ax2.set_xlabel('region')
ax2.set_ylabel('kind')

2.4 热力图矩阵块注释参数
#annot(矩阵上数字),annot_kws(矩阵上数字的大小颜色字体)matplotlib包text类下的字体设置
import numpy as np
np.random.seed(20180316)
x = np.random.randn(4, 4)
print(x)
f, (ax1, ax2) = plt.subplots(figsize=(6,6),nrows=2)
sns.heatmap(x, annot=True, ax=ax1)
sns.heatmap(x, annot=True, ax=ax2, annot_kws={'size':9,'weight':'bold', 'color':'blue'})
# Keyword arguments for ax.text when annot is True. http://stackoverflow.com/questions/35024475/seaborn-heatmap-key-words
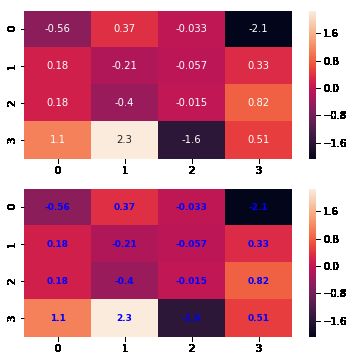
#fmt(字符串格式代码,矩阵上标识数字的数据格式,比如保留小数点后几位数字)
import numpy as np
np.random.seed(0)
x = np.random.randn(4,4)
f, (ax1, ax2) = plt.subplots(figsize=(6,6),nrows=2)
sns.heatmap(x, annot=True, ax=ax1)
sns.heatmap(x, annot=True, fmt='.1f', ax=ax2)

2.5 热力图矩阵块之间间隔线参数
#linewidths(矩阵小块的间隔),linecolor(切分热力图矩阵小块的线的颜色)
import matplotlib.pyplot as plt
f, ax = plt.subplots(figsize = (6,4))
cmap = sns.cubehelix_palette(start = 1, rot = 3, gamma=0.8, as_cmap = True)
sns.heatmap(pt, cmap = cmap, linewidths = 0.05, linecolor= 'red', ax = ax)
ax.set_title('Amounts per kind and region')
ax.set_xlabel('region')
ax.set_ylabel('kind')

#xticklabels,yticklabels横轴和纵轴的标签名输出
import matplotlib.pyplot as plt
f, (ax1,ax2) = plt.subplots(figsize = (5,5),nrows=2)
cmap = sns.cubehelix_palette(start = 1.5, rot = 3, gamma=0.8, as_cmap = True)
p1 = sns.heatmap(pt, ax=ax1, cmap=cmap, center=None, xticklabels=False)
ax1.set_title('xticklabels=None',fontsize=8)
p2 = sns.heatmap(pt, ax=ax2, cmap=cmap, center=None, xticklabels=2, yticklabels=list(range(5)))
ax2.set_title('xticklabels=2, yticklabels is a list',fontsize=8)
ax2.set_xlabel('region')

#mask对某些矩阵块的显示进行覆盖
f, (ax1,ax2) = plt.subplots(figsize = (5,5),nrows=2)
cmap = sns.cubehelix_palette(start = 1.5, rot = 3, gamma=0.8, as_cmap = True)
p1 = sns.heatmap(pt, ax=ax1, cmap=cmap, xticklabels=False, mask=None)
ax1.set_title('mask=None')
ax1.set_ylabel('kind')
p2 = sns.heatmap(pt, ax=ax2, cmap=cmap, xticklabels=True, mask=(pt<800))
#mask对pt进行布尔型转化,结果为True的位置用白色覆盖
ax2.set_title('mask: boolean DataFrame')
ax2.set_xlabel('region')
ax2.set_ylabel('kind')

2.6 用mask实现:凸显某些数据
f,(ax1,ax2) = plt.subplots(figsize=(4,6),nrows=2)
x = np.array([[1,2,3],[2,0,1],[-1,-2,0]])
sns.heatmap(x, annot=True, ax=ax1)
sns.heatmap(x, mask=x < 1, ax=ax2, annot=True, annot_kws={"weight": "bold"}) #把小于1的区域覆盖掉

3 相关系数矩阵
通常,样本是由多维特征的构成的,把每个特征维度都看成一个随机变量,为了考查两两特征间的关系,可以借助随机变量的协方差。
协方差是对两个随机变量联合分布线性相关程度的一种度量。
cov ( X i , X j ) = E [ ( X i − E ( X i ) ) ( X j − E ( X j ) ) ] var ( X i ) = E [ ( X i − E ( X i ) ) 2 ] var ( X j ) = E [ ( X j − E ( X j ) ) 2 ] \begin{array}{c}{\operatorname{cov}\left(X_{i}, X_{j}\right)=E\left[\left(X_{i}-E\left(X_{i}\right)\right)\left(X_{j}-E\left(X_{j}\right)\right)\right]} \\ {\operatorname{var}\left(X_{i}\right)=E\left[\left(X_{i}-E\left(X_{i}\right)\right)^{2}\right]} \\ {\operatorname{var}\left(X_{j}\right)=E\left[\left(X_{j}-E\left(X_{j}\right)\right)^{2}\right]}\end{array} cov(Xi,Xj)=E[(Xi−E(Xi))(Xj−E(Xj))]var(Xi)=E[(Xi−E(Xi))2]var(Xj)=E[(Xj−E(Xj))2]
由于随机变量的取值范围不同,没有可比性,对其进行归一化处理,得到相关系数
η = cov ( X i , X j ) var ( X i ) ⋅ var ( X j ) \eta=\frac{\operatorname{cov}\left(X_{i}, X_{j}\right)}{\sqrt{\operatorname{var}\left(X_{i}\right) \cdot \operatorname{var}\left(X_{j}\right)}} η=var(Xi)⋅var(Xj)cov(Xi,Xj)
其中,|η|≤1:
- 1表示随机变量Xi和Xj完全线性正相关;
- −1表示随机变量Xi和Xj完全线性负相关;
- 0表示随机变量Xi和Xj线性无关,但是线性无关并不代表完全无关。
样本(共m个)随机变量 X = [ X 1 , X 2 , ⋯ , X n ] T X=\left[X_{1}, X_{2}, \cdots, X_{n}\right]^{T} X=[X1,X2,⋯,Xn]T,第K个样本为 { x k . = [ x k 1 , x k 2 , ⋯ , x k n ] T ∣ 1 ≤ k ≤ m } \left\{x_{k .}=\left[x_{k 1}, x_{k 2}, \cdots, x_{k n}\right]^{T} | 1 \leq k \leq m\right\} {xk.=[xk1,xk2,⋯,xkn]T∣1≤k≤m}.则任意两个维度特征的协方差为
cov ( X i , X j ) = ∑ k = 1 m ( x k i − x . i ‾ ) ( x k j − x . j ‾ ) m − 1 \operatorname{cov}\left(X_{i}, X_{j}\right)=\frac{\sum_{k=1}^{m}\left(x_{k i}-\overline{x_{ . i}}\right)\left(x_{k j}-\overline{x_{ . j}}\right)}{m-1} cov(Xi,Xj)=m−1∑k=1m(xki−x.i)(xkj−x.j)
分母是 m − 1 m-1 m−1是因为随机变量的数学期望未知,用“样本均值”代替,自由度减1。
3.1 利用numpy的corrcoef可以计算关系矩阵
**np.corrcoef(a)**可计算行与行之间的相关系数
**np.corrcoef(a,rowvar=0)**用于计算列与列之间的相关系数
import numpy as np
a=np.array([[1, 1, 2, 2, 3],
[2, 2, 3, 3, 5],
[1, 4, 2, 2, 3]])
a

np.corrcoef(a)

np.corrcoef(a,rowvar=0)

4 皮尔森相关系数(Pearson Correlation Coefficient)
首先看一下基本公式:
均值公式:
X ‾ = ∑ i = 1 n X i n \overline{\mathrm{X}}=\frac{\sum_{\mathrm{i}=1}^{\mathrm{n}} \mathrm{X}_{\mathrm{i}}}{\mathrm{n}} X=n∑i=1nXi
方差:
S 2 = ∑ i = 1 n ( X i − X ‾ ) 2 n − 1 \mathrm{S}^{2}=\frac{\sum_{i=1}^{\mathrm{n}}\left(\mathrm{X}_{\mathrm{i}}-\overline{\mathrm{X}}\right)^{2}}{\mathrm{n}-1} S2=n−1∑i=1n(Xi−X)2
或者:
Var ( x ) = E ( ( x − E ( x ) ) 2 ) \operatorname{Var}(x)=E\left((x-E(x))^{2}\right) Var(x)=E((x−E(x))2)
另一种形式:
Var ( x ) = E ( ( x − E ( x ) ) 2 ) = E ( x 2 − 2 x E ( x ) + ( E ( x ) ) 2 ) = E ( x 2 ) − 2 E ( x ) E ( x ) + ( E ( x ) ) 2 = E ( x 2 ) − 2 ( E ( x ) ) 2 + ( E ( x ) ) 2 = E ( x 2 ) − ( E ( x ) ) 2 \begin{aligned} \operatorname{Var}(x) &=E\left((x-E(x))^{2}\right) \\ &=E\left(x^{2}-2 x E(x)+(E(x))^{2}\right) \\ &=E\left(x^{2}\right)-2 E(x) E(x)+(E(x))^{2} \\ &=E\left(x^{2}\right)-2(E(x))^{2}+(E(x))^{2} \\ &=E\left(x^{2}\right)-(E(x))^{2} \end{aligned} Var(x)=E((x−E(x))2)=E(x2−2xE(x)+(E(x))2)=E(x2)−2E(x)E(x)+(E(x))2=E(x2)−2(E(x))2+(E(x))2=E(x2)−(E(x))2
标准差:
S = ∑ i = 1 n ( X i − X ‾ ) 2 n − 1 S=\sqrt{\frac{\sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)^{2}}{n-1}} S=n−1∑i=1n(Xi−X)2
标准差与方差不同的是,标准差和变量的计算单位相同,比方差清楚,因此很多时候我们分析的时候更多的使用的是标准差。
均值描述的是样本集合的中间点,它告诉我们的信息是有限的,而标准差给我们描述的是样本集合的各个样本点到均值的距离之平均。
标准差和方差一般是用来描述一维数据的,但现实生活中我们常常会遇到含有多维数据的数据集,最简单的是大家上学时免不了要统计多个学科的考试成绩。面对这样的数据集,我们当然可以按照每一维独立的计算其方差,但是通常我们还想了解更多。
协方差:
Cov ( x , y ) = E ( ( x − E ( x ) ) ( y − E ( y ) ) ) \operatorname{Cov}(x, y)=E((x-E(x))(y-E(y))) Cov(x,y)=E((x−E(x))(y−E(y)))
展开:
Cov ( X , Y ) = E [ ( X − E ( X ) ) ⋅ ( Y − E ( Y ) ) ] = E ( X Y ) − E [ X E ( Y ) + Y E ( X ) ] + E [ E ( X ) E = E ( X Y ) − 2 E ( X ) E ( Y ) + E ( X ) E ( Y ) = E ( X Y ) − E ( X ) E ( Y ) \begin{aligned} \operatorname{Cov}(X, Y) &=E[(X-E(X)) \cdot(Y-E(Y))] \\ &=E(X Y)-E[X E(Y)+Y E(X)]+E[E(X) E\\ &=E(X Y)-2 E(X) E(Y)+E(X) E(Y) \\ &=E(X Y)-E(X) E(Y) \end{aligned} Cov(X,Y)=E[(X−E(X))⋅(Y−E(Y))]=E(XY)−E[XE(Y)+YE(X)]+E[E(X)E=E(XY)−2E(X)E(Y)+E(X)E(Y)=E(XY)−E(X)E(Y)
特殊情况下,当X=Y时:
Cov ( X , Y ) = E ( X − E ( X ) ) 2 = E ( Y − E ( Y ) ) 2 = D ( X ) \operatorname{Cov}(X, Y)=E(X-E(X))^{2}=E(Y-E(Y))^{2}=D(X) Cov(X,Y)=E(X−E(X))2=E(Y−E(Y))2=D(X)
或者:
cov ( X , Y ) = ∑ i = 1 n ( X i − X ‾ ) ( Y i − Y ‾ ) n − 1 \operatorname{cov}(\mathrm{X}, \mathrm{Y})=\frac{\sum_{\mathrm{i}=1}^{\mathrm{n}}\left(\mathrm{X}_{\mathrm{i}}-\overline{\mathrm{X}}\right)\left(\mathrm{Y}_{\mathrm{i}}-\overline{\mathrm{Y}}\right)}{\mathrm{n}-1} cov(X,Y)=n−1∑i=1n(Xi−X)(Yi−Y)
从直观上来看,协方差表示的是两个变量总体误差的期望。
如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值时另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值;
如果两个变量的变化趋势相反,即其中一个变量大于自身的期望值时另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
如果X与Y是统计独立的,那么二者之间的协方差就是0,因为两个独立的随机变量满足 E [ X Y ] = E [ X ] E [ Y ] E[X Y]=E[X] E[Y] E[XY]=E[X]E[Y]
故协方差主要用来度量各个维度偏离其均值的程度。如果结果为正值,则说明两者是正相关的,如果结果为负值, 就说明两者是负相关,如果为0,则两者之间没有关系,互相独立。
协方差也只能处理二维问题,那维数多了自然就需要计算多个协方差,比如n维的数据集就需要计算
n ! ( n − 2 ) ! ∗ 2 \frac{n !}{(n-2) ! * 2} (n−2)!∗2n!个协方差,那自然而然我们会想到使用矩阵来组织这些数据。
协方差作为描述X和Y相关程度的量,在同一物理量纲之下有一定的作用,但同样的两个量采用不同的量纲使它们的协方差在数值上表现出很大的差异,于是引出皮尔森相关系数。
皮尔森相关系数
两个变量之间的皮尔森相关系数定义为两个变量之间的协方差和标准差的商:
Corr ( x , y ) = Cov ( x , y ) Var ( x ) Var ( y ) \operatorname{Corr}(x, y)=\frac{\operatorname{Cov}(x, y)}{\sqrt{\operatorname{Var}(x) \operatorname{Var}(y)}} Corr(x,y)=Var(x)Var(y)Cov(x,y)
几种常见形式:
公式一:
ρ X , Y = cov ( X , Y ) σ X σ Y = E ( ( X − μ X ) ( Y − μ Y ) ) σ X σ Y = E ( X Y ) − E ( X ) E ( Y ) E ( X 2 ) − E 2 ( X ) E ( Y 2 ) − E 2 ( Y ) \rho_{X, Y}=\frac{\operatorname{cov}(X, Y)}{\sigma_{X} \sigma_{Y}}=\frac{E\left(\left(X-\mu_{X}\right)\left(Y-\mu_{Y}\right)\right)}{\sigma_{X} \sigma_{Y}}=\frac{E(X Y)-E(X) E(Y)}{\sqrt{E\left(X^{2}\right)-E^{2}(X)} \sqrt{E\left(Y^{2}\right)-E^{2}(Y)}} ρX,Y=σXσYcov(X,Y)=σXσYE((X−μX)(Y−μY))=E(X2)−E2(X)E(Y2)−E2(Y)E(XY)−E(X)E(Y)
公式二:
ρ X , Y = N ∑ X Y − ∑ X ∑ Y N ∑ X 2 − ( ∑ X ) 2 N ∑ Y 2 − ( ∑ Y ) 2 \rho_{X, Y}=\frac{N \sum X Y-\sum X \sum Y}{\sqrt{N \sum X^{2}-\left(\sum X\right)^{2}} \sqrt{N \sum Y^{2}-\left(\sum Y\right)^{2}}} ρX,Y=N∑X2−(∑X)2N∑Y2−(∑Y)2N∑XY−∑X∑Y
公式三:
ρ X , Y = ∑ ( X − X ‾ ) ( Y − Y ‾ ) ∑ ( X − X ‾ ) 2 ∑ ( Y − Y ‾ ) 2 \rho_{X, Y}=\frac{\sum(X-\overline{X})(Y-\overline{Y})}{\sqrt{\sum(X-\overline{X})^{2} \sum(Y-\overline{Y})^{2}}} ρX,Y=∑(X−X)2∑(Y−Y)2∑(X−X)(Y−Y)
公式四:
ρ X , Y = ∑ X Y − ∑ X ∑ Y N ( ∑ X 2 − ( ∑ X ) 2 N ) ( ∑ Y 2 − ( ∑ Y ) 2 N ) \rho_{X, Y}=\frac{\sum X Y-\frac{\sum X \sum Y}{N}}{\sqrt{\left(\sum X^{2}-\frac{\left(\sum X\right)^{2}}{N}\right)\left(\sum Y^{2}-\frac{\left(\sum Y\right)^{2}}{N}\right)}} ρX,Y=(∑X2−N(∑X)2)(∑Y2−N(∑Y)2)∑XY−N∑X∑Y
以上列出的四个公式等价,其中E是数学期望,cov表示协方差,N表示变量取值的个数。
由公式可知,Pearson 相关系数是用协方差除以两个变量的标准差得到的,虽然协方差能反映两个随机变量的相关程度(协方差大于0的时候表示两者正相关,小于0的时候表示两者负相关),但其数值上受量纲的影响很大,不能简单地从协方差的数值大小给出变量相关程度的判断。为了消除这种量纲的影响,于是就有了相关系数的概念。
对皮尔森相关系数的通俗解释
对于协方差,可以通俗的理解为:两个变量在变化过程中是同方向变化?还是反方向变化?同向或反向程度如何?
你变大,同时我也变大,说明两个变量是同向变化的,这时协方差就是正的。
你变大,同时我变小,说明两个变量是反向变化的,这时协方差就是负的。
从数值来看,协方差的数值越大,两个变量同向程度也就越大。反之亦然。
咱们从公式出发来理解一下:
Cov ( X , Y ) = E [ ( X − μ x ) ( Y − μ y ) ] \operatorname{Cov}(X, Y)=E\left[\left(X-\mu_{x}\right)\left(Y-\mu_{y}\right)\right] Cov(X,Y)=E[(X−μx)(Y−μy)]
公式简单翻译一下是:如果有X,Y两个变量,每个时刻的“X值与其均值之差”乘以“Y值与其均值之差”得到一个乘积,再对这每时刻的乘积求和并求出均值(其实是求“期望”,但就不引申太多新概念了,简单认为就是求均值了)。
下面举个例子来说明吧:
比如有两个变量X,Y,观察t1-t7(7个时刻)他们的变化情况。
简单做了个图:分别用红点和绿点表示X、Y,横轴是时间。可以看到X,Y均围绕各自的均值运动,并且很明显是同向变化的。

这时我们发现每一时刻 X − μ x X-\mu_{x} X−μx的值与 Y − μ y Y-\mu_{y} Y−μy的值得"正负号"一定相同(如下图:比如t1时刻,他们同为正,t2时刻他们同为负)
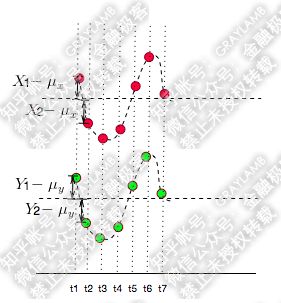
)
所以,像上图那样,当他们同向变化时, X − μ x X-\mu_{x} X−μx与 Y − μ y Y-\mu_{y} Y−μy的乘积为真。这样,当你把t1-t7时刻 X − μ x X-\mu_{x} X−μx与 Y − μ y Y-\mu_{y} Y−μy的乘积加在一起,求平均后也就是正数了。
如何反向运动呢?
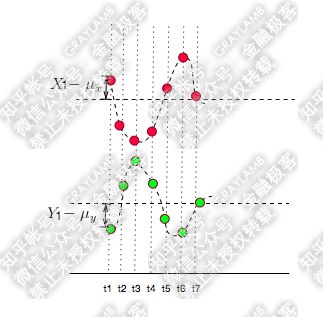
很明显, X − μ x X-\mu_{x} X−μx与 Y − μ y Y-\mu_{y} Y−μy的值得"正负号"一定相反,于是 X − μ x X-\mu_{x} X−μx与 Y − μ y Y-\mu_{y} Y−μy的乘积就是负值了。这样当你把 X − μ x X-\mu_{x} X−μx与 Y − μ y Y-\mu_{y} Y−μy的乘积加在一起,求平均的时候也就是负数了。
当然上面说的是两种特殊情况,很多时候X,Y的运动是不规律的,比如:

这时,很可能某一时刻, X − μ x X-\mu_{x} X−μx与 Y − μ y Y-\mu_{y} Y−μy的值乘积为正,另外一个时刻, X − μ x X-\mu_{x} X−μx与 Y − μ y Y-\mu_{y} Y−μy的乘积值为负。
将每一时刻, X − μ x X-\mu_{x} X−μx与 Y − μ y Y-\mu_{y} Y−μy的乘积加在一起,其中的正负项就会抵消掉,最后求平均得出的值就是协方差,通过协方差的数值大小,就可以判断这两个变量同向或者反向的程度了。
所以t1-t7时刻中,, X − μ x X-\mu_{x} X−μx与 Y − μ y Y-\mu_{y} Y−μy的乘积为正的越多,说明同向变化的次数越多,也即同向程度越高。反之亦然。
总结一下,如果协方差为正,说明X,Y同向变化,协方差越大说明同向程度越高;如果协方差为负,说明X,Y反向运动,协方差越小说明反向程度越高。
那如果X,Y同向变化,但X大于均值,Y小于均值,那么 X − μ x X-\mu_{x} X−μx与 Y − μ y Y-\mu_{y} Y−μy的乘积为负值吗?这不是矛盾了了吗?
这种情况是有可能的,比如:

可以看到,t1时刻, X − μ x X-\mu_{x} X−μx与 Y − μ y Y-\mu_{y} Y−μy的符号相反,他们的乘积为负值。
但是,总体看,这两个变量的协方差仍然是正的,因为你还要计算t2,t3,…t7时刻 X − μ x X-\mu_{x} X−μx与 Y − μ y Y-\mu_{y} Y−μy的乘积,然后再把这7个时刻的乘积求和做平均,才是最后X,Y的协方差。1个负、6个正,显然最后协方差很大可能是正的。
所以,t1时刻 X − μ x X-\mu_{x} X−μx与 Y − μ y Y-\mu_{y} Y−μy的乘积为负值,并不能说明他们反向运动,要结合整体的情况来判断。
那么,你可能又要问了,既然都是同向变化,那t1时刻 X − μ x X-\mu_{x} X−μx与 Y − μ y Y-\mu_{y} Y−μy的乘积为负值,其他时刻乘积为正的这种情况下,与t1-t7时刻 X − μ x X-\mu_{x} X−μx与 Y − μ y Y-\mu_{y} Y−μy的乘积均为正值的情况下,到底有什么差异呢?这点其实前面已经解释过了,差异就是:第一种情况的同向程度不如第二种情况的同向程度大(第一种情况6正1负,第二种情况7正,所以第一种情况的协方差小于第二种情况的协方差,第一种情况X,Y变化的同向程度要小于第二种情况).
另外,如果你还钻牛角尖,说如果t1,t2,t3……t7时刻X,Y都在增大,而且X都比均值大,Y都比均值小,这种情况协方差不就是负的了?7个负值求平均肯定是负值啊?但是X,Y都是增大的,都是同向变化的,这不就矛盾了?
这个更好解释了:这种情况不可能出现!
因为,你的均值算错了……
X,Y的值应该均匀的分布在均值两侧才对,不可能都比均值大,或都比均值小。
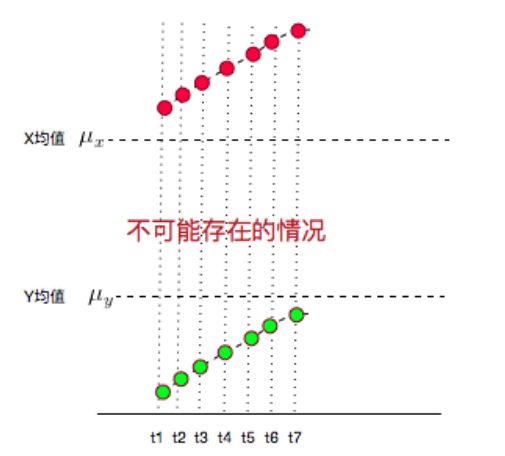
所以,实际它的图应该是下面这样的:

发现没有,又变成 X − μ x X-\mu_{x} X−μx与 Y − μ y Y-\mu_{y} Y−μy的符号相同的情况了。
对于相关系数,我们从它的公式入手。一般情况下,相关系数的公式为:
ρ = Cov ( X , Y ) σ X σ Y \rho=\frac{\operatorname{Cov}(X, Y)}{\sigma_{X} \sigma_{Y}} ρ=σXσYCov(X,Y)
就是用X、Y的协方差除以X的标准差和Y的标准差。
所以,相关系数也可以看成协方差:一种剔除了两个变量量纲影响、标准化后的特殊协方差。
既然是一种特殊的协方差,那它:
1、也可以反映两个变量变化时是同向还是反向,如果同向变化就为正,反向变化就为负。
2、由于它是标准化后的协方差,因此更重要的特性来了:它消除了两个变量变化幅度的影响,而只是单纯反应两个变量每单位变化时的相似程度。
比较抽象,下面还是举个例子来说明:
首先,还是承接上文中的变量X、Y变化的示意图(X为红点,Y为绿点),来看两种情况:

很容易就可以看出以上两种情况X,Y都是同向变化的,而这个“同向变化”,有个非常显著特征:X、Y同向变化的过程,具有极高的相似度!无论第一还是第二种情况下,都是:t1时刻X、Y都大于均值,t2时刻X、Y都变小且小于均值,t3时刻X、Y继续变小且小于均值,t4时刻X、Y变大但仍小于均值,t5时刻X、Y变大且大于均值……
可是,计算一下他们的协方差,
第一种情况下:
[ ( 100 − 0 ) × ( 70 − 0 ) + ( − 100 − 0 ) × ( − 70 − 0 ) + ( − 200 − 0 ) × ( − 200 − 0 ) … ] ÷ 7 ≈ 15428 [(100-0) \times(70-0)+(-100-0) \times(-70-0)+(-200-0) \times(-200-0) \dots] \div 7 \approx 15428 [(100−0)×(70−0)+(−100−0)×(−70−0)+(−200−0)×(−200−0)…]÷7≈15428
第二种情况下:
[ ( 0.01 − 0 ) × ( 70 − 0 ) + ( − 0.01 − 0 ) × ( − 70 − 0 ) + ( − 0.02 − 0 ) × ( − 200 − 0 ) … ] ÷ 7 ≈ 1.5428 [(0.01-0) \times(70-0)+(-0.01-0) \times(-70-0)+(-0.02-0) \times(-200-0) \dots] \div 7 \approx 1.5428 [(0.01−0)×(70−0)+(−0.01−0)×(−70−0)+(−0.02−0)×(−200−0)…]÷7≈1.5428
协方差差出了一万倍,只能从两个协方差都是正数判断出两种情况下X、Y都是同向变化,但是,一点也看不出两种情况下X、Y的变化都具有相似性这一特点。
这是为什么呢?
因为以上两种情况下,在X、Y两个变量同向变化时,X变化的幅度不同,这样,两种情况的协方差更多的被变量的变化幅度所影响了。
所以,为了能准确的研究两个变量在变化过程中的相似程度,我们就要把变化幅度对协方差的影响,从协方差中剔除掉。于是,相关系数就横空出世了,就有了最开始相关系数的公式:
ρ = Cov ( X , Y ) σ X σ Y \rho=\frac{\operatorname{Cov}(X, Y)}{\sigma_{X} \sigma_{Y}} ρ=σXσYCov(X,Y)
那么为什么要通过除以标准差的方式来剔除变化幅度的影响呢?咱们简单从标准差公式看一下:
σ X = E ( ( X − μ x ) 2 ) \sigma_{X}=\sqrt{E\left(\left(X-\mu_{x}\right)^{2}\right)} σX=E((X−μx)2)
从公式可以看出,标准差计算方法为,每一时刻变量值与变量均值之差再平方,求得一个数值,再将每一时刻这个数值相加后求平均,再开方。

那为什么要对它做平方呢?因为有时候变量值与均值是反向偏离的(见下图), X − μ x X-\mu_{x} X−μx是一个负数,平方后,就可以把负号消除了。这样在后面求平均时,每一项数值才不会被正负抵消掉,最后求出的平均值才能更好的体现出每次变化偏离均值的情况。

当然,最后求出平均值后并没有结束,因为刚才为了消除负号,把 X − μ x X-\mu_{x} X−μx进行了平方,那最后肯定要把求出的均值开方,将这个偏离均值的幅度还原回原来的量级。于是就有了下面标准差的公式:
σ X = E ( ( X − μ x ) 2 ) \sigma_{X}=\sqrt{E\left(\left(X-\mu_{x}\right)^{2}\right)} σX=E((X−μx)2)
所以标准差描述了变量在整体变化过程中偏离均值的幅度。协方差除以标准差,也就是把协方差中变量变化幅度对协方差的影响剔除掉,这样协方差也就标准化了,它反应的就是两个变量每单位变化时的情况。这也就是相关系数的公式含义了。
同时,你可以反过来想象一下:既然相关系数是协方差除以标准差,那么,当X或Y的波动波动幅度变大时,它们的协方差会变大,标准差也会变大,这样相关系数的分子分母都变大,其实变大的趋势会被抵消掉,变小时也亦然。于是,很明显的,相关系数不像协方差一样可以在 + ∞ +\infty +∞到 − ∞ -\infty −∞之间变化,它只能在+1到-1之间变化(相关系数的取值范围在+1到-1之间可以通过施瓦茨不等式来证明)
总结一下,对于两个变量X、Y,
当他们的相关系数为1时,说明两个变量变化时的正向相似度最大,即,你变大一倍,我也变大一倍;你变小一倍,我也变小一倍。也即是完全正相关(以X、Y为横纵坐标轴,可以画出一条斜率为正数的直线,所以X、Y是线性关系的)。
随着他们相关系数减小,两个变量变化时的相似度也变小,当相关系数为0时,两个变量的变化过程没有任何相似度,也即两个变量无关。
当相关系数继续变小,小于0时,两个变量开始出现反向的相似度,随着相关系数继续变小,反向相似度会逐渐变大。
当相关系数为-1时,说明两个变量变化的反向相似度最大,即,你变大一倍,我变小一倍;你变小一倍,我变大一倍。也即是完全负相关(以X、Y为横纵坐标轴,可以画出一条斜率为负数的直线,所以X、Y也是线性关系的)。
有了上面的背景,我们再回到最初的变量X、Y的例子中,可以先看一下第一种情况的相关系数:

X的标准差为
σ X = E ( ( X − μ x ) 2 ) = [ ( 100 − 0 ) 2 + ( − 100 − 0 ) 2 ⋯ ] ÷ 7 ≈ 130.9307 \sigma_{X}=\sqrt{E\left(\left(X-\mu_{x}\right)^{2}\right)}=\sqrt{\left[(100-0)^{2}+(-100-0)^{2} \cdots\right] \div 7} \approx 130.9307 σX=E((X−μx)2)=[(100−0)2+(−100−0)2⋯]÷7≈130.9307
Y的标准差为:
σ Y = E ( ( Y − μ y ) 2 ) = [ ( 70 − 0 ) 2 + ( − 70 − 0 ) 2 ⋯ ] ÷ 7 ≈ 119.2836 \sigma_{Y}=\sqrt{E\left(\left(Y-\mu_{y}\right)^{2}\right)}=\sqrt{\left[(70-0)^{2}+(-70-0)^{2} \cdots\right] \div 7} \approx 119.2836 σY=E((Y−μy)2)=[(70−0)2+(−70−0)2⋯]÷7≈119.2836
X和Y的协方差为:
[ ( 100 − 0 ) × ( 70 − 0 ) + ( − 100 − 0 ) × ( − 70 − 0 ) + ( − 200 − 0 ) × ( − 200 − 0 ) … ] ÷ 7 ≈ 15428 [(100-0) \times(70-0)+(-100-0) \times(-70-0)+(-200-0) \times(-200-0) \dots] \div 7 \approx 15428 [(100−0)×(70−0)+(−100−0)×(−70−0)+(−200−0)×(−200−0)…]÷7≈15428
于是相关系数为:
ρ = 15428.57 ÷ ( 130.9307 × 119.2836 ) ≈ 0.9879 \rho=15428.57 \div(130.9307 \times 119.2836) \approx 0.9879 ρ=15428.57÷(130.9307×119.2836)≈0.9879
说明第一种情况下,X的变化与Y的变化具有很高的相似度,而且已经接近完全正相关了,X、Y几乎就是线性变化的。
那第二种情况呢?
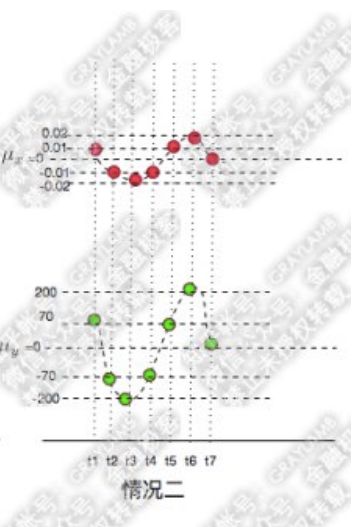
X的标准差为:
σ X = E ( ( X − μ x ) 2 ) = [ ( 0.01 − 0 ) 2 + ( − 0.01 − 0 ) 2 ⋯ ] ÷ 7 ≈ 0.01309307 \sigma_{X}=\sqrt{E\left(\left(X-\mu_{x}\right)^{2}\right)}=\sqrt{\left[(0.01-0)^{2}+(-0.01-0)^{2} \cdots\right] \div 7} \approx 0.01309307 σX=E((X−μx)2)=[(0.01−0)2+(−0.01−0)2⋯]÷7≈0.01309307
Y的标准差为:
σ Y = E ( ( Y − μ y ) 2 ) = [ ( 70 − 0 ) 2 + ( − 70 − 0 ) 2 ⋯ ] ÷ 7 ≈ 119.2836 \sigma_{Y}=\sqrt{E\left(\left(Y-\mu_{y}\right)^{2}\right)}=\sqrt{\left[(70-0)^{2}+(-70-0)^{2} \cdots\right] \div 7} \approx 119.2836 σY=E((Y−μy)2)=[(70−0)2+(−70−0)2⋯]÷7≈119.2836
X和Y的协方差:
[ ( 0.01 − 0 ) × ( 70 − 0 ) + ( − 0.01 − 0 ) × ( − 70 − 0 ) + ( − 0.02 − 0 ) × ( − 200 − 0 ) … ] ÷ 7 ≈ 1.5428 [(0.01-0) \times(70-0)+(-0.01-0) \times(-70-0)+(-0.02-0) \times(-200-0) \dots] \div 7 \approx 1.5428 [(0.01−0)×(70−0)+(−0.01−0)×(−70−0)+(−0.02−0)×(−200−0)…]÷7≈1.5428
于是相关系数为:
ρ = 1.542857 ÷ ( 0.01309307 × 119.2836 ) ≈ 0.9879 \rho=1.542857 \div(0.01309307 \times 119.2836) \approx 0.9879 ρ=1.542857÷(0.01309307×119.2836)≈0.9879
说明第二种情况下,虽然X的变化幅度比第一种情况X的变化幅度小了10000倍,但是丝毫没有改变“X的变化与Y的变化具有很高的相似度”这一结论。同时,由于第一种、第二种情况的相关系数是相等的,因此在这两种情况下,X、Y的变化过程有着同样的相似度。
皮尔森相关系数的主要性质
1、有界性
相关系数的取值范围为-1到1,其可以看成是无量纲的协方差。
2、统计意义
值越接近1,说明两个变量正相关性(线性)越强,越接近-1,说明负相关性越强,当为0时表示两个变量没有相关性。
试用场景
当两个变量的标准差都不为零时,相关系数才有意义,皮尔逊相关系数适用于:
-
两个变量之间是线性关系,都是连续数据。
-
两个变量的总体是正态分布,或接近正态的单峰分布。
-
两个变量的观测值是成对的,每对观测值之间相互独立
注:在时间序列领域的自相关函数ACF是类似的计算公式,可用于ARIMA模型平稳性判定和模型定阶
代码实现:
这里我们计算皮尔森系数的公式用到的是公式四:
ρ X , Y = ∑ X Y − ∑ X ∑ Y N ( ∑ X 2 − ( ∑ X ) 2 N ) ( ∑ Y 2 − ( ∑ Y ) 2 N ) \rho_{X, Y}=\frac{\sum X Y-\frac{\sum X \sum Y}{N}}{\sqrt{\left(\sum X^{2}-\frac{\left(\sum X\right)^{2}}{N}\right)\left(\sum Y^{2}-\frac{\left(\sum Y\right)^{2}}{N}\right)}} ρX,Y=(∑X2−N(∑X)2)(∑Y2−N(∑Y)2)∑XY−N∑X∑Y
import math
def perarson(vector1,vector2):
n=len(vector1)
# simple sums
sum1=sum(float(vector1[i]) for i in range(n))
sum2=sum(float(vector2[i]) for i in range(n))
# sum up the squares
sum1_pow=sum([pow(v,2.0) for v in vector1])
sum2_pow=sum([pow(v,2.0) for v in vector2])
# sum up the products
p_sum=sum([vector1[i]*vector2[i] for i in range(n)])
#分子num,分母den
num=p_sum-(sum1*sum2/n)
den=math.sqrt((sum1_pow-pow(sum1,2)/n)*(sum2_pow-pow(sum2,2)/n))
if den==0:
return 0.0
return num/den
x = [0,1,0,3]
y = [0,1,1,1]
perarson(x,y)
结果x和y的相关系数是0.47140452079103173.
5 参考文献
1.https://blog.csdn.net/cymy001/article/details/79576019
2.https://www.cnblogs.com/renpfly/p/9555959.html
3.https://blog.csdn.net/zh11403070219/article/details/82385057
4.http://www.cnblogs.com/ryuham/p/4764015.html