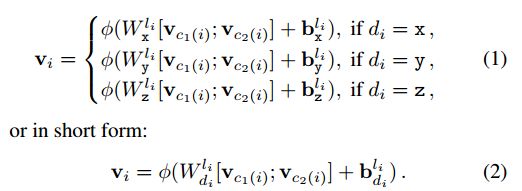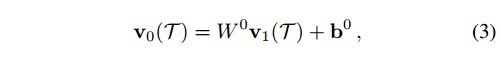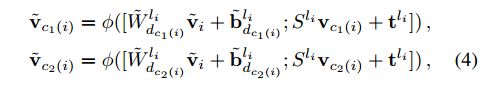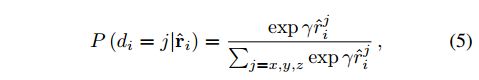细胞逃逸:用于三维点云模型识别的深Kd-Networks
文章原名:Escape from Cells: Deep Kd-Networks for the Recognition of 3D Point Cloud Models
文章地址:https://www.researchgate.net/publication/315797207_Escape_from_Cells_Deep_Kd-Networks_for_The_Recognition_of_3D_Point_Cloud_Models
摘要
我们提出了一个新的深度学习架构(称为Kdnetwork),它被设计用于3D模型识别任务,并且用于非结构化点云。新的体系结构执行乘法变换,并根据kdtree对点云进行细分来共享这些变换的参数。不同于目前主流的卷积结构,通常需要在均匀的二维或三维网格上进行光栅化,Kd-网络不以任何方式依赖于这样的网格,因此避免了不良的缩放行为。在一系列使用流行形状识别基准的实验中,Kd-网络在形状分类、形状检索和形状部分分割等形状识别任务中显示出具有竞争力的性能。
1。介绍
随着我们周围的3D世界正在被扫描和数字化,随着人类设计模型的档案越来越大,3D几何模型的识别和分析变得越来越重要。同时,深卷积网络(ConvNets)[15]在解决二维图像数据的类似识别任务方面也做得很好。因此,很自然地,目前许多研究旨在使深层ConvNets适应3D模型[36、18、4、35、34、21、31、2、3]。
这种适应不是微不足道的。实际上,使ConvNets适用于3D数据的最直接的方法是将3D模型光栅化到统一的体素网格上。然而,这种方法会导致过大的内存占用和缓慢的处理时间。因此,遵循这条路径[36、18、4、35、34、16]的工作使用小的空间分辨率(例如,64×64×64),这明显落后于处理2D数据典型的网格分辨率,并且很可能不足以完成需要注意模型中的细节的识别任务。
为了解决这个问题,我们从计算机图形学和计算几何社区的长期研究历史中得到启发[25,10],其中已经提出了大量比均匀网格可伸缩的索引结构,包括kd-树[1]、八叉树[19]、二元空间划分树[28]、R-树[11]、con。我们的工作是基于这样的问题,即这些索引结构中的至少一些是否适合形成深层结构的基础,就像均匀网格形成卷积网络中的计算、数据对齐和参数共享的基础一样。
在这项工作中,我们选择一种最常见的3D索引结构(kd-tree[1])并设计一个深层结构(Kd-network),它在许多方面模仿ConvNets,但是使用kd-tree结构来形成计算图,共享可学习的参数,以及计算前馈底层fashi中的分层表示序列。在。在一系列实验中,我们发现Kdnetworks在分类、检索和零件分割等识别操作的精度方面接近(甚至超过)ConvNets。同时,由于与均匀体素网格相比,kd-树索引和结构3D数据的能力有所提高,Kdnetwork在火车和测试时具有更小的内存占用和更有效的计算。
下面,我们首先回顾第二节中关于三维模型的卷积网络的相关工作。然后,在第3节中讨论Kd-网络体系结构。第4节对玩具数据(MNIST的变体)和标准基准(ModelNet10、ModelNet40、SHREC’16、ShapeNet部件数据集)进行了广泛的评估。我们在第5节总结了工作
2。相关工作
几个小组研究了ConvNets在均匀三维网格上三维模型光栅化中的应用[36,18]。这些改进包括生成性架构和非常深层区分性架构的组合[4,35]。尽管在粗粒度分类中取得了相当大的成功,但是依赖于统一的3D网格来表示数据,使得这种用于细粒度任务和高空间表示的方法的扩展存在问题。为了提高可伸缩性,[34,16]已经考虑了定义卷积的稀疏方法,同时仍然使用统一的3D网格来表示。
另一种方法[31,21]是避免使用3D网格,而是将二维ConvNets应用于3D对象的2D投影,同时汇集对应于不同视图的表示。尽管效率有所提高,但是由于与投影操作相关的信息丢失,这种方法对于硬3D形状识别任务可能不是最佳的。一组方法(如谱ConvNets[6,2]和各向异性ConvNets[3])将ConvNets推广到非欧几里德几何,如网格表面。虽然这些算法在标准形状识别和检索基准上的性能尚未被报道,但它们在局部对应/匹配任务中显示出非常好的性能。Kd-网络以及PointNet架构[20]直接与点一起工作,因此可以将用内部ConvNets计算的表示作为输入。这种配置可能结合了外部和内部ConvNets的至少一些优点,但是它的研究仍留待以后的工作。
除了下文详细讨论的它们与卷积网络的连接之外,Kd-网络与递归神经网络有关[30]。递归神经网络和Kd网络都有树形结构的计算图。然而,前者跨计算树图中的所有节点共享参数,而Kd-网络中的参数共享更具有结构化,这使得它们能够实现竞争性能。
最后,与我们并行开发的两种方法有着重要的相似之处。OctNets[23]是在非均匀网格(浅OctTrees)上操作的修改ConvNets,因此具有使用非均匀网格的相同思想
深层建筑内的空间结构。更相关的是基于图的ConvNets,带有边缘相关滤波器[29]。Kd-网络可以被视为其体系结构的特定实例,其中kd-树是底层图(而[29]评估了用于点云分类的最近邻图)。Kd-net在ModelNet基准测试上优于[23]和[29]中的设置,这表明基于kd-tree的深层架构可能特别适合于粗略级别的形状分类。
三。基于Kd-网络的形状识别
现在我们介绍Kd-网络,从讨论它们的输入格式(一定大小的kd-树)开始,然后讨论Kd-网络每种表示的自底向上计算,最后讨论有监督的参数学习。
3.1。输入
新的深层架构(Kd-network)与针对3D点云构建的kd-tree一起工作。Kd-网络还可以考虑和利用单个输入点(如颜色、反射率、法线方向)的特性。在列车运行时,Kd-网络与固定大小的点云一起工作,N=2D(不同大小的点云可以通过子采样或过采样减小到这种大小)。通过选取具有最大范围(跨度)点坐标的坐标轴,并将点集分割成两个大小相等的子集,然后递归到每个子集,以自上而下的方式递归地构造kd-tree。结果,产生了包含N_1=2D_1个非叶节点的深度D的平衡kd-树T。
因此,每个非叶节点Vi∈T与三个分裂方向di(沿着x、y或z轴,即di∈{x,y,z})中的一个和某个分裂位置(阈值)i相关联。树节点还具有水平li∈{1,...,D_1}的特征,其中对于根节点li=1,对于包含单个3D点的树叶,li=D。我们假设平衡树中的节点是以标准自顶向下的方式编号的,根节点是第一个节点,第i个节点
具有数字c1(i)=2i和c2(i)=2i+1的子节点的。
3.2。用Kd网络处理数据
给定输入kd-树T,预训练Kd-网络计算与树的每个节点相关联的向量表示vi。对于叶子节点,这些表示被给出为描述与这些叶子相关联的各个点的k维向量。与非叶节点对应的表示是以自底向上的方式计算的(图1)。考虑在级别l(i)上的非叶节点i,其中子节点c1(i)和子节点c2(i)在级别l(i)+1,对于该节点,已经计算了表示vc1(i)和vc2(i)。然后,向量表示vi计算如下:
这里,φ(·)是一些非线性(例如,修正线性单位φ(a)=max(a,0)),方括号表示级联。(1)中的仿射变换由Li层的可学习参数{Wxli,WYLI,WZLI,BL XI,BL YI,BL Zi}定义。因此,根据节点的分裂方向di,应用三个仿射变换中的一个,然后应用简单的非线性。
矩阵和偏置向量的维数由维数m1、m2、.…在树的每个层次上的表示mD。因此,在第十级的W x l、W y l和W l z矩阵具有维数ml×2ml+1(请记住这些水平是从根到叶的编号),并且偏置向量bl x、bl y、bl z具有维数ml。
一旦变换(1)以底部顺序被应用,则获得样本T的根表示v1(T)。当然,它可以通过几个额外的线性和非线性变换(“全连接层”)。在我们的分类实验中,我们使用v1(T)表示作为输入直接学习线性分类器。在这种情况下,分类网络输出非规范化类概率的向量:
其中,W 0和b0是最终的线性多分类器的参数。
3.3。学习分类
Kd-网络是一种前馈神经网络,它具有在D_1非叶层j∈{1..D_1}的每个D_1非叶层上的可学习参数{W x j、W y j、W z j、bj x、bj y、bj z},以及用于最终分类器的可学习参数{W 0,b0}。标准反向传播法可用于计算损耗函数w.r.t.网络参数的梯度。因此,可以使用标准随机优化算法和标准损耗,例如网络输出v0(T)(3)上的交叉熵,从标记kd-树的数据集学习网络参数。
3.4。学会检索
学习表示(3)不是为了产生类概率,而是为了产生描述形状并且可以用于检索的特定维度的描述符向量。然后,可以使用任何观察匹配(例如,同类)和非匹配(例如,不同类)形状的示例的嵌入学习损耗,使用反向传播来学习Kd-网络的参数。
在我们的实验中,我们使用最近提出的直方图损失[33],但是也可以使用更传统的损失,例如暹罗损失[5,8]或三重损失[27]。
3.5。Kd-网络的性质
这里我们讨论了Kd-网络的性质,并将它们与ConvNets的一些性质联系起来。
分层参数共享。与ConvNets类似,Kd-网络通过应用与非线性交织的并行空间局部化乘法运算序列来处理输入。重要的是,正如ConvNets在不同空间位置共享用于局部化乘法(卷积核)的参数一样,Kd-网络也共享树级j所有节点上的乘法参数{Wxj、Wyj、Wzj、bj x、bj y、bj z}。
分层表示。ConvNets应用底层处理,并计算与渐进的大部分图像相对应的表示序列。该过程是分级的,在某种意义上,某一层的空间位置的表示是使用线性和非线性操作从前一层的多个周围位置的表示中获得的。所有这些都是在Kd-网络中模拟的,唯一的不同之处在于,在同一kd-树级别的两个不同节点的接收字段是不重叠的。
抖动的部分不变性。已知使用池操作和/或大于一个的步长的卷积网络对输入中的小空间抖动具有部分不变性。Kd-网络对这种抖动也是不变的(除非这种抖动强烈干扰叶节点的表示)。这是因为键正向传播操作(1)忽略了分裂阈值i。s)。
旋转不变性。与ConvNets类似,Kd-网络对旋转不是不变的,因为底层的kd-树对旋转不是不变的。在这个方面,Kd-网络比本征ConvNets[6,2,3]差。处理可变方向的标准技巧包括预对齐(使用预测数据[13,20]的几何变换的启发式或网络分支)以及合并增强[14](或简单地进行过度增强训练)。
kd-树结构的作用。底层kd-树在Kd-网络数据处理过程中的作用是双重的。首先,底层的kd-tree确定哪些叶子表示被组合/合并在一起,以及按照什么顺序。其次,底层kd-tree的结构可以被看作形状描述符本身(图2),因此不管叶子表示是什么,它都充当信息的源。然后,Kdnetwork用作提取kd-tree结构中包含的形状信息的机制。如将在实验中揭示的,第二个方面是相当重要的,因为即使在没有有意义的叶子表示的情况下,Kd-网络也能够仅仅基于kd-树结构很好地识别形状。
3.6。分段扩展
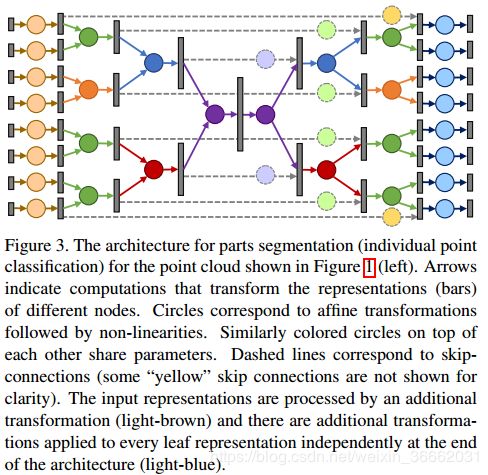
Kd-网络架构可以扩展为以与ConvNets相同的方式执行语义/部件分割任务。在本工作中,我们模仿了ConvNets在[17,24]中提出的具有跳过连接的编码器-解码器(沙漏形)结构(图3)。表示通过设置v 1=v1(或通过一个或多个完全连接的层获得v 1)然后使用以下自顶向下计算链进行:
其中,W_dc(i)和b_lidc(i)是仿射变换的参数,该仿射变换将父表示映射到彼此叠加的子表示,而Sli和tli是从v c1(i)到v_c1(i)(以及从v c2(i)到v_c2(i))的跳过连接内的仿射变换的参数。在我们的实现中,前一组参数取决于拆分方向,而后一组仅依赖于节点层。
为了增加模型的容量,可以在体系结构的开始或体系结构的末尾插入具有非线性交织的附加乘法层(具有跨叶共享的参数,使得这些层类似于ConvNets中的1×1-卷积)。此外,可以在瓶颈处插入完全连接的乘法层。
3.7。实现细节
叶子表示。如上所述,对于叶节点i,可以用几种方式定义表示vi。在我们的实验中,除非另有说明,我们使用通过将形状的质心放在原点并重新标定输入点云来拟合[1;1]33D框而获得的归一化3D坐标。
数据扩充。与其他机器学习结构类似,Kd-网络的性能可以通过训练数据扩充来提高。下面,我们尝试将扰动几何变换应用于3D点云。此外,我们发现将随机性注入到kd-树结构中非常有用。为此,我们使用以下概率随机化分裂方向的选择:
其中ri是归一化为单位和的范围的向量。
4。实验
现在我们讨论Kdnetworks在形状分类、形状检索和零件分割任务基准测试中的应用结果。对于分类,我们还评估了Kd-网络的几种变化和消融。我们使用The.[32]和Lasagne[9]实现Kd网络,以及额外的定性和定量结果可在项目网页1获得。
4.1。形状分类
数据集和数据处理。我们在2D的数据集(为了说明的目的)和3D点云上评估Kdnetworks。通过将非零像素的中心转换为2D点,从MNIST数据集[15]中产生2D点云。然后,从所得到的一组点中采样所需大小的点云,并添加一个小的随机噪声。图2显示了生成的点云的示例。
使用ModelNet[36](ModelNet10和ModelNet40)基准的10类和40类变化,分别包含4899和12311个模型,用于3D形状分类。两个数据集被分成训练集(3991和9843模型)和测试集(分别是909和2468模型)。在此情况下,计算三维点云如下:首先,给定数量的人脸以与其表面积成比例的概率进行采样。然后,对采样的面部取一个随机点。因此,整个采样过程近似于模型表面的均匀采样。
培训和测试程序。此外,我们通过应用几何扰动和噪声对每个对象进行预处理(如下所述)。构造确定性或随机化的kd-树,最后使用所得的点云和叶表示在Kd-网络中执行前向后传递。在测试时,我们使用与在训练中使用的相同的增强,并在十次运行中平均预测类概率。
我们实验了以下扩展:(i)在归一化坐标系下,沿每个轴(TR)的比例平移(高达±0.1);在两个水平轴(AS)上按从0.66到1.5范围取样的数目进行比例各向异性重标定。更多的全局增强,如翻转或旋转,并不能改善结果。此外,我们评估了确定性(DT)和随机(RT)kd-树。对于我们的实验,我们把(5)中的参数γ固定为10。
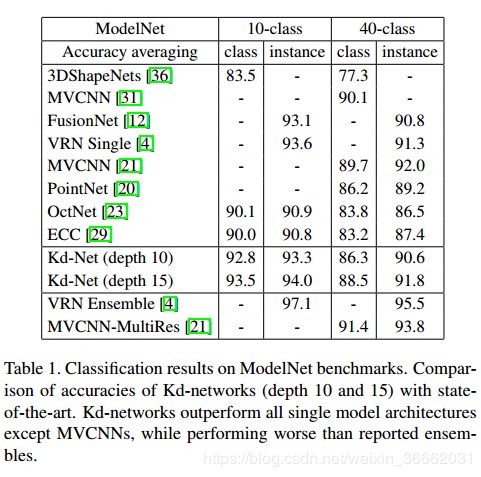
基准分类性能。我们将我们的方法与表1中的ModelNet10和ModelNet40基准测试中的最新技术进行比较。给出了用深度为10和深度为15的kd树得到的结果。对于深度10,我们的架构首先通过仿射变换从初始点坐标获得大小为32的叶子表示,该仿射变换具有在交织有ReLU非线性的所有输入点共享的参数,然后Kd-网络获得大小的中间表示:32_64_64_128_128_256_512_512_128。点云的结果表示直接用于获得具有单个完全连接层的类后验信息。对于深度15,通过将叶子表示的大小更改为8并通过中间表示大小的更新级数来修改先前的体系结构:16_16_32_32_64_64_128_128_256_256_512_1024_128。
在这两种情况下,我们使用基于平移和基于各向异性缩放的扩展,以及在测试和训练时随机生成kd-tree。注意,尽管使用随机增量,但是针对每个情况(深度10和深度15)评估了单个模型(即一组模型权重)。除了MVCNN之外,我们的结果在这些基准测试上优于所有以前的单模型结果。虽然比报道的集合更糟糕,但是Kd网络可以更快地训练。VRN集成包括6个模型,每个模型在NVidia Titan X上训练6天。我们的深度-10模型可以在16小时内训练,我们的深度-15模型可以使用一个老的NVidia Titan Black在5天内训练。此外,75%以上的时间用于点云采样和kd-树拟合,而训练本身花费的时间不到上述时间的四分之一。
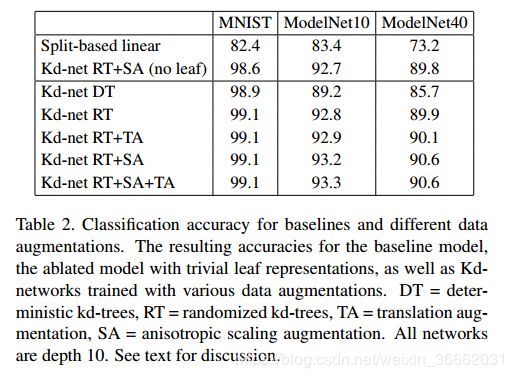
还值得注意的是,MNIST数据集上的Kdnetworks的性能达到了99.1%(表2),这与ConvNets获得的结果(没有附加的技巧)大致相同。
消融和变体。Kd网络使用关于每个对象的两个信息来源,即叶子表示和分裂的方向。注意,在分类中不使用分割坐标。我们使用两个基线评估两个信息源的相对重要性。首先,我们考虑2D和3D点云的基线,这些点云从它们的kd-树中编码分离信息,其方式如下:每个层次上的每个分离都是一个热编码,并连接到得到的特征向量。然后,我们在这种表示上使用线性分类器(图2中也显示为红/蓝条)。该基线评估只需要很少的努力就可以从分割方向信息中恢复多少信息。
除了删除第一个源信息之外,我们还评估了与完整方法相对应的模型消融。为此,我们使每个叶子表示等于一维向量(即标量),该向量等于一,从而有效地去除了第一信息源。
表2中的结果表明,第一(线性分类)基线的性能比Kd-网络(即使没有叶子信息)差得多,这表明Kd-网络的多级分层数据流和复杂的权重共享机制发挥了重要作用(注意,然而,该基线的性能明显优于c增强,表明kd-树中分裂的方向可以作为形状描述符)。最有趣的是,最新版本的Kd-网络非常接近完整方法,突出了第二信息源(分割方向)在重要性方面支配第一信息源(确认kd-树对于形状描述的适用性)。
最后,在表2中,我们评估了两种不同的增强的重要性以及随机树和确定性树的相对性能。这些实验表明kd-tree的随机化显著地提高了性能(泛化),而几何增强的效果更小。
Kd-树深度实验。为了更好地理解深度的影响,我们还进行了一系列实验,分别对应于深度小于或等于10的不同树(图4)。为了获得较小深度的Kd网络体系结构,我们只需从十层深度体系结构(如上所述)中删除初始层。
除了饱和性能外,我们发现对于较小的模型,每个阶段的学习时间变得非常短,但是实现收敛的阶段的数量增加。对于较大的模型,kd-tree构造(以及点采样)的时间成为我们实施的瓶颈。
在存在非均匀采样和抖动时退化。我们还测量了在非均匀采样和抖动存在下Kdnetworks的降解,并提供了补充材料的结果。总体而言,ModelNet10基准测试中这两种效果的降低令人惊讶地优雅。
4.2。形状检索
数据集和数据处理。为了评估3D形状检索任务,我们使用ShapeNetCore数据集[7]。ShapeNetCore是具有手动验证的类别注释和对齐的3D形状的完整ShapeNet数据集的子集。它由51300个独特的3D形状组成,分成55个类别,每个类别由它的三角形网格表示。对于我们的实验,我们使用了数据集的分布以及由3D形状检索竞赛2016(SHREC16)[26]的组织者提供的训练/验证/测试分割。除了对齐的形状之外,这个分布还包含数据集的扰动版本,它由每个随机旋转扰动的相同形状组成。此外,还有一个附加的划分,分为几个子类别可用于每个类别。在我们的实验中,我们对两个版本的数据集进行评估。
培训和测试程序。我们使用两阶段训练程序来完成目标检索任务。首先,训练网络按照上述方式进行分类任务。其次,去除预测类后验的网络的最后一层,结果点云的表示被规范化,并且用作形状描述符,为具有直方图损失的网络的微调提供。使用大小为110的小批量进行训练,每个小批量包含来自数据集的每个类别的两个随机选择的形状。利用几何扰动和kdtree随机化进行训练和预测。扩充的参数取自分类任务。为了提高每个模型在测试时的稳定性和预测质量,在归一化之前,对多个(本实验中为16个)随机kd-树中的描述符进行平均。
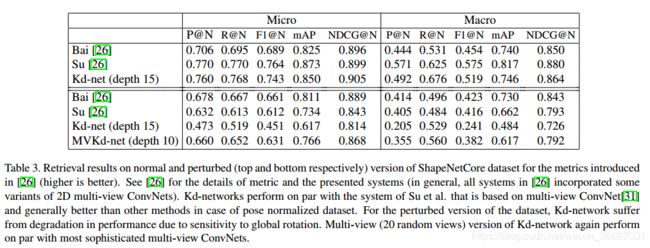
基准检索性能。我们将我们的结果表3与SHREC’16的参与者对ShapeNetCore的正常版本和干扰版本的结果进行比较。SHREC'16挑战的大多数参与团队使用基于多视图2DConvNets的系统。我们使用[26]中引入的度量。宏观平均度量是通过对所有形状类别的度量进行简单平均来计算的,微观平均度量是通过加权平均来计算的,加权平均的权重与类别中的形状数量成比例。用直方图损失[33]训练的深度15Kd网络用于此任务,具有大小为16的叶子表示(使用附加的乘法层从三个坐标系获得)和大小为32_32_64_64_128_128_256_256_512_512_1024_2048_512的中间表示。
使用获得的大小为512的描述符计算相似度并对每个形状进行预测。从数据集的验证部分获得的结果中选择相似性截断。
一般来说,我们的方法与基于多视图CNN[31]的系统性能相当,并且优于参与SHREC'16的“正常”集合的其他系统。对于“扰动”版本,Kdnetworks的性能受到全局旋转的非不变性的影响。为了解决这个问题,我们实现了一个简单的修改(本着TI-Pooling[14]的精神),该修改将Kd-网络(深度10)应用于模型的20个不同的随机旋转,并对生成的表示执行最大池,然后是三个完全连接的层,以产生最终的形状描述符。所得到的系统在基准的“扰动”版本上获得了有竞争力的性能(表3)。
4.3。零件分割
最后,我们使用了在第3.6节中讨论的架构来预测点云内的各个点的部分标签(例如在飞机中,每个点可以对应于身体、翼、尾部或发动机)。
数据集和数据处理。我们评估我们的架构在SeNeNet部分数据集的部分分割从[ 37 ]。它包含16881个形状,表示为16个类别的单独点云,每个点注释(总共有50个部分)。在该数据集中,类别中的类别和部分都是高度不平衡的,这对包括我们的所有方法都提出了挑战。
培训和测试程序。Since the number of points representing each model differs in the dataset, we upsample each point cloud to size 4196 by duplicating random points with an addition of a small noise. 除了数据为我们的方法是可行的,这样有助于稀有类上。上采样的点云则是美联储在图3所示的结构,这是与平均交叉熵在云的所有点作为损失函数优化。在测试时间的预测是对采用云计算,那么原来云是通过构建KD树获得每个叶索引映射到相应的原始点集。这是进一步用于每一点产生最后的预言。类似于其他的任务,我们使用数据增强系统的培训和测试期间的平均预测多个KD树。
部分分割性能基准。我们的研究结果进行比较,3d-cnn(从[ 20 ]转载),pointnet结构[ 20 ],和[ 37 ]建筑。每个类别均交上联盟(IOU)是一种度量:各种形状的白条是计算每一部分将有可能在这个形状的范畴产生的形状出现白条白条平均超过所有类别的形状,平均。一个深度12变种KD网络用于此任务的大小128,大小128−128−128−256−256−256−256−512−512 512 512 1024−−−中间表示叶表示。另外两个全连接层的尺寸512和1024是用于建筑的瓶颈。分割网络的输出是由三个仿射变换交错热鲁非线性尺寸512, 256, 128进一步处理。这50部分的数据集类中的概率预测(这是不可能的对于一个给定的类被忽略后[ 20 ]协议部分的概率)。批量化应用到每一层的整体架构。
KD网络性能(表4)的部分分割的任务是提高竞争虽然不是最先进的。我们推测,原因之一可能是在KD树在高层分裂信息不足,传播,虽然得到的分割通常不显示潜在的KD树结构的标志(图5)。对于分割任务大KD网络优点是低内存占用。因此,我们的特殊结构,在学习过程中的一个例子的足迹小于120 MB。
5。结论
在这项工作中,我们提出了新的深层学习架构,能够产生适合于不同3D数据识别任务的表示,这些任务直接与点云一起工作。我们的结构与卷积网络有很多相似之处,但是它使用kd-树而不是统一的网格来构建计算图和共享可学习的参数。利用我们的模型,我们在各种识别问题上取得了与当前最新技术相当的结果。与性能最好的卷积结构相比,kd-tree在测试时和训练时也是有效的。
基于kd-tree的深层体系结构的竞争性能表明,其他层次化的3D空间划分结构,如八叉树、PCA树、边界体层次结构等都应该作为深层体系结构的底层结构来研究。
确认:这项工作得到了俄罗斯MES赠款RFMEFI61516X0003的支持。
References
[1] J. L. Bentley. Multidimensional binary search trees used for associative searching. Communications of the ACM,18(9):509–517, 1975.
[2] D. Boscaini, J. Masci, S. Melzi, M. M. Bronstein, U. Castellani, and P. Vandergheynst. Learning class-specific descriptors for deformable shapes using localized spectral convolutional networks. Comput. Graph. Forum, 34(5):13–23, 2015.
[3] D. Boscaini, J. Masci, E. Rodola, and M. M. Bronstein. `Learning shape correspondence with anisotropic convolutional neural networks. In Proc. NIPS, pages 3189–3197,2016.
[4] A. Brock, T. Lim, J. Ritchie, and N. Weston. Generative and discriminative voxel modeling with convolutional neural networks. arXiv preprint arXiv:1608.04236, 2016.
[5] J. Bromley, J. W. Bentz, L. Bottou, I. Guyon, Y. LeCun, C. Moore, E. Sackinger, and R. Shah. Signature verifica- ¨ tion using a siamese time delay neural network. International Journal of Pattern Recognition and Artificial Intelligence, 7(04):669–688, 1993.
[6] J. Bruna, W. Zaremba, A. Szlam, and Y. LeCun. Spectral networks and locally connected networks on graphs. arXiv preprint arXiv:1312.6203, 2013.
[7] A. X. Chang, T. Funkhouser, L. Guibas, P. Hanrahan, Q. Huang, Z. Li, S. Savarese, M. Savva, S. Song, H. Su, et al. Shapenet: An information-rich 3d model repository. arXiv preprint arXiv:1512.03012, 2015.
[8] S. Chopra, R. Hadsell, and Y. LeCun. Learning a similarity metric discriminatively, with application to face verification. In Proc. CVPR, pages 539–546, 2005.
[9] S. Dieleman, J. Schlter, C. Raffel, E. Olson, et al. Lasagne: First release., Aug. 2015.
[10] J. D. Foley, A. Van Dam, S. K. Feiner, J. F. Hughes, and R. L. Phillips. Introduction to computer graphics, volume 55.
Addison-Wesley Reading, 1994.
[11] A. Guttman, M. Stonebraker, and C. U. B. E. R. LAB. Rtrees: A Dynamic Index Structure for Spatial Searching.
Memorandum (University of California, Berkeley, Electronics Research Laboratory). Defense Technical Information
Center, 1983.
[12] V. Hegde and R. Zadeh. Fusionnet: 3d object classification using multiple data representations. arXiv preprint
arXiv:1607.05695, 2016.
[13] M. Jaderberg, K. Simonyan, A. Zisserman, and K. Kavukcuoglu. Spatial transformer networks. In Proc. NIPS, pages 2017–2025, 2015.
[14] D. Laptev, N. Savinov, J. M. Buhmann, and M. Pollefeys. TI-POOLING: transformation-invariant pooling for feature
learning in convolutional neural networks. In Proc. CVPR, pages 289–297, 2016.
[15] Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner. Gradientbased learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.
[16] Y. Li, S. Pirk, H. Su, C. R. Qi, and L. J. Guibas. Fpnn: Field probing neural networks for 3d data. In Proc. NIPS, 2016.
[17] J. Long, E. Shelhamer, and T. Darrell. Fully convolutional networks for semantic segmentation. In Proc. CVPR, pages
3431–3440, 2015.
[18] D. Maturana and S. Scherer. Voxnet: A 3d convolutional neural network for real-time object recognition. In Proc.IROS, pages 922–928. IEEE, 2015.
[19] D. J. Meagher. Octree encoding: A new technique for the representation, manipulation and display of arbitrary 3-d objects by computer. Electrical and Systems Engineering Department Rensseiaer Polytechnic Institute Image Processing Laboratory, 1980.
[20] C. R. Qi, H. Su, K. Mo, and L. J. Guibas. Pointnet: Deep learning on point sets for 3d classification and segmentation.
arXiv preprint arXiv:1612.00593, 2016.
[21] C. R. Qi, H. Su, M. Niessner, A. Dai, M. Yan, and L. J. Guibas. Volumetric and multi-view cnns for object classification on 3d data. In Proc. CVPR, 2016.
[22] A. Requicha, H. Voelcker, and U. of Rochester. Production Automation Project. Constructive Solid Geometry. TM (Rochester, PAP). Production Automation Project, University of Rochester, 1977.
[23] G. Riegler, A. O. Ulusoy, and A. Geiger. Octnet: Learning deep 3d representations at high resolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017.
[24] O. Ronneberger, P. Fischer, and T. Brox. U-net: Convolutional networks for biomedical image segmentation. In Proc. MICCAI, pages 234–241. Springer, 2015.
[25] H. Samet. The design and analysis of spatial data structures, volume 199. Addison-Wesley Reading, MA, 1990.
[26] M. Savva, F. Yu, H. Su, M. Aono, B. Chen, D. Cohen-Or, W. Deng, H. Su, S. Bai, X. Bai, et al. SHREC16 track largescale 3d shape retrieval from ShapeNet Core-55. In Proceedings of the Eurographics Workshop on 3D Object Retrieval, 2016.
[27] M. Schultz and T. Joachims. Learning a distance metric from relative comparisons. Advances in neural information processing systems (NIPS), page 41, 2004.
[28] R. A. Schumacker, B. Brand, M. G. Gilliland, and W. H. Sharp. Study for applying computer-generated images to visual simulation. Technical report, DTIC Document, 1969.
[29] M. Simonovsky and N. Komodakis. Dynamic edgeconditioned filters in convolutional neural networks on graphs. In Proc. CVPR, 2017.
[30] R. Socher, C. C. Lin, C. Manning, and A. Y. Ng. Parsing natural scenes and natural language with recursive neural networks. In Proc. ICML, pages 129–136, 2011.
[31] H. Su, S. Maji, E. Kalogerakis, and E. Learned-Miller. Multiview convolutional neural networks for 3d shape recognition. In Proc. ICCV, pages 945–953, 2015.
[32] Theano Development Team. Theano: A Python framework for fast computation of mathematical expressions. arXiv eprints, abs/1605.02688, May 2016.
[33] E. Ustinova and V. S. Lempitsky. Learning deep embeddings with histogram loss. In Proc. NIPS, pages 4170–4178, 2016.
[34] D. Z. Wang and I. Posner. Voting for voting in online point cloud object detection. In Proc. RSS, 2015.
[35] J. Wu, C. Zhang, T. Xue, B. Freeman, and J. Tenenbaum. Learning a probabilistic latent space of object shapes via 3d generative-adversarial modeling. In Proc. NIPS, pages 82– 90, 2016.
[36] Z. Wu, S. Song, A. Khosla, F. Yu, L. Zhang, X. Tang, and J. Xiao. 3d shapenets: A deep representation for volumetric shapes. In Proc. CVPR, pages 1912–1920, 2015.
[37] L. Yi, V. G. Kim, D. Ceylan, I. Shen, M. Yan, H. Su, A. Lu, Q. Huang, A. Sheffer, L. Guibas, et al. A scalable active framework for region annotation in 3d shape collections. ACM Transactions on Graphics (TOG), 35(6):210, 2016.