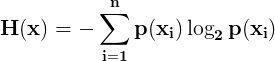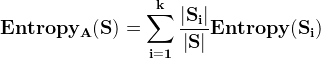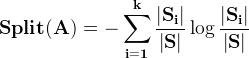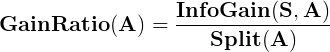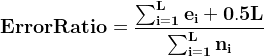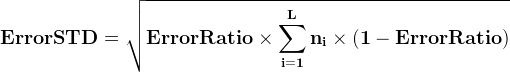机器学习之C4.5算法原理

C4.5算法是由澳大利亚悉尼大学Ross Quinlan教授在1993年基于ID3算法的改进提出的，C4.5 使用信息增益率而不是信息增益作为决策树的属性选择标准。

• 它能够处理连续型属性或离散型属性的数据；
• 能够处理具有缺失值的属性数据；
• 使用信息增益率而不是信息增益作为决策树的属性选择标准；
• 对生成枝剪枝，降低过拟合。

一 、C4.5算法原理介绍

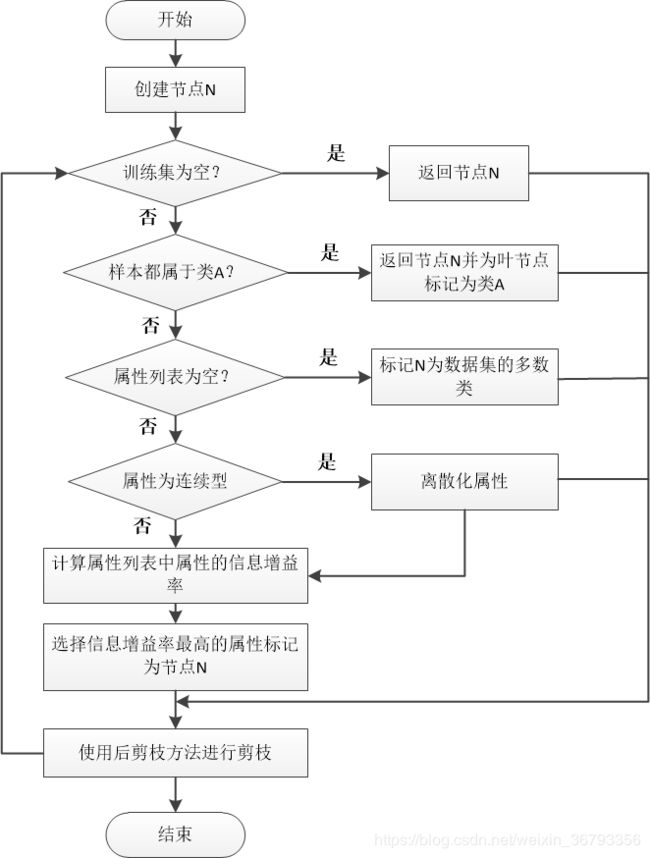
1.C4.5算法流程图

2.信息熵

3.划分信息熵

4.信息增益

5.分裂信息

6.信息增益率

7.剪枝------PEP算法

8.缺失属性值的处理

9.C4.5算法优缺点分析

二、实例分析

1.计算样本的信息熵

2.分别计算不同属性对S的划分信息熵

3.根据Outlook计算信息增益

4.计算分裂信息

5.计算信息增益率

6.选择最大信息增益率的节点

---

一 、C4.5算法原理介绍

1.C4.5算法流程图

                                  

2.信息熵

                            

其中，n表示分类数，p(xi)表示样本xi所占的比例

3.划分信息熵

设选择属性A作为划分数据集S的特征，计算属性A对集合S的划分信息熵值

(1) A为离散类型,根据属性A的k个不同取值将S划分为k各子集{s1,s2, ...,sk}，则属性A划分S的划分信息熵为：

                           

  其中表示Si包含的样本个数占总样本数的比例

(2)A为连续类型，则需要对数据进行离散化处理。

• 首先将属性A的N个属性值按照升序排列，分别使用N-1种二分划分法将属性A的所有属性值分成两部分（二分的阈值为相邻两个属性值的中间值）；
• 然后分别计算N-1种划分方法对应的信息增益；
• 最终选取信息增益最大的二分结果作为对属性A的划分结果，此时的二分阈值作为属性A的二分阈值。

按属性A的取值递增排序，将每对相邻值的中点看作可能的分裂点，对每个可能的分裂点，计算：

                            

其中，和分别对应于该分裂点划分的左右两部分子集，选择值最小的分裂点作为属性A的最佳分裂点，并以该最佳分裂点按属性A对集合S的划分熵值作为属性A划分S的熵值.

4.信息增益

按属性A划分数据集S的信息增益Gain(S,A)为样本集S的熵减去按属性A划分S后的样本子集的熵，即

                         

5.分裂信息

                          

利用引入属性的分裂信息来调节信息增益

6.信息增益率

                         

信息增益率将分裂信息作为分母，属性取值数目越大，分裂信息值越大，从而部分抵消了属性取值数目所带来的影响。相比ID3直接使用信息熵的增益选取最佳属性，避免因某属性有较多分类取值因而有较大的信息熵，从而更容易被选中作为划分属性的情况。通过C4.5算法构造决策树时，信息增益率最大的属性即为当前节点的分裂属性，随着递归计算，被计算的属性的信息增益率会变得越来越小，到后期则选择相对比较大的信息增益率的属性作为分裂属性。

7.剪枝------PEP算法

决策树的建立完全是依赖于训练样本，因此该决策树对训练样本能够产生完美的拟合效果。但这样的决策树对于测试样本来说过于庞大而复杂，可能产生较高的分类错误率。这种现象就称为过拟合。因此需要将复杂的决策树进行简化，即去掉一些节点解决过拟合问题，这个过程称为剪枝。 剪枝方法分为预剪枝和后剪枝两大类。

预剪枝是在构建决策树的过程中（仅用到训练集），设置一个阈值，使得当在当前分裂节点中分裂前和分裂后的误差超过这个阈值则分列，否则不进行分裂操作。它提前终止了决策树的生长，从而避免过多的节点产生。预剪枝方法虽然简单但实用性不强，因为很难精确的判断何时终止树的生长。

后剪枝是在决策树构建完成之后，对那些置信度不达标的节点子树用叶子结点代替，该叶子结点的类标号用该节点子树中频率最高的类标记。后剪枝方法又分为两种，一类是把训练数据集分成树的生长集和剪枝集；另一类算法则是使用同一数据集进行决策树生长和剪枝。常见的后剪枝方法有CCP(Cost Complexity Pruning)、REP(Reduced Error Pruning)、PEP(Pessimistic Error Pruning)、MEP(Minimum Error Pruning)。 

C4.5算法采用PEP(Pessimistic Error Pruning)剪枝法。PEP剪枝法由Quinlan提出，是一种自上而下的剪枝法，根据剪枝前后的错误率来判定是否进行子树的修剪，因此不需要单独的剪枝数据集。 

对于一个叶子节点，它覆盖了n个样本，其中有e个错误，那么该叶子节点的错误率为，其中0.5为惩罚因子（惩罚因子一般取值为0.5）。 对于一棵子树，它有L个叶子节点，那么该子树的误判率为： 

                                 

其中，ei表示子树第i个叶子节点错误分类的样本数量，ni表示表示子树第i个叶子节点中样本的总数量。 

假设一棵子树错误分类一个样本取值为1，正确分类一个样本取值为0，那么子树的误判次数可以认为是一个伯努利分布，因此可以得到该子树误判次数的均值和标准差： 
                                

                                 

把子树替换成叶子节点后，该叶子节点的误判率为： 

                                 

同时，该叶子结点的误判次数也是一个伯努利分布，因此该叶子节点误判次数的均值为： 

                                 

剪枝的条件为：

                                 

满足剪枝条件时，则将所得叶子节点替换该子树，即为剪枝操作。

8.缺失属性值的处理

训练样本集中有可能会出现一些样本缺失了一些属性值，待分类样本中也可能会出现这样的情况。含有缺失属性的样本集会一般会导致三个问题： 

  （１）在构建决策树时，每一个分裂属性的选取是由训练样本集中所有属性的信息増益率来决定的。而在此阶段，如果训练样本集中有些样本缺少一部分属性，此时该如何计算该属性的信息増益率； 
  （２）当已经选择某属性作为分裂属性时，样本集应该根据该属性的值来进行分支，但对于那些该属性的值为未知的样本，应该将它分支到哪一棵子树上； 
  （３）在决策树已经构建完成后，如果待分类样本中有些属性值缺失，则该样本的分类过程如何进行。 

  针对上述因缺失属性值引起的三个问题，C4.5算法有多种解决方案。

  （1）针对问题一，在计算各属性的信息増益率时，若某些样本的属性值未知，有两种处理方式：

                      ① 计算某属性的信息増益率时忽略掉缺失了此属性的样本；

                      ② 通过此属性的样本中出现频率最高的属性值，賦值给缺失了此属性的样本。 

  （2）针对问题二，假设属性Ａ已被选择作为决策树中的一个分支节点，在对样本集进行分支的时候，对于那些属性Ａ的值未知的样本，有三种处理方式：

                ① 不处理那些属性Ａ未知的样本，即简单的忽略它们；

                ② 根据属性Ａ的其他样本的取值，来对未知样本进行赋值；

                ③ 为缺失属性Ａ的样本单独创建一个分支，不过这种方式得到的决策树模型结点数显然要増加，使模型更加复杂了。

  （3）针对问题三，根据己经生成的决策树模型，对一个待分类的样本进行分类时，若此样本的属性Ａ的值未知，有两种处理方式：

               ① 待分类样本在到达属性Ａ的分支结点时即可结束分类过程，此样本所属类别为属性Ａ的子树中概率最大的类别；

               ② 把待分类样本的属性Ａ赋予一个最常见的值，然后继续分类过程。

9.C4.5算法优缺点分析

优点： 
（1）通过信息增益率选择分裂属性，克服了ID3算法中通过信息增益倾向于选择拥有多个属性值的属性作为分裂属性的不足； 
（2）能够处理离散型和连续型的属性类型，即将连续型的属性进行离散化处理； 
（3）构造决策树之后进行剪枝操作； 
（4）能够处理具有缺失属性值的训练数据。
缺点： 
（1）算法的计算效率较低，特别是针对含有连续属性值的训练样本时表现的尤为突出。 
（2）算法在选择分裂属性时没有考虑到条件属性间的相关性，只计算数据集中每一个条件属性与决策属性之间的期望信息，有可能影响到属性选择的正确性。

二、实例分析

                        

1.计算样本的信息熵

                  

2.分别计算不同属性对S的划分信息熵

          A = Outlook

          

          

3.根据Outlook计算信息增益

         

4.计算分裂信息

         

5.计算信息增益率

         

6.选择最大信息增益率的节点

重复1-5步分别计算Temperature、Humidty、Windy的信息增益率

        

        

        

对比可知，Outlook属性对应的信息增益率最大，一次选择Outlook属性作为根节点

参考原文：https://blog.csdn.net/zhihua_oba/article/details/70632622 
参考原文：http://blog.csdn.net/u010498696/article/details/46333911