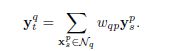超分辨率重建经典方法——Super-Resolution Through Neighbor Embedding
超分辨率重建之—NE
论文笔记:
摘要
该算法受到了最近的(manifold learning)流行学习算法的启发,特别是局部线性嵌入(LLE)。我们运用局部重叠来增强重建高分图像块之间的兼容性和平滑约束。具体来说,高分和低分图像块在两个不同的特征空间中形成了类似局部几何的流形。就像LLE中,局部几何结构特征是通过 一个块(patch)的特征向量在特征空间如何被邻域重构 而形成的。除了用训练的图像对来估计高分的嵌入(embedding),我们还通过重叠方法在高分图像上实施了块之间的局部兼容性和平滑约束。实验结果显示效果很好。
基础不好的(比如我)会有疑问就是“流行学习”和“局部嵌入式”是什么?
参考:http://blog.csdn.net/chl033/article/details/6107042
流形学习(manifold learning)
假设数据是均匀采样于一个高维欧氏空间中的低维流形,流形学习就是从高维采样数据中恢复低维流形结构,即找到高维空间中的低维流形,并求出相应的嵌入映射,以实现维数约简或者数据可视化。简单说,它是从观测到的现象中去寻找事物的本质,找到产生数据的内在规律。流形学习方法是模式识别中的基本方法,分为线性流形学习算法和非线性流形学习算法,线性方法就是传统的方法如主成分分析(PCA)和线性判别分析(LDA),非线行流形学习算法包括等距映射(Isomap),拉普拉斯特征映射(LE)等。
流形学习是个很广泛的概念。自从2000年以后,流形学习被认为属于非线性降维的一个分支。众所周知,引导这一领域迅速发展的是2000年Science杂志上的两篇文章: Isomap and LLE (Locally Linear Embedding)。
流形学习的基本概念
所谓流形(manifold)就是一般的几何对象的总称。流形就包括各种维数的曲线曲面等。和一般的降维分析一样,流形学习把一组在高维空间中的数据在低维空间中重新表示。和以往方法不同的是,在流形学习中有一个假设,就是所处理的数据采样于一个潜在的流形上,或是说对于这组数据存在一个潜在的流形。对于不同的方法,对于流形性质的要求各不相同,这也就产生了在流形假设下的各种不同性质的假设。
局部嵌入式 LLE (Locally linear Embedding)
LLE的思想就是,一个流形在很小的局部邻域上可以近似看成欧式的,就是局部线性的。那么,在小的局部邻域上,一个点就可以用它周围的点在最小二乘意义下最优的线性表示。LLE把这个线性拟合的系数当成这个流形局部几何性质的刻画。那么一个好的低维表示,就应该也具有同样的局部几何,所以利用同样的线性表示的表达式,最终写成一个二次型的形式,十分自然优美。
注意在LLE出现的两个加和优化的线性表达,第一个是求每一点的线性表示系数的。虽然原始公式中是写在一起的,但是求解时,是对每一个点分别来求得。第二个表示式,是已知所有点的线性表示系数,来求低维表示(或嵌入embedding)的,他是一个整体求解的过程。
正文:
单张图像超分重建问题的解决可以被阐述成:我们输入低分影像,通过对一系列高低分影像对的学习,来生成重建后的高分影像。
每一个高分图像块的生成不仅和相对应的低分图像块有关,还和相邻的高分图像快有关。前者决定准确性,后者决定局部兼容性和平滑性。为了满足以上设想,我们算法具有三个属性:
(1) 每一个高分块都与多个转化方式(训练集中学习来的)相对应;
(2) 局部低分块之间的关系应该在高分集中体现出来;
(3) 高分集中的相邻块通过重叠约束来增强局部的兼容性和平滑性。
流形学习
我们的算法基于假设:高分、低分图像的块在两个独特的特征空间里形成了相同几何结构的流形。
LLE总结如下:
(1) 对于每一个在D维空间的数据点:
a. 找到在相同空间一些最邻近的邻域值;
b. 计算邻域值的重建权重,使重建误差最小
(2) 在d维的嵌入空间计算计算低维嵌入值,依靠重建权重表达能够很好保存局部结构的低维嵌入。
我们的NE算法
(1) 首先,对于低分图像的每一个块Xt,计算在Xs中邻近值的重建权重使得重建误差最小。
(2) 用保存局部结构的训练的图像对来估算高分嵌入值。
(3) 通过邻近块的叠加来形成高分影像,保持局部兼容性和平滑。
1. 每一个patch 表示为x(q,t)在图像Xt中:
a.在Xs中找到K个邻域值形成集合Nq
b.计算领域值的重建系数,使得重建x(q,t)误差最小
c.用合适的K个邻域值相关的高分特征和重建系数,来计算高分嵌入值y(q,t)
2. 对1(c)中得到的相邻块进行局部的兼容性和平滑处理得到最终的高分影像。
其中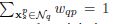
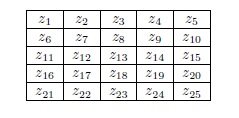
第二步,取相邻patch重叠部分的平均值。
特征表达
对于低分图像,用(亮度的)一阶和二阶梯度提取特征:
5X5邻域特征提取
对于高分图像,每个高分块减去均值作为特征。当重建时,对应的低分块亮度均值被加上。
数据集和参数
数据集采用高分影像,低分是高分降采样。
训练集很小,每个块用八个不同的特征向量表示,通过不同的方向(0,90,180,270)可以通过镜像图像增加训练数据量。
我们的方法只有三个参数:K=5,patch大小为3X3,放大N呗高分图像用3NX3N。
(a)高分原图
(b)对应的降采样低分图
(c)是(b)的五个邻域
(d)是(c)对应的五个高分图
(e)为重建结果,和(a)相近
证明方法效果很好
论文笔记:
摘要
该算法受到了最近的(manifold learning)流行学习算法的启发,特别是局部线性嵌入(LLE)。我们运用局部重叠来增强重建高分图像块之间的兼容性和平滑约束。具体来说,高分和低分图像块在两个不同的特征空间中形成了类似局部几何的流形。就像LLE中,局部几何结构特征是通过 一个块(patch)的特征向量在特征空间如何被邻域重构 而形成的。除了用训练的图像对来估计高分的嵌入(embedding),我们还通过重叠方法在高分图像上实施了块之间的局部兼容性和平滑约束。实验结果显示效果很好。
基础不好的(比如我)会有疑问就是“流行学习”和“局部嵌入式”是什么?
参考:http://blog.csdn.net/chl033/article/details/6107042
流形学习(manifold learning)
假设数据是均匀采样于一个高维欧氏空间中的低维流形,流形学习就是从高维采样数据中恢复低维流形结构,即找到高维空间中的低维流形,并求出相应的嵌入映射,以实现维数约简或者数据可视化。简单说,它是从观测到的现象中去寻找事物的本质,找到产生数据的内在规律。流形学习方法是模式识别中的基本方法,分为线性流形学习算法和非线性流形学习算法,线性方法就是传统的方法如主成分分析(PCA)和线性判别分析(LDA),非线行流形学习算法包括等距映射(Isomap),拉普拉斯特征映射(LE)等。
流形学习是个很广泛的概念。自从2000年以后,流形学习被认为属于非线性降维的一个分支。众所周知,引导这一领域迅速发展的是2000年Science杂志上的两篇文章: Isomap and LLE (Locally Linear Embedding)。
流形学习的基本概念
所谓流形(manifold)就是一般的几何对象的总称。流形就包括各种维数的曲线曲面等。和一般的降维分析一样,流形学习把一组在高维空间中的数据在低维空间中重新表示。和以往方法不同的是,在流形学习中有一个假设,就是所处理的数据采样于一个潜在的流形上,或是说对于这组数据存在一个潜在的流形。对于不同的方法,对于流形性质的要求各不相同,这也就产生了在流形假设下的各种不同性质的假设。
局部嵌入式 LLE (Locally linear Embedding)
LLE的思想就是,一个流形在很小的局部邻域上可以近似看成欧式的,就是局部线性的。那么,在小的局部邻域上,一个点就可以用它周围的点在最小二乘意义下最优的线性表示。LLE把这个线性拟合的系数当成这个流形局部几何性质的刻画。那么一个好的低维表示,就应该也具有同样的局部几何,所以利用同样的线性表示的表达式,最终写成一个二次型的形式,十分自然优美。
注意在LLE出现的两个加和优化的线性表达,第一个是求每一点的线性表示系数的。虽然原始公式中是写在一起的,但是求解时,是对每一个点分别来求得。第二个表示式,是已知所有点的线性表示系数,来求低维表示(或嵌入embedding)的,他是一个整体求解的过程。
正文:
单张图像超分重建问题的解决可以被阐述成:我们输入低分影像,通过对一系列高低分影像对的学习,来生成重建后的高分影像。
每一个高分图像块的生成不仅和相对应的低分图像块有关,还和相邻的高分图像快有关。前者决定准确性,后者决定局部兼容性和平滑性。为了满足以上设想,我们算法具有三个属性:
(1) 每一个高分块都与多个转化方式(训练集中学习来的)相对应;
(2) 局部低分块之间的关系应该在高分集中体现出来;
(3) 高分集中的相邻块通过重叠约束来增强局部的兼容性和平滑性。
流形学习
我们的算法基于假设:高分、低分图像的块在两个独特的特征空间里形成了相同几何结构的流形。
LLE总结如下:
(1) 对于每一个在D维空间的数据点:
a. 找到在相同空间一些最邻近的邻域值;
b. 计算邻域值的重建权重,使重建误差最小
(2) 在d维的嵌入空间计算计算低维嵌入值,依靠重建权重表达能够很好保存局部结构的低维嵌入。
我们的NE算法
(1) 首先,对于低分图像的每一个块Xt,计算在Xs中邻近值的重建权重使得重建误差最小。
(2) 用保存局部结构的训练的图像对来估算高分嵌入值。
(3) 通过邻近块的叠加来形成高分影像,保持局部兼容性和平滑。
1. 每一个patch 表示为x(q,t)在图像Xt中:
a.在Xs中找到K个邻域值形成集合Nq
b.计算领域值的重建系数,使得重建x(q,t)误差最小
c.用合适的K个邻域值相关的高分特征和重建系数,来计算高分嵌入值y(q,t)
2. 对1(c)中得到的相邻块进行局部的兼容性和平滑处理得到最终的高分影像。
第一步(a)用欧氏距离来定义邻域。1(b)中找到Xt中的每一个patch x(q,t)中最好的重建系数。最小化局部重建误差得到最佳重建系数:
其中
第一步(c),计算初始y(q,t),基于:
第二步,取相邻patch重叠部分的平均值。
特征表达
对于低分图像,用(亮度的)一阶和二阶梯度提取特征:
5X5邻域特征提取
对于高分图像,每个高分块减去均值作为特征。当重建时,对应的低分块亮度均值被加上。
数据集和参数
数据集采用高分影像,低分是高分降采样。
训练集很小,每个块用八个不同的特征向量表示,通过不同的方向(0,90,180,270)可以通过镜像图像增加训练数据量。
我们的方法只有三个参数:K=5,patch大小为3X3,放大N呗高分图像用3NX3N。
例子展示
(a)高分原图
(b)对应的降采样低分图
(c)是(b)的五个邻域
(d)是(c)对应的五个高分图
(e)为重建结果,和(a)相近
证明方法效果很好

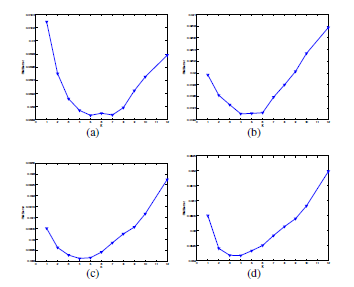
改变K值计算RMS,结果显示,当K=4,5效果最好
引用:Chang H, Yeung D Y, Xiong Y. Super-resolution through neighbor embedding[C]//Computer Vision and Pattern Recognition, 2004. CVPR 2004. Proceedings of the 2004 IEEE Computer Society Conference on. IEEE, 2004, 1: I-I.