[生成对抗网络GAN入门指南](3)GAN的工程实践及基础代码
1、导入相关包,设置随机参数
2、设置真实数据的分布、生成器的初始化分布
3、设置线性运算:并用于生成器和判别器
4、设置优化器,使用学习率衰减的梯度下降方法
5、搭建GAN模型
6、运行主程序
完整代码请直接链接到最后面
从上一章[生成对抗网络GAN入门指南](2)理解生成对抗网络最后,我们需要做的优化是以下这个式子:
上式中期望可以等价于计算真实分布和生成数据分布的积分,在上一章已经完整证明过。
现在我们在前置的随机分布![]() 中取出m个随机数,然后从真实数据
中取出m个随机数,然后从真实数据![]() 中取出m个真实样本,然后使用平均数代替上面的期望。公式改写如下:
中取出m个真实样本,然后使用平均数代替上面的期望。公式改写如下:
伪代码如下:
for训练的迭代次数do
for重复k次do
从生成器的前置随机分布![]() 中取出m个小批次样本;
中取出m个小批次样本;
从真实数据分布![]() 中取出m个小批次样本;
中取出m个小批次样本;
使用随机梯度下降参数:
end for
从生成器前置随机分布![]() 取出m个小批次样本;
取出m个小批次样本;
使用随机梯度下降更新参数;
end for
下面为随机生成的真实高斯分布数据,并用GAN来生成数据。
1、导入相关包,设置随机参数
import argparse
import numpy as np
from scipy.stats import norm
import tensorflow as tf
import matplotlib.pyplot as plt
from matplotlib import animation
import seaborn as sns
sns.set(color_codes=True)
seed = 42
np.random.seed(seed)
tf.set_random_seed(seed)2、设置真实数据的分布、生成器的初始化分布
# 均值为3,方差为0.5的高斯分布
class DataDistribution(object):
def __init__(self):
self.mu = 3
self.sigma = 0.5
def sample(self, N):
samples = np.random.normal(self.mu, self.sigma, N)
samples.sort()
return samples
# 生成器初始分布为平均分布
class GeneratorDistribution(object):
def __init__(self, range):
self.range = range
def sample(self, N):
return np.linspace(-self.range, self.range, N) + \
np.random.random(N) * 0.013、设置线性运算:并用于生成器和判别器
def linear(input, output_dim, scope=None, stddev=1.0):
norm = tf.random_normal_initializer(stddev=stddev)
const = tf.constant_initializer(0.0)
with tf.variable_scope(scope or 'linear'):
w = tf.get_variable('w', [input.get_shape()[1], output_dim], initializer=norm)
b = tf.get_variable('b', [output_dim], initializer=const)
return tf.matmul(input, w) + b
def generator(input, h_dim):
h0 = tf.nn.softplus(linear(input, h_dim, 'g0'))
h1 = linear(h0, 1, 'g1')
return h1
def discriminator(input, h_dim):
h0 = tf.tanh(linear(input, h_dim * 2, 'd0'))
h1 = tf.tanh(linear(h0, h_dim * 2, 'd1'))
h2 = tf.tanh(linear(h1, h_dim * 2, 'd2'))
h3 = tf.sigmoid(linear(h2, 1, 'd3'))
return h34、设置优化器,使用学习率衰减的梯度下降方法
def optimizer(loss, var_list, initial_learning_rate):
decay = 0.95
num_decay_steps = 150
batch = tf.Variable(0)
learning_rate = tf.train.exponential_decay(
initial_learning_rate,
batch,
num_decay_steps,
decay,
staircase=True
)
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(
loss,
global_step=batch,
var_list=var_list
)
return optimizer5、搭建GAN模型
class GAN(object):
def __init__(self, data, gen, num_steps, batch_size, log_every):
self.data = data
self.gen = gen
self.num_steps = num_steps
self.batch_size = batch_size
self.log_every = log_every
self.mlp_hidden_size = 4
self.learning_rate = 0.03
self._create_model()
def _create_model(self):
......
def train(self):
......①创建模型:创建预训练判别器D_pre、生成器Generator和判别器Discriminator
- 创建预训练判别器D_pre
def _create_model(self):
with tf.variable_scope('D_pre'):
self.pre_input = tf.placeholder(tf.float32, shape=(self.batch_size, 1))
self.pre_labels = tf.placeholder(tf.float32, shape=(self.batch_size, 1))
D_pre = discriminator(self.pre_input, self.mlp_hidden_size)
self.pre_loss = tf.reduce_mean(tf.square(D_pre - self.pre_labels))
self.pre_opt = optimizer(self.pre_loss, None, self.learning_rate)- 创建生成器Generator
# This defines the generator network - it takes samples from a noise
# distribution as input, and passes them through an MLP.
with tf.variable_scope('Generator'):
self.z = tf.placeholder(tf.float32, shape=(self.batch_size, 1))
self.G = generator(self.z, self.mlp_hidden_size)- 创建判别器Discriminator
# The discriminator tries to tell the difference between samples from the
# true data distribution (self.x) and the generated samples (self.z).
#
# Here we create two copies of the discriminator network (that share parameters),
# as you cannot use the same network with different inputs in TensorFlow.
with tf.variable_scope('Discriminator') as scope:
self.x = tf.placeholder(tf.float32, shape=(self.batch_size, 1))
self.D1 = discriminator(self.x, self.mlp_hidden_size)
scope.reuse_variables()
self.D2 = discriminator(self.G, self.mlp_hidden_size)- 分别计算生成器和判别器的损失loss_g和loss_d,并进行优化
# Define the loss for discriminator and generator networks (see the original
# paper for details), and create optimizers for both
self.loss_d = tf.reduce_mean(-tf.log(self.D1) - tf.log(1 - self.D2))
self.loss_g = tf.reduce_mean(-tf.log(self.D2))
self.d_pre_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='D_pre')
self.d_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='Discriminator')
self.g_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='Generator')
self.opt_d = optimizer(self.loss_d, self.d_params, self.learning_rate)
self.opt_g = optimizer(self.loss_g, self.g_params, self.learning_rate)②进行训练:预训练判别器D_pre,然后将训练后的参数共享给判别器Discriminator
- 预训练判别器D_pre
def train(self):
with tf.Session() as session:
tf.global_variables_initializer().run()
# pretraining discriminator
num_pretrain_steps = 1000
for step in range(num_pretrain_steps):
d = (np.random.random(self.batch_size) - 0.5) * 10.0
labels = norm.pdf(d, loc=self.data.mu, scale=self.data.sigma)
pretrain_loss, _ = session.run([self.pre_loss, self.pre_opt], {
self.pre_input: np.reshape(d, (self.batch_size, 1)),
self.pre_labels: np.reshape(labels, (self.batch_size, 1))
})
self.weightsD = session.run(self.d_pre_params)
# copy weights from pre-training over to new D network
for i, v in enumerate(self.d_params):
session.run(v.assign(self.weightsD[i]))
for step in range(self.num_steps):
# update discriminator
x = self.data.sample(self.batch_size)
z = self.gen.sample(self.batch_size)
loss_d, _ = session.run([self.loss_d, self.opt_d], {
self.x: np.reshape(x, (self.batch_size, 1)),
self.z: np.reshape(z, (self.batch_size, 1))
})- 将训练后的参数共享给判别器Discriminator
# update generator
z = self.gen.sample(self.batch_size)
loss_g, _ = session.run([self.loss_g, self.opt_g], {
self.z: np.reshape(z, (self.batch_size, 1))
})
if step % self.log_every == 0:
print('{}: {}\t{}'.format(step, loss_d, loss_g))
if step % 100 == 0 or step==0 or step == self.num_steps -1 :
self._plot_distributions(session)③可视化:使用采样展示生成数据和真实数据的分布
- 采样
def _samples(self, session, num_points=10000, num_bins=100):
xs = np.linspace(-self.gen.range, self.gen.range, num_points)
bins = np.linspace(-self.gen.range, self.gen.range, num_bins)
# data distribution
d = self.data.sample(num_points)
pd, _ = np.histogram(d, bins=bins, density=True)
# generated samples
zs = np.linspace(-self.gen.range, self.gen.range, num_points)
g = np.zeros((num_points, 1))
for i in range(num_points // self.batch_size):
g[self.batch_size * i:self.batch_size * (i + 1)] = session.run(self.G, {
self.z: np.reshape(
zs[self.batch_size * i:self.batch_size * (i + 1)],
(self.batch_size, 1)
)
})
pg, _ = np.histogram(g, bins=bins, density=True)
return pd, pg- 可视化
def _plot_distributions(self, session):
pd, pg = self._samples(session)
p_x = np.linspace(-self.gen.range, self.gen.range, len(pd))
f, ax = plt.subplots(1)
ax.set_ylim(0, 1)
plt.plot(p_x, pd, label='Real Data')
plt.plot(p_x, pg, label='Generated Data')
plt.title('GAN Visualization')
plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.legend()
plt.show()6、运行主程序
def main(args):
model = GAN(
DataDistribution(),
GeneratorDistribution(range=8),
args.num_steps,
args.batch_size,
args.log_every,
)
model.train()
def parse_args():
parser = argparse.ArgumentParser()
parser.add_argument('--num-steps', type=int, default=1200,
help='the number of training steps to take')
parser.add_argument('--batch-size', type=int, default=12,
help='the batch size')
parser.add_argument('--log-every', type=int, default=10,
help='print loss after this many steps')
parses = parser.parse_args(args=[])#添加args=[]
return parses注意这里parses = parser.parse_args(args=[])#添加args=[]
如果不加args=[]会报错An exception has occurred, use %tb to see the full traceback.
if __name__ == '__main__':
main(parse_args())结果如下:
0: 0.9058498740196228 3.01792526245117210: 0.3661727011203766 2.4829494953155518
20: 0.2567436695098877 2.527153730392456
30: 0.23893599212169647 2.646153688430786
40: 0.21188394725322723 2.755629301071167
50: 0.24596953392028809 2.7865734100341797
60: 0.27803653478622437 2.819697618484497
70: 0.20561213791370392 3.014293670654297
80: 0.20861400663852692 3.093595266342163
90: 0.1999121755361557 3.1188929080963135
100: 0.8676349520683289 3.1559784412384033110: 0.2710826098918915 3.0497334003448486
120: 0.2979937791824341 3.3270256519317627
130: 0.35235917568206787 3.153003454208374
140: 0.3312816917896271 3.266500234603882
150: 0.44445013999938965 3.2211639881134033
160: 0.830064594745636 2.5850722789764404
170: 1.0792583227157593 2.844705581665039
180: 1.1153842210769653 2.539602279663086
190: 0.9280094504356384 2.582491636276245
200: 0.8895644545555115 2.544771909713745210: 0.8804630637168884 2.5786397457122803
220: 0.9524447321891785 2.5626392364501953
230: 1.0161170959472656 2.6068341732025146
240: 0.9398650527000427 2.61761474609375
250: 0.9690361022949219 2.6562836170196533
260: 0.9535879492759705 2.702772855758667
270: 0.9497044682502747 2.729496955871582
280: 0.9505455493927002 2.7817916870117188
290: 0.9766985774040222 2.822368860244751
300: 0.9790706634521484 2.848435640335083310: 0.9584127068519592 2.831235885620117
320: 0.9558747410774231 2.838682174682617
330: 0.9572162628173828 2.843243360519409
340: 0.9545037150382996 2.8567473888397217
350: 0.9616591930389404 2.8660755157470703
360: 0.9513992667198181 2.8865842819213867
370: 0.9513044953346252 2.8945209980010986
380: 0.9510054588317871 2.9008471965789795
390: 0.9619631767272949 2.911766767501831
400: 0.9593977332115173 2.9199936389923096410: 0.9573793411254883 2.925779104232788
420: 0.9600151181221008 2.9308977127075195
430: 0.9554762840270996 2.9343574047088623
440: 0.9505661129951477 2.9468088150024414
450: 0.9538960456848145 2.9457263946533203
460: 0.9585859179496765 2.964500665664673
470: 0.9657346606254578 2.969087600708008
480: 0.9562466740608215 2.97055721282959
490: 0.9631298184394836 2.9682061672210693
500: 0.9579052925109863 2.98766827583313510: 0.9529304504394531 2.9976375102996826
520: 0.9577788710594177 2.9855854511260986
530: 0.9556493759155273 2.9906623363494873
540: 0.963697612285614 3.0012834072113037
550: 0.9546659588813782 3.0135772228240967
560: 0.954541027545929 3.000689744949341
570: 0.9527294635772705 3.018080949783325
580: 0.9562703967094421 3.0316765308380127
590: 0.9562308192253113 3.033099889755249
600: 0.9676775932312012 3.0354459285736084610: 0.9556455612182617 3.026475667953491
620: 0.9621879458427429 3.0372326374053955
630: 0.9544457793235779 3.041356325149536
640: 0.9505367279052734 3.058652877807617
650: 0.9726033210754395 3.0442416667938232
660: 0.960233747959137 3.048086166381836
670: 0.9602031111717224 3.0599300861358643
680: 0.9553996920585632 3.0656583309173584
690: 0.95340496301651 3.061668634414673
700: 0.9558480381965637 3.0625126361846924710: 0.9548101425170898 3.0637643337249756
720: 0.9591142535209656 3.0792343616485596
730: 0.9580585360527039 3.076420545578003
740: 0.9542174339294434 3.084198236465454
750: 0.9520791172981262 3.0760724544525146
760: 0.9857081770896912 3.0916473865509033
770: 0.954762876033783 3.098372220993042
780: 0.956782341003418 3.101635694503784
790: 0.9556240439414978 3.0913455486297607
800: 0.9452716708183289 3.0873405933380127810: 0.9598703384399414 3.0957539081573486
820: 0.9495179057121277 3.1218841075897217
830: 0.9676353335380554 3.1136913299560547
840: 0.9608518481254578 3.0985374450683594
850: 0.9497320055961609 3.1004221439361572
860: 0.9583330750465393 3.10925030708313
870: 0.9575583338737488 3.115415573120117
880: 0.9481444954872131 3.142063856124878
890: 0.9595341086387634 3.1321611404418945
900: 0.9526324272155762 3.115969657897949910: 0.957833468914032 3.1158668994903564
920: 0.9581219553947449 3.13159441947937
930: 0.9586291313171387 3.1408939361572266
940: 0.9535805583000183 3.152231454849243
950: 0.9539173245429993 3.1291332244873047
960: 0.9537625312805176 3.130748748779297
970: 0.9528759121894836 3.1425857543945312
980: 0.9532210230827332 3.150545835494995
990: 0.9515659213066101 3.157489776611328
1000: 0.9518685936927795 3.1409137248992921010: 0.9496883749961853 3.143315315246582
1020: 0.9560754895210266 3.156165361404419
1030: 0.9554839134216309 3.1636600494384766
1040: 0.9747700095176697 3.1666743755340576
1050: 0.9559829235076904 3.1536171436309814
1060: 0.9466338753700256 3.153604507446289
1070: 0.9512701034545898 3.1573095321655273
1080: 0.9531095623970032 3.1709377765655518
1090: 0.9690462946891785 3.1741015911102295
1100: 0.9565709233283997 3.1730530261993411110: 0.9528694748878479 3.1647026538848877
1120: 0.9897692799568176 3.173391342163086
1130: 0.9538822770118713 3.1752426624298096
1140: 0.9539585709571838 3.1887900829315186
1150: 0.9726629257202148 3.1818549633026123
1160: 0.9535603523254395 3.177844285964966
1170: 0.9504902958869934 3.1759109497070312
1180: 0.9564926028251648 3.1849753856658936
1190: 0.9527941346168518 3.2040793895721436完整代码
import argparse
import numpy as np
from scipy.stats import norm
import tensorflow as tf
import matplotlib.pyplot as plt
from matplotlib import animation
import seaborn as sns
sns.set(color_codes=True)
seed = 42
np.random.seed(seed)
tf.set_random_seed(seed)
class DataDistribution(object):
def __init__(self):
self.mu = 3
self.sigma = 0.5
def sample(self, N):
samples = np.random.normal(self.mu, self.sigma, N)
samples.sort()
return samples
class GeneratorDistribution(object):
def __init__(self, range):
self.range = range
def sample(self, N):
return np.linspace(-self.range, self.range, N) + \
np.random.random(N) * 0.01
def linear(input, output_dim, scope=None, stddev=1.0):
norm = tf.random_normal_initializer(stddev=stddev)
const = tf.constant_initializer(0.0)
with tf.variable_scope(scope or 'linear'):
w = tf.get_variable('w', [input.get_shape()[1], output_dim], initializer=norm)
b = tf.get_variable('b', [output_dim], initializer=const)
return tf.matmul(input, w) + b
def generator(input, h_dim):
h0 = tf.nn.softplus(linear(input, h_dim, 'g0'))
h1 = linear(h0, 1, 'g1')
return h1
def discriminator(input, h_dim):
h0 = tf.tanh(linear(input, h_dim * 2, 'd0'))
h1 = tf.tanh(linear(h0, h_dim * 2, 'd1'))
h2 = tf.tanh(linear(h1, h_dim * 2, 'd2'))
h3 = tf.sigmoid(linear(h2, 1, 'd3'))
return h3
def optimizer(loss, var_list, initial_learning_rate):
decay = 0.95
num_decay_steps = 150
batch = tf.Variable(0)
learning_rate = tf.train.exponential_decay(
initial_learning_rate,
batch,
num_decay_steps,
decay,
staircase=True
)
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(
loss,
global_step=batch,
var_list=var_list
)
return optimizer
class GAN(object):
def __init__(self, data, gen, num_steps, batch_size, log_every):
self.data = data
self.gen = gen
self.num_steps = num_steps
self.batch_size = batch_size
self.log_every = log_every
self.mlp_hidden_size = 4
self.learning_rate = 0.03
self._create_model()
def _create_model(self):
with tf.variable_scope('D_pre'):
self.pre_input = tf.placeholder(tf.float32, shape=(self.batch_size, 1))
self.pre_labels = tf.placeholder(tf.float32, shape=(self.batch_size, 1))
D_pre = discriminator(self.pre_input, self.mlp_hidden_size)
self.pre_loss = tf.reduce_mean(tf.square(D_pre - self.pre_labels))
self.pre_opt = optimizer(self.pre_loss, None, self.learning_rate)
# This defines the generator network - it takes samples from a noise
# distribution as input, and passes them through an MLP.
with tf.variable_scope('Generator'):
self.z = tf.placeholder(tf.float32, shape=(self.batch_size, 1))
self.G = generator(self.z, self.mlp_hidden_size)
# The discriminator tries to tell the difference between samples from the
# true data distribution (self.x) and the generated samples (self.z).
#
# Here we create two copies of the discriminator network (that share parameters),
# as you cannot use the same network with different inputs in TensorFlow.
with tf.variable_scope('Discriminator') as scope:
self.x = tf.placeholder(tf.float32, shape=(self.batch_size, 1))
self.D1 = discriminator(self.x, self.mlp_hidden_size)
scope.reuse_variables()
self.D2 = discriminator(self.G, self.mlp_hidden_size)
# Define the loss for discriminator and generator networks (see the original
# paper for details), and create optimizers for both
self.loss_d = tf.reduce_mean(-tf.log(self.D1) - tf.log(1 - self.D2))
self.loss_g = tf.reduce_mean(-tf.log(self.D2))
self.d_pre_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='D_pre')
self.d_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='Discriminator')
self.g_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='Generator')
self.opt_d = optimizer(self.loss_d, self.d_params, self.learning_rate)
self.opt_g = optimizer(self.loss_g, self.g_params, self.learning_rate)
def train(self):
with tf.Session() as session:
tf.global_variables_initializer().run()
# pretraining discriminator
num_pretrain_steps = 1000
for step in range(num_pretrain_steps):
d = (np.random.random(self.batch_size) - 0.5) * 10.0
labels = norm.pdf(d, loc=self.data.mu, scale=self.data.sigma)
pretrain_loss, _ = session.run([self.pre_loss, self.pre_opt], {
self.pre_input: np.reshape(d, (self.batch_size, 1)),
self.pre_labels: np.reshape(labels, (self.batch_size, 1))
})
self.weightsD = session.run(self.d_pre_params)
# copy weights from pre-training over to new D network
for i, v in enumerate(self.d_params):
session.run(v.assign(self.weightsD[i]))
for step in range(self.num_steps):
# update discriminator
x = self.data.sample(self.batch_size)
z = self.gen.sample(self.batch_size)
loss_d, _ = session.run([self.loss_d, self.opt_d], {
self.x: np.reshape(x, (self.batch_size, 1)),
self.z: np.reshape(z, (self.batch_size, 1))
})
# update generator
z = self.gen.sample(self.batch_size)
loss_g, _ = session.run([self.loss_g, self.opt_g], {
self.z: np.reshape(z, (self.batch_size, 1))
})
if step % self.log_every == 0:
print('{}: {}\t{}'.format(step, loss_d, loss_g))
if step % 100 == 0 or step==0 or step == self.num_steps -1 :
self._plot_distributions(session)
def _samples(self, session, num_points=10000, num_bins=100):
xs = np.linspace(-self.gen.range, self.gen.range, num_points)
bins = np.linspace(-self.gen.range, self.gen.range, num_bins)
# data distribution
d = self.data.sample(num_points)
pd, _ = np.histogram(d, bins=bins, density=True)
# generated samples
zs = np.linspace(-self.gen.range, self.gen.range, num_points)
g = np.zeros((num_points, 1))
for i in range(num_points // self.batch_size):
g[self.batch_size * i:self.batch_size * (i + 1)] = session.run(self.G, {
self.z: np.reshape(
zs[self.batch_size * i:self.batch_size * (i + 1)],
(self.batch_size, 1)
)
})
pg, _ = np.histogram(g, bins=bins, density=True)
return pd, pg
def _plot_distributions(self, session):
pd, pg = self._samples(session)
p_x = np.linspace(-self.gen.range, self.gen.range, len(pd))
f, ax = plt.subplots(1)
ax.set_ylim(0, 1)
plt.plot(p_x, pd, label='Real Data')
plt.plot(p_x, pg, label='Generated Data')
plt.title('GAN Visualization')
plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.legend()
plt.show()
def main(args):
model = GAN(
DataDistribution(),
GeneratorDistribution(range=8),
args.num_steps,
args.batch_size,
args.log_every,
)
model.train()
def parse_args():
parser = argparse.ArgumentParser()
parser.add_argument('--num-steps', type=int, default=1200,
help='the number of training steps to take')
parser.add_argument('--batch-size', type=int, default=12,
help='the batch size')
parser.add_argument('--log-every', type=int, default=10,
help='print loss after this many steps')
parses = parser.parse_args(args=[])#添加args=[]
return parses
if __name__ == '__main__':
main(parse_args())
![V=\frac{1}{m} \sum ^m_{i=1}[logD(x^{(i)})+log(1-D(G(z^{(i)})))]](http://img.e-com-net.com/image/info8/0d3b0e47753f4f28adfeec0928e7fb2d.gif)
![\triangledown _ {\theta,d} \ \frac{1}{m} \sum ^m_{i=1}[logD(x^{(i)})+log(1-D(G(z^{(i)})))]](http://img.e-com-net.com/image/info8/507bd69694124d528b75227d64e97724.gif)
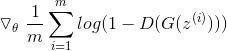
GAN的工程实践及基础代码_第1张图片](http://img.e-com-net.com/image/info8/26cdc73f5f9b4d5ab04a27dedcf463d0.jpg)
GAN的工程实践及基础代码_第2张图片](http://img.e-com-net.com/image/info8/6f912a42c203485a909cb066a8bb0c33.jpg)
GAN的工程实践及基础代码_第3张图片](http://img.e-com-net.com/image/info8/c5be52ddd652431a94328487b59b7357.jpg)
GAN的工程实践及基础代码_第4张图片](http://img.e-com-net.com/image/info8/0c22d2e53cb64cbc840052d47c557535.jpg)
GAN的工程实践及基础代码_第5张图片](http://img.e-com-net.com/image/info8/d6788dfc2a0e4eb1a110b312f082e43a.jpg)
GAN的工程实践及基础代码_第6张图片](http://img.e-com-net.com/image/info8/a2fbeb849ef742f6a8e48f78567b645c.jpg)
GAN的工程实践及基础代码_第7张图片](http://img.e-com-net.com/image/info8/599b7774e569455995c81f8eadaeff49.jpg)
GAN的工程实践及基础代码_第8张图片](http://img.e-com-net.com/image/info8/67f652589ffb45279df1a4beb3aad101.jpg)
GAN的工程实践及基础代码_第9张图片](http://img.e-com-net.com/image/info8/90ca5be134854776acce2f1773998b30.jpg)
GAN的工程实践及基础代码_第10张图片](http://img.e-com-net.com/image/info8/5b004790e412412f8e6f8313de2da07b.jpg)
GAN的工程实践及基础代码_第11张图片](http://img.e-com-net.com/image/info8/48676c7f8c5945b58b94626c5343a8cb.jpg)
GAN的工程实践及基础代码_第12张图片](http://img.e-com-net.com/image/info8/5ed11fece7f648c1abebc34164ee0ba0.jpg)
GAN的工程实践及基础代码_第13张图片](http://img.e-com-net.com/image/info8/b4cc155d699e4094ac3e82cbfc081b86.jpg)