(12)[arXiv16] Layer Normalization
计划完成深度学习入门的126篇论文第十二篇,多伦多大学的Hinton针对RNN等模型研究了对于Batch Norm的变种Layer Normalization。
本篇论文一作Jimmy Lei Ba同时也是Adam的作者。
ABSTRACT&INTRODUCTION
摘要
训练最先进的深层神经网络在计算上是昂贵的。减少训练时间的一种方法是使神经元的活动正常化。最近引入的一种称为批处理规范化的技术,使用在一小批训练用例上向神经元输入的和的分布来计算平均值和方差,然后使用这些平均值和方差来规范化每个训练用例上向该神经元输入的和。这大大减少了前馈神经网络的训练时间。然而,批处理归一化的效果取决于Minibatch的大小,如何将其应用到递归神经网络中尚不明显。
在本文中,我们将批处理归一化转化为层归一化,通过计算单个训练案例中所有层中神经元的累加输入归一化的均值和方差。和批处理归一化一样,我们也给每个神经元分配了自适应偏差和增益,这些偏差和增益在归一化后施加,但在非线性之前施加。与批处理规范化不同,层规范化在训练和测试时执行完全相同的计算。通过在每个时间步分别计算归一化统计量,也可以直接应用于递归神经网络。层归一化对于稳定递归网络中的隐态动力学非常有效。从经验上看,与以前发表的技术相比,层归一化可以大大减少训练时间。
介绍
在计算机视觉的各种监督学习任务[Krizhevsky et al., 2012]和语音处理[Hinton et al., 2012]中,使用某种版本的随机梯度下降训练的深度神经网络已经被证明大大优于之前的方法。但是最先进的深层神经网络通常需要很多天的训练。可以通过计算不同机器上训练用例的不同子集的梯度来加速学习,或者将神经网络本身分割到许多机器上[Dean et al., 2012],但这可能需要大量的通信和复杂的软件。随着并行化程度的增加,它还会导致收益迅速递减。正交法是对神经网络前向传递的计算进行修正,使学习变得更容易。最近,批处理规范化[Ioffe and Szegedy, 2015]被提议通过在深度神经网络中加入额外的规范化阶段来减少训练时间。标准化使用训练数据的平均值和标准差对每个相加输入进行标准化。使用批处理归一化训练的前馈神经网络即使使用简单的SGD也能更快地收敛。除了训练时间的改善,批统计量的随机性在训练过程中起到了调节作用。
尽管批处理标准化很简单,但它需要输入统计数据的运行平均值。在具有固定深度的前馈网络中,可以直接对每个隐藏层分别存储统计信息。然而,在递归神经网络(RNN)中,递归神经元输入的累加和往往随着序列的长度而变化,因此对递归神经网络进行批处理归一化似乎需要对不同的时间步长进行不同的统计。此外,批处理归一化不能应用于Online learning任务或者其他大型分布式模型,并且Minibatch只能是很小的时候。
本文介绍了一种简单的层归一化方法,用于提高各种神经网络模型的训练速度。与批处理归一化不同的是,该方法直接估计了隐藏层中神经元输入和的归一化统计量,因此该归一化不会在训练用例之间引入任何新的依赖关系。结果表明,层归一化方法对神经网络具有良好的归一化效果,提高了现有几种神经网络模型的训练时间和泛化性能。
Background
前馈神经网络是从输入模式x到输出向量y的非线性映射,考虑深度前馈神经网络的第l个隐含层,设al为该层神经元输入之和的向量表示。累加输入通过加权矩阵W l和自底向上输入hl的线性投影计算得到:
式中f(·)为单项非线性函数,wil为第i个隐藏单元的输入权值,bl i为标量偏置参数。利用基于梯度的优化算法对神经网络中的参数进行学习,并通过反向传播计算梯度。
深度学习的挑战之一是,一层的权重梯度高度依赖于前一层神经元的输出,特别是如果这些输出以高度相关的方式变化的话。批量标准化[Ioffe and Szegedy, 2015]的提出是为了减少这种不受欢迎的协变位移。该方法对训练用例中每个隐藏单元的相加输入进行规范化。具体来说,对于第l层的第i个累加输入,批处理归一化方法根据其方差在数据分布情况下对累加输入进行重新划分
其中,![]() 是对第l层第i个隐藏单元的输入进行归一化求和,gi为非线性激活函数之前的归一化激活的增益参数。注意,期望是在整个训练数据分布下。准确地计算Eq.(2)中的期望通常是不切实际的,因为它需要使用当前的权重集向前遍历整个训练数据集。相反,σ估计使用当前mini-batch实际样本。这就限制了小批处理的大小,很难应用于递归神经网络RNN。
是对第l层第i个隐藏单元的输入进行归一化求和,gi为非线性激活函数之前的归一化激活的增益参数。注意,期望是在整个训练数据分布下。准确地计算Eq.(2)中的期望通常是不切实际的,因为它需要使用当前的权重集向前遍历整个训练数据集。相反,σ估计使用当前mini-batch实际样本。这就限制了小批处理的大小,很难应用于递归神经网络RNN。
Layer normalization
现在我们考虑层归一化方法,它是为了克服批处理归一化的缺点而设计的。
请注意,一层输出的变化往往会导致下一层的汇总输入发生高度相关的变化,特别是对于输出可能发生很大变化的ReLU单元。这表明,“协变位移”问题可以通过固定每个层中相加输入的平均值和方差来减少。因此,我们计算同一层中所有隐藏单元的层归一化统计量如下:
其中H表示层中隐藏的单元数。Eq.(2)和Eq.(3)的不同之处在于,在层归一化下,层中所有隐藏的单元都有相同的归一化项µ和σ,但不同的训练情况下有不同的归一化条件。与批处理规范化不同,layer normaliztion对小批处理的大小没有任何限制,可以在批处理大小为1的Online learning任务下使用。
Layer normalized recurrent neural networks
最近的序列到序列模型[Sutskever et al., 2014]利用紧凑的递归神经网络来解决自然语言处理中的序列预测问题。在NLP任务中,针对不同的训练案例有不同的句子长度是很常见的。这在RNN中很容易处理,因为每个时间步都使用相同的权重。但是,当我们以明显的方式对RNN应用批处理规范化时,我们需要计算和存储序列中每个时间步骤的独立统计信息。如果测试序列比任何训练序列都长,这就有问题了。层归一化不存在这样的问题,因为它的归一化项只依赖于当前时间步长对层输入的累加。它也只有一组增益和偏差参数在所有时间步骤中共享。在标准RNN中,递归层的累加输入由当前输入xt和之前的隐藏状态ht1向量计算得到,ht1向量的计算结果为![]() 。层归一化递归层重新居中,并使用类似于公式(3)的额外归一化项重新伸缩其激活。
。层归一化递归层重新居中,并使用类似于公式(3)的额外归一化项重新伸缩其激活。
其中,Whh为隐含权重的递归隐藏,Wxh为隐含权重的自下而上输入,![]() 是两个向量之间的element-wise。b和g定义为与ht相同尺寸的偏置和增益参数。
是两个向量之间的element-wise。b和g定义为与ht相同尺寸的偏置和增益参数。
在标准的RNN中,在每一个时间步长时,递归单元的平均输入和的大小有增长或收缩的趋势,导致梯度的爆炸或消失。在一层归一化的RNN中,归一化项使得将所有累加的输入重新缩放到一层是不变的,这使得隐藏到隐藏的动态更加稳定。
Related work
批量归一化以前已经扩展到递归神经网络[Laurent et al., 2015, Amodei et al., 2015, Cooijmans et al., 2016]。前期工作[Cooijmans et al., 2016]表明,通过对每个时间步保持独立的归一化统计量,可以获得最优的递归批处理归一化性能。作者证明,初始化循环批处理归一化层中的增益参数到0.1对模型的最终性能有显著的影响。我们的工作也与体重正常化有关[Salimans and Kingma, 2016]。在权值归一化中,输入权值的L2范数被用来归一化加起来的输入到神经元的值,而不是方差。使用期望统计量进行权值归一化或批处理归一化,相当于对原始前馈神经网络进行了不同的参数化。在参数中研究了ReLU网络的再参数化[Neyshabur et al., 2015]。然而,我们提出的层归一化方法并不是对原始神经网络的重新参数化。因此,与其他方法相比,层归一化模型具有不同的不变性,我们将在下一节中研究这些方法。
Analysis
1. Invariance under weights and data transformations
提出的层归一化与批处理归一化和权值归一化有关。虽然,他们的正常化标量计算不同,这些方法可以概括为规范总结输入人工智能神经元通过两个标量µ和σ。他们还学习了自适应偏差b,并在归一化后为每个神经元获得g。
注意,对于层标准化和批处理规范化,根据公式,2和3µ和σ计算。在权重正常化![]() 。
。
Weight re-scaling and re-centering
权重重缩放和重定心:首先,观察在批处理归一化和权重归一化下,单个神经元的权值wi的重缩放对神经元的归一化和输入没有影响。更精确地说,下批处理和权重正常化,如果权重向量乘以δ,两个标量和σδ也将扩大。规格化求和输入在缩放前后保持不变。因此,批处理和权重标准化对于权重的重新缩放是不变的。另一方面,层归一化对于单个权向量的缩放并不是不变的。相反,层归一化对于整个权矩阵的缩放是不变的,对于权矩阵中所有输入权的移位也是不变的。要有两套模型参数θ,θ0的权重矩阵W和W 0不同比例因子δ和所有传入的重量Wγ0也转移了一个常数向量,是![]() 。在层归一化下,两种模型可以有效地计算相同的输出:
。在层归一化下,两种模型可以有效地计算相同的输出:
请注意,如果规范化只应用于权重之前的输入,那么模型对于权重的重新缩放和重新定心就不是不变的。
Data re-scaling and re-centering
数据重定标和重定中心:通过验证神经元的相加输入在变化下保持不变,我们可以看出所有的归一化方法对于数据集的重定标都是不变的。此外,层正常化不变re-scaling个人培训的情况下,因为正常化标量和σEq。(3)只取决于当前输入数据。让x0 重新调整大小获得的新数据点通过δx。然后我们有
很容易看出,在层归一化的情况下,单个数据点的重新缩放并不会改变模型的预测。与层归一化中权重矩阵的再中心化相似,我们也可以看出批处理归一化对数据集的再中心化是不变的。
2. Geometry of parameter space during learning
研究了模型在参数重定心和重定标下预测的不变性。然而,在不同的参数化下,学习的行为可能会非常不同,即使模型表达的是相同的底层函数。在这一节中,我们将通过几何和参数空间的流形来分析学习行为。我们表明,归一化标量σ可以隐式地减少学习速率,使学习更加稳定。
Riemannian metric
统计模型中的可学习参数构成光滑流形,由模型的所有可能的输入输出关系组成。对于输出为概率分布的模型,度量流形上两点分离的自然方法是模型输出分布之间的Kullback-Leibler散度。在KL散度度规下,参数空间为黎曼流形。黎曼流形的曲率完全由其黎曼度量来表示,黎曼度量的二次形式记为ds2。这是在参数空间中切线空间中一点的无限小的距离。直观地说,它度量了参数空间沿切线方向输出的模型的变化。以前研究过KL下的黎曼度量[Amari, 1998],结果表明,在二阶泰勒展开下,利用Fisher信息矩阵可以很好地近似黎曼度量:
δ是一个小的改变参数。上面的黎曼度量给出了参数空间的几何视图。下面对黎曼度量的分析为规范化方法如何帮助训练神经网络提供了一些见解。
The geometry of normalized generalized linear models
我们把几何分析的重点放在广义线性模型上。下面的分析结果可以很容易地应用于理解具有块对角逼近Fisher信息矩阵的深层神经网络,其中每个块对应于单个神经元的参数。
广义线性模型(GLM)可以用权向量w和偏置标量b作为指数族输出分布的参数。为了与前几节一致,我们可以将广义线性模型的对数似然式写成:
f(·)的传递函数的非线性神经网络的模拟,f 0(·)传递函数的导数,η(·)是一个实值函数和c(·)日志的配分函数。φ是一个常数,天平输出方差。假设h维输出向量![]() 采用独立于H的GLMs和
采用独立于H的GLMs和![]()
![]() 。设W为权重矩阵,其中行为单个GLMs的权重向量,b为长度H的偏置向量,vec(·)为Kronecker向量算子。费舍尔信息矩阵的多维GLM的参数
。设W为权重矩阵,其中行为单个GLMs的权重向量,b为长度H的偏置向量,vec(·)为Kronecker向量算子。费舍尔信息矩阵的多维GLM的参数![]() 是数据特征与输出协方差矩阵的期望Kronecker乘积:
是数据特征与输出协方差矩阵的期望Kronecker乘积:
得到归一化后运用规范化方法来总结输入原始模型通过和σ。不失一般性,我们表示F费舍尔信息矩阵的归一化多维GLM与其他增益参数![]() :
:
Implicit learning rate reduction through the growth of the weight vector
内隐学习速率减少通过权向量的增长:注意,比较标准的漠视,块沿权向量F ij wi方向扩展的增益参数和标量σi正常化。如果权向量wi的范数增长两倍大,即使模型s的输出保持不变,Fisher信息矩阵也会不同。沿着wi曲率方向会改变1/2倍,因为σi也将两倍。因此,对于归一化模型中相同参数的更新,权向量的范数有效地控制了权向量的学习率。在学习过程中,改变大范数权重向量的方向比较困难。因此,标准化方法是否对权重向量有隐式的“Early Stop”效应,并有助于稳定向收敛方向学习。
Learning the magnitude of incoming weights
学习传入权值的大小:在规范化模型中,传入权值的大小由增益参数显式参数化。我们比较了在学习过程中,模型输出在正则化GLM中更新增益参数和在初始参数化下更新等效权值之间的变化。沿F中的增益参数的方向捕获传入权重的大小的几何图形。我们证明了黎曼度量沿着标准GLM的输入权值的大小是由其输入的范数来衡量的,而批量归一化模型和层归一化模型的增益参数的学习只取决于预测误差的大小。因此,在归一化模型中学习输入权值的大小比在标准模型中对输入及其参数的缩放更具有鲁棒性。详细推导见附录。
Experimental results
我们对6个任务进行了层归一化实验,重点研究了递归神经网络:图像-句子排序、问答、语境语言建模、生成模型、手写序列生成和MNIST分类。除另有说明外,层归一化的默认初始化是将实验中的自适应增益设置为1,偏差设置为0。
1 Order embeddings of images and language
在本实验中,我们对Vendrov等[2016]最近提出的order- embedded模型进行分层归一化,学习图像和句子的联合嵌入空间。我们遵循与Vendrov等人[2016]相同的实验协议,并修改其公开可用的代码,纳入使用Theano [Team et al., 2016]的layer norm1。将Microsoft COCO数据集[Lin et al., 2014]中的图像和句子嵌入到一个公共向量空间中,使用GRU [Cho et al., 2014]对句子进行编码,使用预先训练好的VGG ConvNet [Simonyan and Zisserman, 2015] (10-crop)的输出对图像进行编码。orderembed模型将图像和句子表示为2级偏序,并将Kiros等[2014]中使用的余弦相似度评分函数替换为非对称的余弦相似度评分函数。
我们训练了两种模型:基线订单嵌入模型和应用于GRU的层归一化模型。在每300次迭代之后,我们在一个保留的验证集上计算Recall@K (R@K)值,并在R@K改进时保存模型。然后在5个单独的测试集上评估性能最好的模型,每个测试集包含1000幅图像和5000个标题,并报告平均结果。两种模型都使用Adam [Kingma和Ba, 2014],具有相同的初始超参数,并且两种模型都使用Vendrov等人[2016]使用的相同架构选择进行训练。我们请读者参阅附录,了解如何将层规范化应用于GRU。
图1展示了模型的验证曲线,包括和不包括层归一化。我们为图像检索任务绘制R@1、R@5和R@10。我们观察到,层规范化在所有指标上提供了每次迭代的加速,并且在基线模型所需时间的60%内收敛到最佳验证模型。
在表2中,我们报告了测试集的结果,从中我们可以观察到,层归一化也改善了原始模型的泛化。我们报告的结果在RNN嵌入模型方面是最先进的,只有Wang等[2016]的结构保持模型在这个任务上报告了更好的结果。然而,它们在不同的条件下(1个测试集而不是平均值除以5)进行评估,因此不能直接比较。
2 Teaching machines to read and comprehend
为了将层归一化与最近提出的递归批处理归一化进行比较[Cooijmans et al., 2016],我们在Hermann et al.[2015]引入的CNN语料库上训练了一个单向的专注读者模型。这是一个问答任务,其中关于文章的查询描述必须通过填写空格来回答。这些数据是匿名的,这样实体就可以得到随机的令牌来防止退化的解决方案,在训练和评估过程中,退化的解决方案是一致的。我们遵循与Cooijmans等人[2016]相同的实验协议,并修改他们的公共代码,纳入使用Theano [Team et al., 2016]的layer norm2。我们得到了Cooijmans et al.[2016]使用的预处理数据集,与Hermann et al.[2015]的原始实验不同的是,每个段落限制在4个句子。Cooijmans等[2016]采用了两种递归批量归一化的变体:一种是BN只应用于LSTM,而另一种是BN在整个模型中无处不在。在我们的实验中,我们只在LSTM中应用层归一化。
实验结果如图2所示。我们观察到,层归一化不仅训练得更快,而且在基线和BN变量上收敛到更好的验证结果。Cooijmans等[2016]认为BN的尺度参数必须谨慎选择,在他们的实验中设置为0.1。我们对1.0和0.1尺度的初始化都进行了层归一化实验,发现前者的模型性能明显更好。这说明层归一化对初始尺度不像递归BN那样敏感。
3 Skip-thought vectors
https://github.com/ryankiros/skip-thoughts
https://github.com/NVIDIA/cnmem
实验结果如图3所示。我们观察到应用层归一化在基线上的加速和1M迭代后更好的最终结果如表3所示。我们还让具有层规范化的模型进行为期一个月的培训,从而在除一个任务之外的所有任务中进一步提高性能。我们注意到性能原始报告的结果和我们报告的结果之间的差异可能是由于这样一个事实,即公开可用的代码在解码器的每个时间步上都没有条件,而在原始模型中有条件。
4 Modeling binarized MNIST using DRAW
图4显示了前100个epoch的测试变分界限。它突出了应用层归一化的加速好处,层归一化的绘制收敛速度几乎是基线模型的两倍。
经过200个epoch后,基线模型收敛到测试数据上的变分log likelihood为82.36 nats,层归一化模型得到82.09 nats。
5 Handwriting sequence generation
以往的实验主要是对长度在10 - 40之间的NLP任务进行RNNs的检测。为了证明层归一化在长序列上的有效性,我们使用IAM在线笔迹数据库进行笔迹生成任务[Liwicki and Bunke, 2005]。IAM-OnDB由221位不同作者的手写诗句组成。当给定输入字符串时,目标是预测白板上相应手写线的x和y笔坐标序列。总共有12179个手写行序列。输入的字符串通常超过25个字符,平均字迹长度约为700。我们使用了Graves[2013]中(5.2)节相同的模型架构。模型结构由3个隐藏层组成,其中400个LSTM单元在输出层产生20个二元高斯混合分量,以及一个尺寸为3的输入层。字符序列用单热向量编码,因此窗口向量的大小为57。窗口参数使用10个高斯函数的混合,需要30个参数向量。总重量增加到约370万磅。模型使用小批量的大小为8和Adam [Kingma and Ba, 2014]优化器进行培训。
小批量和长序列的组合使得拥有非常稳定的隐藏动态非常重要。图5显示了层归一化收敛到类似于基线模型的日志似然,但是速度快得多。
6 Permutation invariant MNIST
除了RNNs,我们还研究了前馈网络中的层归一化问题。我们展示了层归一化与批处理归一化在排列不变的MNIST分类问题上的比较。从前面的分析可以看出,层归一化对于输入的重新缩放是不变的,这是内部隐藏层所需要的。但这对于logit输出来说是不必要的,因为logit输出的预测置信度是由逻辑的规模决定的。我们只对完全连接的隐藏层应用层归一化,它排除了最后一个softmax层。所有模型都使用55000个训练数据点和Adam [Kingma and Ba, 2014]优化器进行了训练。对于较小的批处理规模,使用无偏估计量计算批处理标准化的方差项。图6的实验结果突出了层归一化对批处理大小的鲁棒性,与应用于所有层的批处理归一化相比,具有更快的训练收敛性。
7 Convolutional Networks
我们还对卷积神经网络进行了实验。在我们的初步实验中,我们观察到层归一化在没有归一化的基础模型上提供了一个加速,但是批处理归一化优于其他方法。对于完全连接的层,一个层中的所有隐藏单元都倾向于对最终的预测做出类似的贡献,对一个层的汇总输入进行重新定心和缩放效果良好。然而,对于卷积神经网络,类似贡献的假设不再成立。接收域位于图像边界附近的大量隐藏单元很少被打开,因此与同一层中的其他隐藏单元具有非常不同的统计信息。我们认为,要使对流网络的层归一化工作良好,还需要进一步的研究。
Conclusion
为了加快神经网络的训练速度,本文引入了层归一化方法。对层归一化与批处理归一化、权值归一化的不变性进行了理论分析。我们证明了层归一化对于每个训练用例的特征移动和缩放是不变的。实验结果表明,该方法对小批量、长序列的递归神经网络最有效。
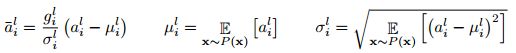
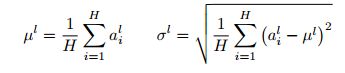
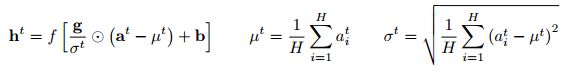
![(12)[arXiv16] Layer Normalization_第1张图片](http://img.e-com-net.com/image/info8/79e3316b69df4d11ac2b62b713a18d55.jpg)
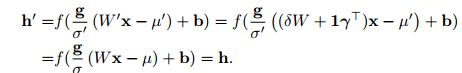
![(12)[arXiv16] Layer Normalization_第2张图片](http://img.e-com-net.com/image/info8/89252e10a9f64eeda4f2b2181a1fdef3.jpg)
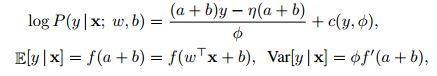

![(12)[arXiv16] Layer Normalization_第3张图片](http://img.e-com-net.com/image/info8/5af7a753a95d4926b7c8196e000a6b9d.jpg)
![(12)[arXiv16] Layer Normalization_第4张图片](http://img.e-com-net.com/image/info8/7c7885d606e84ab4bf9da0d2434cb1b2.jpg)
![(12)[arXiv16] Layer Normalization_第5张图片](http://img.e-com-net.com/image/info8/d6cb984784884ed798cd997eb6646dc8.jpg)
![(12)[arXiv16] Layer Normalization_第6张图片](http://img.e-com-net.com/image/info8/91926e1957ba4c478d412794634096b6.jpg)
![(12)[arXiv16] Layer Normalization_第7张图片](http://img.e-com-net.com/image/info8/c0e820ae2239486aa4ee6d876ee92ab9.jpg)
![(12)[arXiv16] Layer Normalization_第8张图片](http://img.e-com-net.com/image/info8/a3b39bea8a1143009cba3ff30b2491b4.jpg)
![(12)[arXiv16] Layer Normalization_第9张图片](http://img.e-com-net.com/image/info8/e44227ce21eb4067bb57761dadb0c28d.jpg)
![(12)[arXiv16] Layer Normalization_第10张图片](http://img.e-com-net.com/image/info8/bc37e4e8bec842d3a16699f7b0b23734.jpg)
![(12)[arXiv16] Layer Normalization_第11张图片](http://img.e-com-net.com/image/info8/25eea79ab3194ce1a60387fcb03f342b.jpg)