Python之高等数学（定积分与不定积分，重积分）

• 先说一下定积分与不定积分我的简单理解。。。。。。。。
• 不定积分只是导数的逆运算，所以也叫做反导数。
• 
• 
• 而定积分是求一个函数的图形在一个闭区间上和 x 坐标轴围成的面积

Python实现求解的时候，我们不需要复制数学推导，就直接求面积出来就行

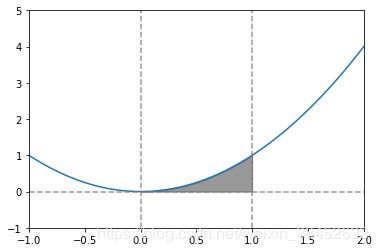
# 计算定积分

def f(x):
    return x**2

n = np.linspace(-1,2,num = 50)
n1 = np.linspace(0,1,num = 50)
plt.plot(n,f(n))
plt.fill_between(n1,0,f(n1),color = 'k',alpha = 0.4)
plt.xlim(-1,2)
plt.ylim(-1,5)

plt.axvline(0,color = 'gray',linestyle = '--',alpha=0.8)  
plt.axvline(1,color = 'gray',linestyle = '--',alpha=0.8)  
plt.axhline(0,color = 'gray',linestyle = '--',alpha=0.8)  
# 辅助线

area = 0
xi = 0
for i in range(len(n1))[:-1]:
    xi = (n1[i]+n1[i+1])/2
    area += (n1[i+1]-n1[i])*f(xi)
print(area)
# 计算0-1上的定积分值

0.3332986255726781

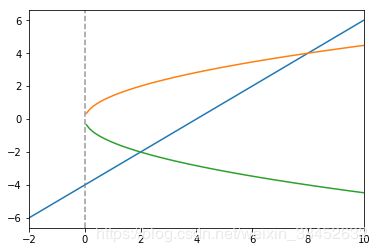
# 计算图形面积

def f11(x):
    return (2*x)**0.5
def f12(x):
    return -(2*x)**0.5
def f2(x):
    return x - 4

n = np.linspace(10,-2,num = 100)
plt.plot(n,f2(n))

n1 = n[n>=0]
plt.plot(n1,f11(n1))
plt.plot(n1,f12(n1))
plt.xlim(-2,10)
plt.axvline(0,color = 'gray',linestyle = '--',alpha=0.8)  
# 辅助线

y = np.linspace(-2,4,num = 100)
area = 0
for i in range(len(y))[:-1]:
    y_ = y[i+1]-y[i]
    area += y_ * (y[i+1] + 4 - y[i+1]**2/2)
print(area)
# 计算[-2,4]上的定积分值

17.998163452708912

多元函数的概念
定义：设 D是 R2 的一个非空子集，称映射 f : D → R为定义在 D上的二元函数，通常记为
z = f (x, y), (x, y) ∈ D 或 z = f (P), P ∈ D
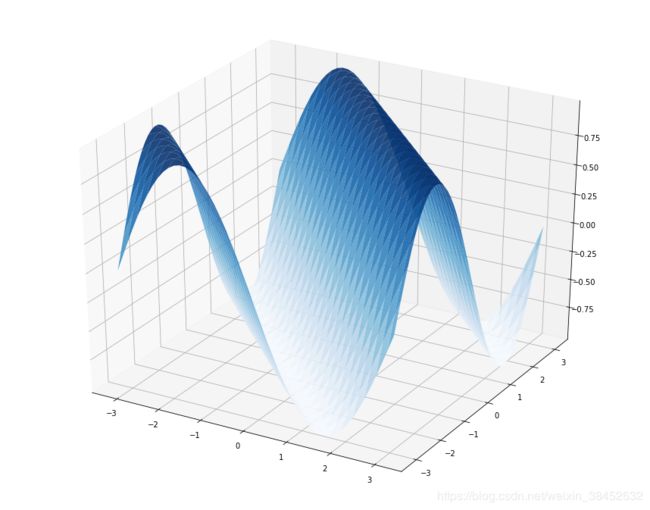
其中点集 D称为该函数的定义域， x和 y称为自变量， z称为因变量☺ 二元函数 z = Sin(x + y)

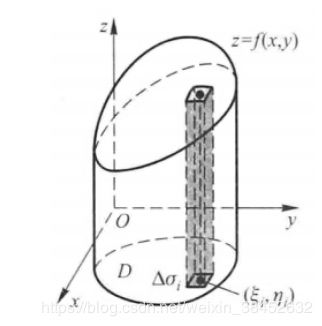
二重积分的概念与性质
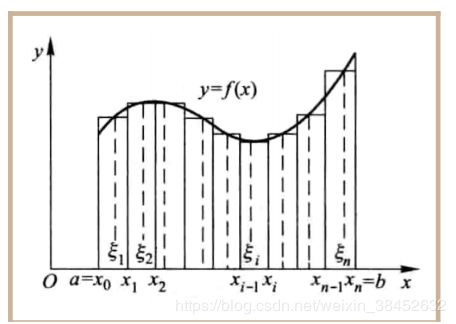
定义：设函数 f(x, y) 是有界闭区域 D 上 的 有 界 函 数 ， 将 闭 区 域 D 任 意 分 成 n 个 小 闭 区 域 ，
Δδ1, Δδ2, ..., Δδn, 其中 Δδi 表示第 i个小闭区域， 也表示它的面积 .在每个小闭区域内任取一点 (ξi, ηi) 做乘积
f (ξi, ηi) Δδi(i = 1, 2, ..., n)，并做求和

# z = sin(x+y)

from mpl_toolkits.mplot3d import axes3d
# 导入3d绘图包

X = np.linspace(-np.pi,np.pi,num = 50)
Y = np.linspace(-np.pi,np.pi,num = 50)
X, Y = np.meshgrid(X, Y)
Z = np.sin(X+Y)
#print(Z)

fig = plt.figure(figsize = (15,12))
ax = fig.gca(projection='3d')  
ax.view_init(elev=None, azim=None)
# 创建3d绘图空间
# view_init → 设置视角，elev设置z平面的角度，azim设置xy平面角度

ax.plot_surface(X, Y, Z, rstride=2, cstride=2,cmap='Blues',alpha = 0.9)
# rstride, cstride : 不同方向的采样距离