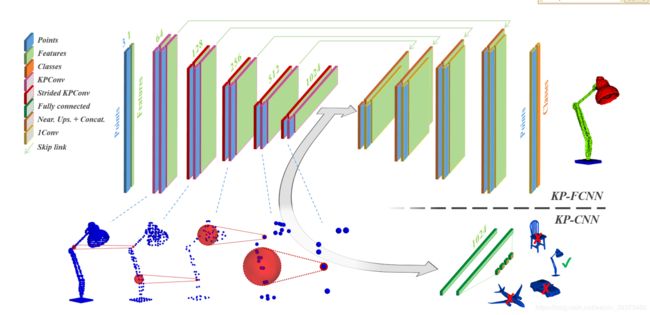
【3D计算机视觉】KPConv——点云上的可形变卷积网络
《KPConv: Flexible and Deformable Convolution for Point Clouds》阅读笔记
- 一、主要贡献
- 二、模型
- 2.1 定义在点云上的核函数
- 2.2 Rigid or Deformable Kernel
- Rigid Kernel
- Deformable Kernel
- 2.3 Kernel Point Network Layers
- Subsampling to deal with varying densities
- Pooling layer
- KPConv layer
- 网络的超参数
- 2.4 Kernel Point Network Architectures
- 三、实验结果
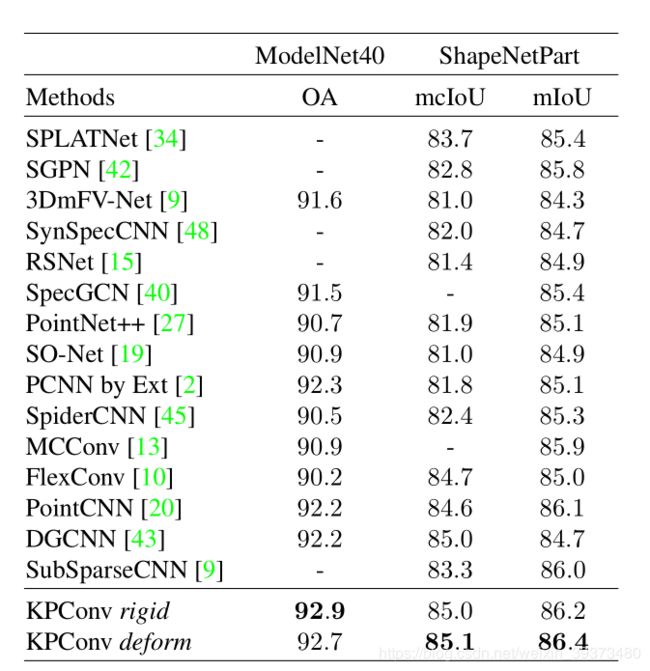
- 3.1 简单任务（分类+部件分割）
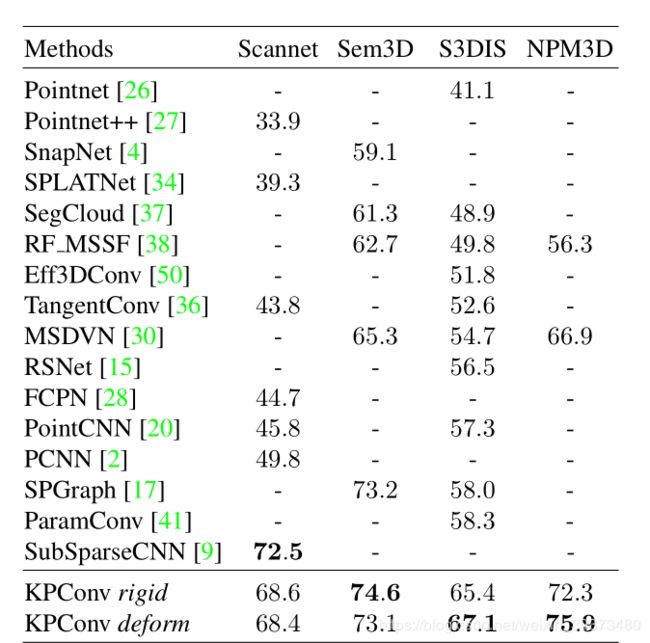
- 3.2 复杂任务（真实场景分割）
Github代码：https://github.com/HuguesTHOMAS/KPConv
论文：https://arxiv.org/abs/1904.08889
一、主要贡献
这是PointNet的作者Charles R. Qi的一篇文章，在许多分割的任务上都达到了极好的效果，超过了当前的State of the art七八个点。这一篇的贡献点总结如下：
- 提出了一种基于Kernel Point的新型点云卷积。相当于将Kernel Point当成了每个点的参照物，去计算与这些Kernel Point的权重去更新每个点；
- 提出了两种不同类型的Kernel Point，一种是刚性的Rigid Kernel，相当于均匀分布在每个点的周围球面；一种是可变的Deformable Kernel ，通过在刚性的基础上通过网络去学习它的位置变化；
- 整个网络GPU占用少、速度快，可以在不定个数的点云上直接训练，因此效果也好。
二、模型
2.1 定义在点云上的核函数
首先定义一下点云上的某个点 x i ∈ P ∈ R N × 3 x_i\in P \in R^{N\times 3} xi∈P∈RN×3以及其对应的特征 f i ∈ F ∈ R N × D f_i\in F \in R^{N\times D} fi∈F∈RN×D，通常由kenel g g g所定义的点云的卷积可以写成如下的形式：
( F ∗ g ) ( x ) = ∑ x i ∈ N x g ( x i − x ) f i (F*g)(x) = \sum_{x_i \in N_x} g(x_i-x )f_i (F∗g)(x)=xi∈Nx∑g(xi−x)fi其中 N x N_x Nx代表其某个局部邻域，可以看做是某个中心点以半径 r r r画出的一个球形邻域，即 N x = { x i ∈ P ∣ ∣ ∣ x i − x ∣ ∣ ≤ r } N_x = \{x_i \in P | ||x_i-x||\leq r\} Nx={xi∈P∣∣∣xi−x∣∣≤r}
在不同的工作中，往往上面公式中的核函数 g g g才是关键， g g g取以 x x x为中心的相邻点作为输入。在这篇文章中，作者同其他工作一样将局部的区域中心化，即对于每一个点 x i x_i xi，可以通过中心化 y i = x i − x y_i = x_i-x yi=xi−x 将其转换成 y i y_i yi，因此， B r 3 = { y ∈ R 3 ∣ ∣ ∣ y ∣ ∣ ≤ r } B^3_r= \{y\in R^3 | ||y||\leq r\} Br3={y∈R3∣∣∣y∣∣≤r}， 这样网络就拥有了平移不变性。与其他工作不同的是，作者定义了一组Kernel Points， { x k ^ ∣ k < K } ∈ B r 3 \{\hat{x_k}|k<K\}\in B^3_r {xk^∣k<K}∈Br3 以及它们对应的权重 { W k ∣ k < K } ∈ R D i n × D o u t \{{W_k}|k<K\}\in R^{D_{in} \times D_{out}} {Wk∣k<K}∈RDin×Dout，通过将每个点周围的Kernel Point作为其参照物，去进行特征的聚合。
最终，点云上的核函数可以定义为：
g ( y i ) = ∑ k < K h ( y i , x k ^ ) W k g(y_i)=\sum_{k<K}h(y_i,\hat{x_k})W_k g(yi)=k<K∑h(yi,xk^)Wk其中 h h h代表 x k ^ \hat{x_k} xk^和 y i y_i yi的相关性，当他们两个接近的时候其会比较高。
h ( y i , x k ^ ) = m a x ( 0 , 1 ∣ ∣ y i − x k ^ ∣ ∣ σ ) h(y_i,\hat{x_k}) = max(0,1\frac{||y_i-\hat{x_k}||}{\sigma}) h(yi,xk^)=max(0,1σ∣∣yi−xk^∣∣)其中 σ \sigma σ是Kernel Points的影响距离，将根据输入密度进行选择。因此，每个点的特征 f i f_i fi乘以所有的Kernel的权重矩阵，相关系数 h i k h_{ik} hik取决于它相对于Kernel Points的位置。
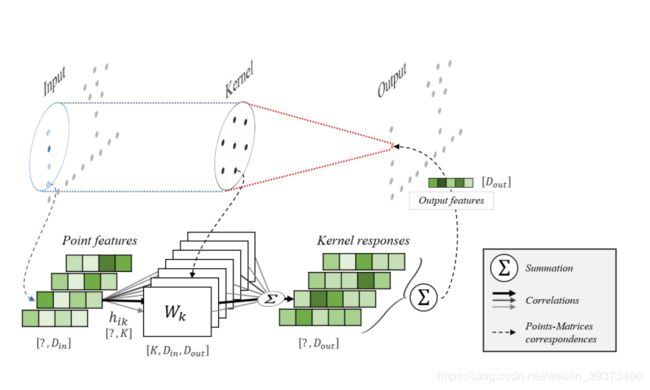
2.2 Rigid or Deformable Kernel
Kernel Points 的选取相当于这篇文章的核心问题，它们需要研究出一个通用的方案，对于任意的Kernel Points数量 K K K，都可以在空间上面构建这些Kernel Points。论文提出了两种解决方案：
Rigid Kernel
作者在文章中说，Rigid Kernel 对于一些简单的任务表现得较好。作者首先选择通过求解一个优化问题来放置Kernel Points，其中每个点对其他点施加一个斥力。这些点被限制在具有吸引力的球面上，其中一个点被限制在中心。最终,周围的点被限制在平均半径1.5σ,确保每个Kernel Points之间的影响力有小幅度的重叠。
具体的数学推导其实是求解一个优化问题，即希望K个Kernel Points在球面上离得足够远，又离球心不要太远。目标方程的第一部分是希望Kernel Points之间彼此不要太近：
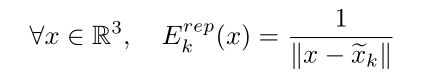
第二个部分是希望与中心点不要太远
所以最后的目标方程如下：
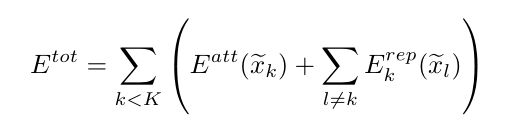
通过论文的实验结果可以看到选取不同的超参数K时所得到的Kernel Points的位置。
Deformable Kernel
作者首先考虑给予不同的层不同的初始化Kernel Points，但是他们认为这样并不能给予网络更多的表述能力，因此他们最后参考了Deformable Convolutional Networks的设计，对于每个Kernel Points学习一个位移 Δ ( x ) \Delta(x) Δ(x)。所以最终卷积的形式如下：
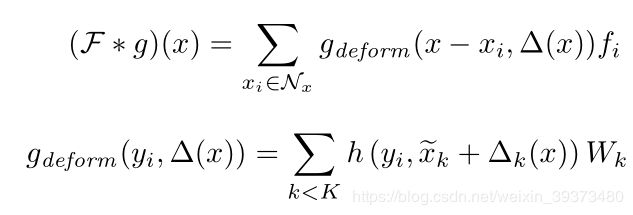其通过对一个Rigid Kernel的KPNet，将特征从 D i n D_{in} Din映射到 3 K 3K 3K维度，并在训练的时候给予0.1倍的学习率去进行训练。
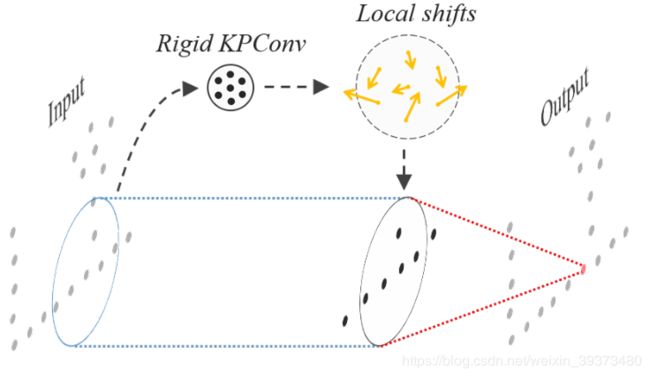
但是这里会出现一个问题，由于点云的稀疏性，会容易出现一个Kernel Points的影响范围内没有出现任何点。因此网络需要去学习一个位移去使得这些Kernel Points去拟合点云的空间形状。这里作者设计了两个Loss，fitting loss用来使得这些Kernel Points形状与点云相似，repulsive loss 使得她们彼此之间不会太近。
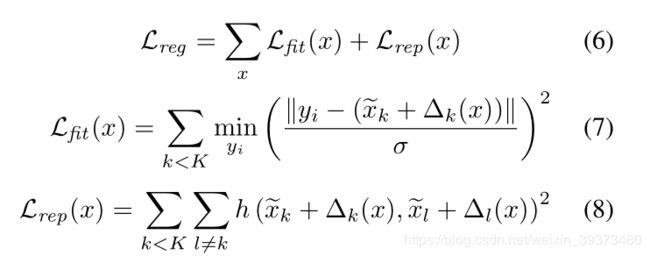
2.3 Kernel Point Network Layers
Subsampling to deal with varying densities
作者使用采样策略来控制每一层输入点的密度。为了保证采样点位置的空间一致性，他们采用网格采样（即通过空间划分网格，对每个网格内采取中心点）。因此每一个网格的重心，被作为采样点。
Pooling layer
为了使得网络感受野不断增大，网络需要在后面的层不断减少点的个数。文章中有两种下采样的方法：
- 逐点作为中心点的计算kernel point的权重，更新点的feature，最后再利用Max pooling减少点的个数；
- 采样一些点作为中心点，同上，但最后不做Max pooling。
KPConv layer
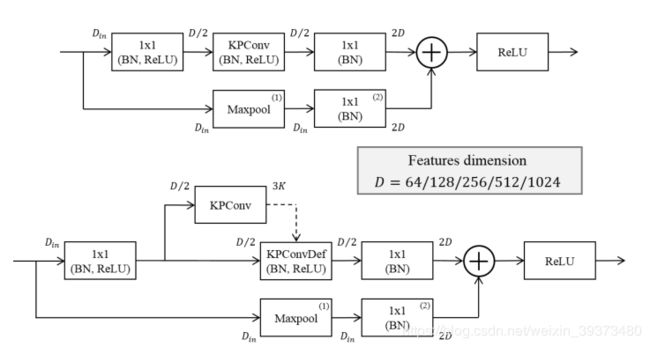
KPConv的输入是输入点云 P ∈ R N × 3 P\in R^{N\times 3} P∈RN×3以及它们对应的特征 F ∈ R N × D i n F\in R^{N\times D_{in}} F∈RN×Din。同时还需要计算一个邻居索引的矩阵 n ∈ [ 1 , N ] N ′ , n m a x n\in [1,N]^{N',n_{max}} n∈[1,N]N′,nmax，其索引的值为1~N，N’个点各有 n m a x n_{max} nmax个邻居。如果是Deformable Kernel的话网络还会学习一个 3 k 3k 3k的位移矩阵（如下图2）。
网络的超参数
对于网络的每一层 l a y e r j layer_j layerj，有网格的宽度cell size d l j dl_j dlj。 Kernel Points的影响范围 σ j = ∑ × d l j \sigma_j = \sum \times dl_j σj=∑×dlj。对于刚性的卷积核，卷积的半径为 2.5 σ j 2.5\sigma_j 2.5σj，其 Kernel Points的平均半径 1.5 σ j 1.5 \sigma_j 1.5σj。对于可形变的卷积核， r j = ρ × d l j r_j = ρ\times dl_j rj=ρ×dlj， ρ ρ ρ 和 ∑ \sum ∑ 为整个网络的比例系数。通过交叉验证作者得到了： K = 15 K = 15 K=15, Σ = 1.0 Σ = 1.0 Σ=1.0 和 ρ = 5.0 ρ = 5.0 ρ=5.0。第一次下采样的cell size d l 0 dl_0 dl0取决于数据的大小，之后 d l j + 1 = 2 × d l j dl_{j+1} = 2 \times dl_j dlj+1=2×dlj。
2.4 Kernel Point Network Architectures
三、实验结果
3.1 简单任务（分类+部件分割）
3.2 复杂任务（真实场景分割）
