将一维时间序列转化成二维图片

原文地址：Encoding Time Series as Images

虽然现在深度学习在计算机视觉和语音识别上发展得很好，但是碰到时间序列时，构建预测模型是很难的。原因包括循环神经网络较难训练、一些研究比较难以应用，而且没有现存与训练网络，1D-CNN 不方便。

但是如果使用 Gramian Angular Field (GAF)，可以把时间序列转成图片，充分利用目前机器视觉上的优势。

这篇文章会包括下面这些内容：

• 数学先验知识；
• Gram Matrix 为何可以为单变量的时间序列构建一个好的二维表示；
• Gram Matrix 点积为何不能表示 CNN 的数据；
• 为 CNN 准备好 Gram Matrix 结构的操作是什么；

还会包括 Python 代码：

• 用于 GAF 计算的 numpy 工具；

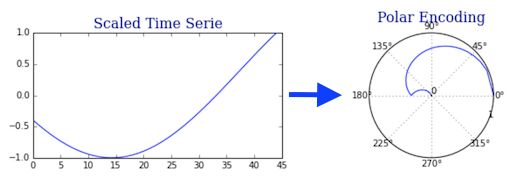
下面的动图展示了对数据进行极坐标编码，然后对生成的角度进行类似于 Gram 矩阵的操作：

1. 数学先验知识

GAF 的数学方法与内积与相应的 Gram 矩阵有很深的联系。

1.1. 点积（Dot product）

内积是两个向量之间的运算，用来度量它们的「相似性」。它允许使用来自传统 Euclidian Geometry 的概念：长度、角度、第二维度和第三维度的正交性。

在二维空间上，两个向量 $u$ 和 $v$ 之间的内积定义为：
$$⟨u,v⟩=u_1\cdot v_1+u_2\cdot v_2$$
或者：
$$⟨u,v⟩=\Vert u\Vert \cdot \Vert v\Vert \cdot \cos (\theta )$$
如果 $u$ 和 $v$ 的范数为 1，我们就得到：
$$⟨u,v⟩=cos(\theta )$$
因此，如果处理的是单位向量，他们的内积就只由角度 $\theta$ 决定了，这个角度可以用弧度来表示。计算出来的值会在 [-1,1] 内。记住这些定理，在本文的其他位置会用到。

注意：在 Euclidian 集合（n 维）中，两个向量的内积的正式定义为：
$$⟨u,v⟩=\sum _{i=1}^n{u}_i\cdot v_i$$

1.2. Gram 矩阵（Gram Matrix）

在线性代数和几何中，Gram 矩阵是一个有用的工具，它经常用于计算一组向量的线性相关关系。

定义：一组 n 个向量的 Gram 矩阵是由每一对向量的点积定义的矩阵。从数学上讲，这可以解释为：
$$G=\left(\begin{array}{cccc}⟨u_1,v_1⟩& ⟨u_1,v_2⟩& \cdots & ⟨u_1,v_n⟩\\ ⟨u_2,v_1⟩& ⟨u_2,v_2⟩& \cdots & ⟨u_2,v_n⟩\\ ⋮& ⋮& \ddots & ⋮\\ ⟨u_n,v_1⟩& ⟨u_n,v_2⟩& \cdots & ⟨u_n,v_n⟩\end{array}\right)$$
再有，假设所有的二维向量都是单位向量，我们会得到：
$$G=\left(\begin{array}{cccc}\cos ({\varphi }_{1,1})& \cos ({\varphi }_{1,2})& \cdots & \cos ({\varphi }_{1,n})\\ \cos ({\varphi }_{2,1})& \cos ({\varphi }_{2,2})& \cdots & \cos ({\varphi }_{2,n})\\ ⋮& ⋮& \ddots & ⋮\\ \cos ({\varphi }_{n,1})& \cos ({\varphi }_{n,2})& \cdots & \cos ({\varphi }_{n,n})\end{array}\right)$$
其中 $\Phi (i,j)$ 是两个向量的夹角。

关键结论：为什么要用 Gram 矩阵？

Gram 矩阵保留了时间依赖性。由于时间随着位置从左上角到右下角的移动而增加，所以时间维度被编码到矩阵的几何结构中。

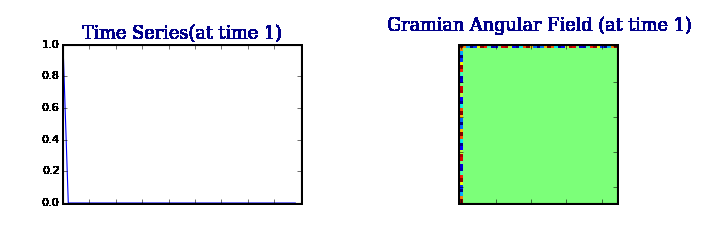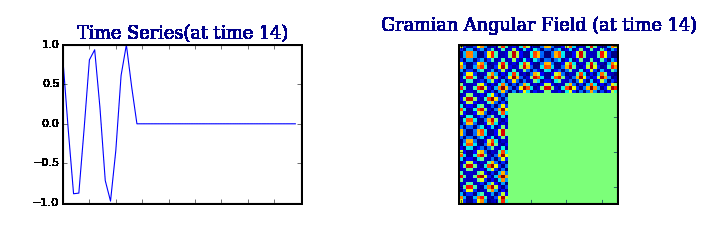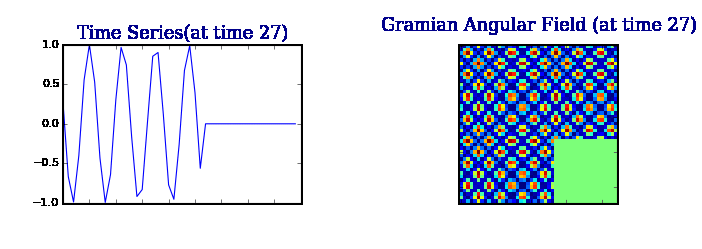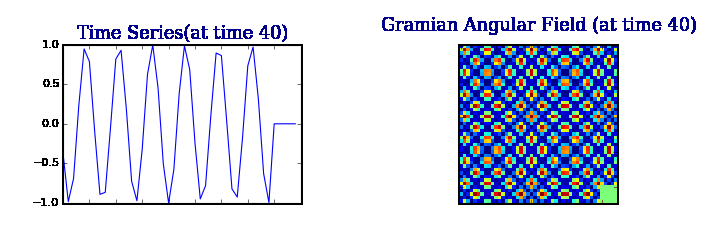
注：单变量时间序列在某种程度上无法解释数据的共现和潜在状态；我们的目标应该是找到替代的和更丰富的表示。

2. 实现方式

假设有一时间序列 $X=x_1,\cdots ,x_n$：

2.1. 缩放

使用一个限定在 [-1,1] 的最小-最大定标器（Min-Max scaler）来把时间序列缩放到 [-1,1] 里，这样做的原因是为了使内积不偏向于值最大的观测。

在这个用例中，标准缩放器 不是合适的候选者，因为它的输出范围和产生的内部积都可能超过 [- 1,1]。

然而，与最小-最大定标器结合，内积确实保留了输出范围：
$$\begin{gathered} ⟨\cdot ,\cdot ⟩:[-1,1]\times [-1,1]\to [-1,1] \\ (x,y)\to x\cdot y \end{gathered}$$
在 [-1,1] 中进行点积的选择并不是无害的。如非必要，把 [-1,1] 作为输入范围是非常可取的。

2.2. 噪声图片

缩放完时间序列之后，我们计算每一对的点积并把它们放进 Gram 矩阵里：
$$G=\left(\begin{array}{cccc}{x}_1\cdot x_1& x_1\cdot x_2& \cdots & x_1\cdot x_n\\ x_2\cdot x_1& x_2\cdot x_2& \cdots & x_2\cdot x_n\\ ⋮& ⋮& \ddots & ⋮\\ x_n\cdot x_1& x_n\cdot x_2& \cdots & x_n\cdot x_n\end{array}\right)$$

我们查看一下 G 的值来看一下这个图片：

可以看到：

1. 输出似乎遵循以 0 为中心的高斯分布。

2. 得到的图片是有噪声的。

前者解释了后者，因为数据的高斯分布越多，就越难将其与高斯噪声区分开来。

这对我们的神经网络来说是个问题。此外，CNN 在处理稀疏数据方面表现更好（CNN work better with sparse data）已经得到证实。

2.3. 非稀疏性

高斯分布并不奇怪。当看三维内积值 $z$ 的图像，对所有 $(x,y)\in R^{²}$ 的可能的组合,我们得到一个点积的三位表面：

假设时间序列的值服从均匀分布 [-1,1]，则矩阵的值服从高斯分布。下面是长度为 n 的不同时间序列的 Gram 矩阵值输出的直方图：

3. 开始编码

由于单变量时间序列是一维的，点积不能区分有价值的信息和高斯噪声，除了改变空间，没有其他利用「角」关系的方法。

因此，在使用类似于 Gram 矩阵的构造之前，我们必须将时间序列编码为至少二维的空间。为此，我们将在一维时间序列和二维空间之间构造一个双射映射，这样就不会丢失任何信息。

这种编码很大程度上是受到极坐标转换的启发，但是在这种情况下，半径坐标表示时间。

3.1. 缩放序列

第一步：用 Min-Max scaler 把序列缩放到 [-1,1] 上

我们的过程与上面实现方式中类似。加上 Min-Max scaler，我们的极坐标编码将是双射的，使用 $arccos$函数双射（参见下一步)。

第二步：将缩放后的时间序列转换到「极坐标」

需要考虑两个量，时间序列的值及其对应的时间戳。这两个变量分别用角度和半径表示。

假设我们的时间序列由 $N$ 个时间戳 $t$ 和对应的 $x$ 组成，那么:

• 角度是用 $arccos(x)$ 计算的，值在 $[0,\pi ]$ 之间。
• 首先计算半径变量，我们把区间 [0,1] 分成 $N$ 等份。因此，我们得到 $N+1$ 个分隔点 $\{0,\cdots ,1\}$ 。然后我们丢弃 0，并连续地将这些点与时间序列关联起来。

数学定义为：
$$\{\begin{array}{l}{\varphi }_i=arccos(x_i)\\ r_i=\frac{i}{N}\end{array}$$
这些编码有几个优点：

1. 整个编码是双射的（作为双射函数的组合）。
2. 它通过 $r$ 坐标保持时间依赖性。这个优点很有用。

4. 时间序列的内积

在二维空间中，接下来的问题是我们如何使用内积运算来处理稀疏性。

4.1. 为什么不是极坐标编码值的内积呢？

二维极坐标空间的内积有几个限制，因为每个向量的范数都根据时间依赖性进行了调整。更准确地说应该是：

• 两个截然不同的观察结果之间的内积将偏向于最近的一个（因为范数随时间增加）；
• 当计算观测值与自身的内积时，得到的范数也是有偏差的。

因此，如果存在一个像这样的内积运算，它应该只依赖于角度。

4.2. 使用角度

由于任何类似于内积的操作都不可避免地将两个不同观测值的信息转换成一个值，所以我们不能同时保留两个角度给出的信息。我们必须做出一些让步。

为了最好地从两个角度解释个体和连接信息，作者定义了内积的另一种操作：
$$x\oplus y=\cos ({\theta }_1+{\theta }_2)$$
其中 $\theta$ 表示 $x$ 和 $y$ 的角度。

注意：我选择了不同的符号而不是使用内积，因为这个操作不满足内积的要求（线性，正定）。

这就产生了如下的类 Gram 矩阵:
$$G=\left(\begin{array}{cccc}\cos ({\varphi }_1+{\varphi }_1)& \cos ({\varphi }_1+{\varphi }_2)& \cdots & \cos ({\varphi }_1+{\varphi }_n)\\ \cos ({\varphi }_2+{\varphi }_1)& \cos ({\varphi }_2+{\varphi }_2)& \cdots & \cos ({\varphi }_2+{\varphi }_n)\\ ⋮& ⋮& \ddots & ⋮\\ \cos ({\varphi }_n+{\varphi }_1)& \cos ({\varphi }_n+{\varphi }_2)& \cdots & \cos ({\varphi }_n+{\varphi }_n)\end{array}\right)$$

作者的选择这样做的动机是：相对于笛卡尔坐标，极坐标保留绝对的时间关系。

优势

1. 对角线由缩放后的时间序列的原始值构成（我们将根据深度神经网络学习到的高层特征来近似重构时间序列）；
2. 时间相关性是通过时间间隔 $k$ 的方向叠加，用相对相关性来解释的。

4.3. 稀疏表示

现在我们来画出格拉姆角场（Gramian Angular Field）的值的密度分布：

从上图中我们可以看出，格拉姆角场要稀疏得多。为了解释这一点,让我们用 $u\oplus v$ 在笛卡尔坐标重新表示：
$$\begin{array}{ccc}\cos ({\theta }_1+{\theta }_2)& =& cos(arccos(x)+arccos(y))\\ & =& cos(acrccos(x))\cdot cos(arccos(y))-sin(arccos(x))\cdot sin(arccos(y))\\ & =& x\cdot y+\sqrt{1-x^2}\cdot \sqrt{1-y^2}\\ & =& ⟨x,y⟩-\sqrt{1-x^2}\cdot \sqrt{1-y^2}\end{array}$$
我们在上一项中注意到，新构造的运算对应于传统内积的惩罚版本：
$$x\oplus y=x\cdot y-⟩-\sqrt{1-x^2}\cdot \sqrt{1-y^2}$$
为了了解一下这种惩罚的作用。让我们先来看看整个操作的 3D 图：

可以看到：

• 惩罚将平均输出移向 -1；
• $x$ 和 $y$ 越接近0，惩罚越大。主要的原因是，这些点点更接近高斯噪声；
• 对于 $x=y$：会转换为 -1；
• 输出很容易与高斯噪声区分开。

缺点

• 主对角线,然而,生成的 GAM 很大是由于 $n\mapsto n^2$，而原始时间序列的长度为 n。作者建议通过使用分段聚合近似（Piecewise Aggregation Approximation）减少大小。
• 这个操作不是真正意义上的内积。

5. 代码

在 Github 上可以找到将单变量时间序列转换为图像的 numpy 实现。

总结：这篇博文的灵感主要来自王志光和 Tim 的一篇详细的论文，他们利用平铺的卷积神经网络将时间序列编码为图像进行视觉检查和分类。论文中还提到了另一种有趣的编码技术：马尔科夫转换域。