基本算法(C++)前缀和与差分

1、激光炸弹

题目：一种新型的激光炸弹，可以摧毁一个边长为 R 的正方形内的所有的目标。

现在地图上有 N 个目标，用整数Xi,Yi表示目标在地图上的位置，每个目标都有一个价值Wi。

激光炸弹的投放是通过卫星定位的，但其有一个缺点，就是其爆炸范围，即那个边长为 R 的正方形的边必须和x，y轴平行。

若目标位于爆破正方形的边上，该目标不会被摧毁。

求一颗炸弹最多能炸掉地图上总价值为多少的目标。

输入格式
第一行输入正整数 N 和 R ,分别代表地图上的目标数目和正方形的边长，数据用空格隔开。

接下来N行，每行输入一组数据，每组数据包括三个整数Xi,Yi,Wi,分别代表目标的x坐标，y坐标和价值，数据用空格隔开。

输出格式
输出一个正整数，代表一颗炸弹最多能炸掉地图上目标的总价值数目。

数据范围
$0<N\le 10000$
$0\le Xi,Yi\le 5000$

输入样例：
2 1
0 0 1
1 1 1
输出样例：
1

思路：二维前缀和+各种内存优化

我们首先观察题目，可以建立一个数组f[i][j]表示坐标为(xi,yj)(xi,yj)上的权值，那么我们接着思考，因为题目上面说了要求算出这个边长为r的正方形面积，而且整个题目中，只有查询操作，没有修改操作，且内存只要略微省着用，就可以满足O(n^2)的条件，所以我们可以确认这一题可以使用二维前缀和。

• 二维前缀和，顾名思义，它的意义就是，在一个二维的空间中，求取前缀和，那么不同于一维前缀和，它的特点是什么？首先，我们可以观察，$f[i][j],f[i-1][j],f[i][j-1],a[i-1][j-1]$的关系，可以通过画一个矩阵，看几何意义，就可以很容易地明白它的代数意义 ,得出$f[i][j]=f[i-1][j]+f[i][j-1]-f[i-1][j-1]+a[i][j]$。
  比如下图：
  
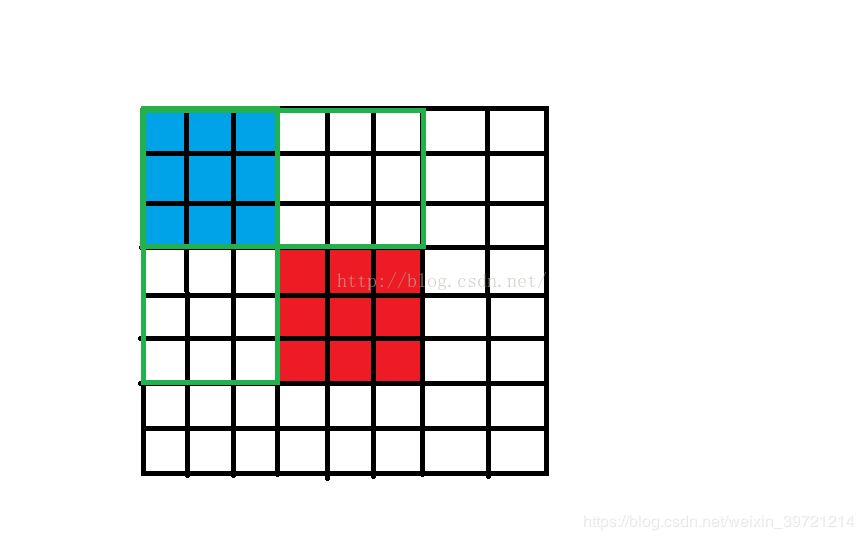
  a[i][j] 表示(0,0)到(i,j)的和。
  我们要求红色部分，就要a[i][j] - a[i - r][j] - a[i][j - r] + a[i - r][j - r]
• 内存优化手段
  你可以省略a[i][j]数组，将它用f[i][j]代替
  因为 0

注意 ：虽然矩形边上的点不会被炸，我们把(xi,yi)(xi,yi)作为一个格子,但是实际上他们只是一个点,所以说我们不妨认为这个点就是这个格子的中心,既然如此的话我们就可以认为是(xi−0.5,yi−0.5)。这样边界情况就可以排除考虑了。

代码：

#include
#include
#include

using namespace std;

const int N=5010;

int n,m;
int s[N][N];

int main(){
    int Des,R;
    cin>>Des>>R;//输入目标个数和矩形边长
    
    R=min(5001,R);//题目给的矩形大小范围，因为从1坐标开始计算，则最大坐标5001
    
    n=m=R;
    
    while(Des--){
        int x,y,w;
        cin>>x>>y>>w;
        x++,y++;
        n=max(n,x);
        m=max(m,y);
        s[x][y]+=w;
    }
    
    //预处理前缀和
    
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++)
            s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
    }
    
    int res=0;
    
    //枚举所有边长是R的矩形，枚举(i,j)为右下角
    
    for(int i=R;i<=n;i++)
        for(int j=R;j<=m;j++)
            res=max(res,s[i][j]-s[i-R][j]-s[i][j-R]+s[i-R][j-R]);
    
    
    cout<<res<<endl;
    
    return 0;
}

2、IncDec序列

题目：给定一个长度为 n 的数列 a1,a2,…,ana1,a2,…,an，每次可以选择一个区间 [l,r][l,r]，使下标在这个区间内的数都加一或者都减一。

求至少需要多少次操作才能使数列中的所有数都一样，并求出在保证最少次数的前提下，最终得到的数列可能有多少种。

输入格式
第一行输入正整数n。

接下来n行，每行输入一个整数，第i+1行的整数代表ai。

输出格式
第一行输出最少操作次数。

第二行输出最终能得到多少种结果。

数据范围
0 0≤ai<21474836480

输入样例：
4
1
1
2
2
输出样例：
1
2

思路：差分法和贪心思想

差分解决一段区域同时增加或减少的问题
给区间【L，R】上都加上一个常数c，则b[L] += c , b[R + 1] -=c

求出a的差分序列b，其中b1 = a1,b(i) = a(i) - a(i - 1) (2 <= i <= n)。令b(n + 1) = 0，题目对序列a的操作，相当于每次可以选出b1,b2…b(n + 1)中的任意两个数，一个加1，另外一个减一。目标是把b2,b3,…bn变为全0。最终得到的数列a就是由 n 个 b1 构成的

任选两个数的方法可分为四类
1、2 <= i , j <=n（优先）
2、i = 1, 2 <=j <=n
3、2 <= i <= n , j = n + 1
4、i = 1, j = n + 1（没有意义）

设b2,b3…bn中正数总和为p，负数总和的绝对值为q。首先以正负数匹配的方式尽量执行1类操作，可执行min(p,q)次。剩余|p - q|个为匹对，每个可以选与b1或b(n + 1)匹配，即执行2 或 3 类操作，共需|p - q|次

综上所诉，最少操作次数为min(p,q) + |p - q|。根据|p - q|次第2、3类操作的选择情况，能产生|p - q| + 1中不同的b1的值，即最终得到的序列a可能有|p - q| + 1 种

#include
#include

using namespace std;

typedef long long LL;

const int N=500010;

int n;
int a[N];

int main(){
    cin>>n;
    for(int i=1;i<=n;i++)cin>>a[i];
    for(int i=n;i;i--)
        a[i]=a[i]-a[i-1];//从后往前求差分序列
        
    LL pos=0,neg=0;
    
    for(int i=2;i<=n;i++)
        if(a[i]>0)pos+=a[i];
        else neg-=a[i];
        
    cout<<min(pos,neg)+abs(pos-neg)<<endl;
    cout<<abs(pos-neg)+1<<endl;
    
    return 0;
    
}

3、IncDec序列

题目：有 NN 头牛站成一行，被编队为1、2、3…N1、2、3…N，每头牛的身高都为整数。

当且仅当两头牛中间的牛身高都比它们矮时，两头牛方可看到对方。

现在，我们只知道其中最高的牛是第 PP 头，它的身高是 HH ，剩余牛的身高未知。

但是，我们还知道这群牛之中存在着 MM 对关系，每对关系都指明了某两头牛 AA 和 BB 可以相互看见。

求每头牛的身高的最大可能值是多少。

输入格式
第一行输入整数N,P,H,MN,P,H,M，数据用空格隔开。

接下来M行，每行输出两个整数 AA 和 BB ，代表牛 AA 和牛 BB 可以相互看见，数据用空格隔开。

输出格式
一共输出 NN 行数据，每行输出一个整数。

第 ii 行输出的整数代表第 ii 头牛可能的最大身高。

数据范围
1≤N≤10000,1≤H≤1000000,1≤A,B≤10000,0≤M≤10000

输入样例：
9 3 5 5
1 3
5 3
4 3
3 7
9 8
输出样例：
5
4
5
3
4
4
5
5
5

思路：差分+区间处理小操作

题目的核心就是如何处理这些特殊的关系，也就是两头牛互相看见。
其实题目中已经告诉我们如何处理，因为我们发现，题目中要求牛的身高最高，那么既然如此，我们完全可以将每一组关系(A,B)(A,B)，看作[A+1,B−1]这组牛身高只比A,BA,B这两头牛矮1. 关系如图所示

因此我们可以可以利用区间处理小操作，也就是前缀和加差分。设一个数组D，D[i]为比最高牛矮多少，则D[P]=0，那么对于一组关系，我们可以这样操作,D[A+1]–,D[B]++;然后从左到右前缀和，就可以求出矮多少。
注意：不要忘记初始化height[1]为最大值h！

代码：

#include
#include
#include

using namespace std;

int height[10010],n,p,h,m;

int main(){
    
    cin>>n>>m>>h>>m;
    
    height[1]=h;//height[1]初始化为最高的牛
    set<pair<int,int>> existed;
    
    for(int i=1;i<=m;i++){//遍历这m对看得见的牛
        int a,b;
        cin>>a>>b;
        if(a>b) swap(a,b);//这两个牛的顺序不一定从前往后排,所以要交换保证第a头牛在第b头牛前
        
        if(!existed.count({a,b}))//判断是否存在重复的牛对，不存在则继续执行操作
        {
            existed.insert({a,b});
            height[a+1]--;
            height[b]++;//{a,b}之间的牛高度全部减1操作
        }
        
    }
    
    for(int i=1;i<=n;i++){
        height[i]+=height[i-1];
        cout<<height[i]<<endl;
    }
    
    return 0;
}