指数平滑（时间序列预测）

目录

一、指数平滑

二、指数平滑详解

1、一次指数平滑（又叫简单指数平滑，simple exponential smoothing， SES）

2、二次指数平滑

3、三次指数平滑

4、平滑系数a的选择

5、指数平滑效果

---

一、指数平滑

1、定义：指数平滑法实际上是一种特殊的加权移动平均法。

指数平滑法进一步加强了观察期近期观察值对预测值的作用，对不同时间的观察值所赋予的权数不等，从而加大了近期观察值的权数，使预测值能够迅速反映市场实际的变化。权数之间按等比级数减少，此级数之首项为平滑常数a,公比为(1- a)。

指数平滑法对于观察值所赋予的权数有伸缩性，可以取不同的a 值以改变权数的变化速率。如a取小值，则权数变化较迅速，平滑作用越强，但对实际数据的变化反应迟缓。因此，运用指数平滑法，可以选择不同的a 值来调节时间序列观察值的均匀程度(即趋势变化的平稳程度)。

2、应用：

指数平滑主要用在时间序列分析，做时间序列的预测模型，时间序列具有稳定性和规则性；

3、类型：

根据平滑次数不同，指数平滑法分为一次指数平滑法、二次指数平滑法和三次指数平滑法等。但它们的基本思想都是：预测值是以前观测值的加权和，且对不同的数据给予不同的权数，新数据给予较大的权数，旧数据给予较小的权数。

二、指数平滑详解

1、一次指数平滑（又叫简单指数平滑，simple exponential smoothing， SES）

一次指数平滑实际就是对历史数据的加权平均，它可以用于任何一种没有明显函数规律但确实存在某种前后关联的时间序列的短期预测。

一次平滑计算公式为：

• 是 t 期的实际值；

一次平滑预测公式为：

• 是 t+1 期的预测值，即本期（t期）的平滑值St ；

• 是 t 期的预测值，即t-1期的平滑值 ；

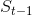简单记住：某一期的平滑值是下一期的预测值。

note：远期的实测值对未来时期平滑值的影响会越来越小，如下面的展开式：

将的表达式逐次代入中，展开整理后，得：

从上式中可以看出，一次指数平滑法实际上是以a(1 − a)k为权数的加权移动平均法。由于k越大，a(1 − a)k越小，所以越是远期的实测值对未来时期平滑值的影响就越小。 在展开式中，最后一项y1为初始平滑值，在通常情况下可用最初几个实测值的平均值来代替，或直接可用第 1 时期的实测值来代替。

 

举例1：某公司的1-11月份的销量：

月份	1	2	3	4	5
销量	3	8	10	9	未知

 

我们用一次指数平滑，预测5月份的销量。

为了分析加权系数a对平滑效果的影响，设a取值为0.2、0.8两个值，设置初始平滑值为前三个月的平均值，以a=0.8 的一次指数平滑计算为例，得：

 

 9.086

月份	1	2	3	4
销量（y）	3	8	10	9
	3.8	7.16	9.432	9.086
	6.2	6.56	7.248	7.5984

则：5月份销量的预测值在加权系数是0.2和0.8上的结果是：

             和  

（4月份的平滑值是5月份的预测值，同时a取小值，权数变化较迅速，平滑作用越强，但对实际数据的变化反应迟缓）

一次指数平滑的结论：

（1）一次指数平滑有局限性。a. 预测值不能反映趋势变动、季节波动等有规律的变动；b. 这种方法多适用于短期预测，而不适合作中长期的预测；c. 由于预测值是历史数据的均值，因此与实际序列的变化相比有滞后现象。

（2）如果序列变化比较平缓，平滑系数值应该比较小，比如小于0.l；如果序列变化比较剧烈，平滑系数值可以取得大一些，如0.3～0.5。若平滑系数值大于0.5才能跟上序列的变化，表明序列有很强的趋势，不能采用一次指数平滑进行预测。

2、二次指数平滑

二次指数平滑是对一次指数平滑的再平滑，适用于具有线性趋势的时间数列。它不能单独地进行预测，必须与一次指数平滑法配合，建立预测的数学模型，然后运用数学模型确定预测值。

二次平滑计算公式为：

• 是 t 期的实际值；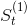
•  是第t周期的一次指数平滑值；
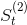•  是第t周期的二次指数平滑值；
•  是第t-1周期的二次指数平滑值；
• a 是平滑系数；

二次指数平滑的预测公式：

     （其中T是向后预测的周期）

举例2：二次指数平滑

设置一次平滑的初始值设为23，二次平滑的初始值设为28.4，以a=0.9 的一次指数平滑计算为例，得：

 

月份	1	2	3	4
销量（y）	29	36	40	48
	28.4	35.24	39.52	47.15
	28.4	34.56	39.02	46.14

 

预测第五个月的的销量，首先计算和的值：

 

预测的值，即预测未来一个周期的值，则T=1：

根据：

则：

虽然一次指数平均在产生新的数列的时候考虑了所有的历史数据，只是考虑其静态值，但没有考虑时间序列当前的变化趋势。所以二次指数平滑一方面考虑了所有的历史数据，另一方面也兼顾了时间序列的变化趋势。

3、三次指数平滑

若时间序列的变动呈现出二次曲线趋势，则需要采用三次指数平滑法进行预测。实际上是在二次指数平滑的基础上再进行一次指数平滑。它与二次指数平滑的区别就是三次平滑还考虑到了季节效应，我们需要一定的经验才能比较合理地设置其中复杂的参数。 

三次平滑计算公式为：

三次指数平滑的预测公式：

4、平滑系数a的选择

1、a值越大，实际的数据所占的比例就越大，原预测值所占比重就越小；反之，a取小值，权数变化较迅速，平滑作用越强，但对实际的数据的变化反应迟缓。

2、根据时间序列的波动大小，选择相应的a值；当时间序列波动较缓时，选择较小的a值，反之，选择较大的a值。

5、指数平滑效果

• 一次指数平滑效果

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.holtwinters import SimpleExpSmoothing

x1 = np.linspace(0, 1, 100)
y1 = pd.Series(np.multiply(x1, (x1 - 0.5)) + np.random.randn(100))
ets1 = SimpleExpSmoothing(y1)
r1 = ets1.fit()
pred1 = r1.predict(start=len(y1), end=len(y1) + len(y1)//2)

pd.DataFrame({
    'origin': y1,
    'fitted': r1.fittedvalues,
    'pred': pred1
}).plot(legend=True)
plt.tick_params(color='w')
plt.xticks(color='w')
plt.yticks(color='w')
plt.show()

 

• 二次指数平滑效果

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from statsmodels.tsa.holtwinters import Holt

x2 = np.linspace(0, 99, 100)
y2 = pd.Series(0.1 * x2 + 2 * np.random.randn(100))
ets2 = Holt(y2)
r2 = ets2.fit()
pred2 = r2.predict(start=len(y2), end=len(y2) + len(y2)//2)

pd.DataFrame({
    'origin': y2,
    'fitted': r2.fittedvalues,
    'pred': pred2
}).plot(legend=True)
plt.tick_params(color='w')
plt.xticks(color='w')
plt.yticks(color='w')
plt.show()

• 三次指数平滑效果

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from statsmodels.tsa.holtwinters import ExponentialSmoothing

x3 = np.linspace(0, 4 * np.pi, 100)
y3 = pd.Series(20 + 0.1 * np.multiply(x3, x3) + 8 * np.cos(2 * x3) + 2 * np.random.randn(100))
ets3 = ExponentialSmoothing(y3, trend='add', seasonal='add', seasonal_periods=25)
r3 = ets3.fit()
pred3 = r3.predict(start=len(y3), end=len(y3) + len(y3)//2)

pd.DataFrame({
    'origin': y3,
    'fitted': r3.fittedvalues,
    'pred': pred3
}).plot(legend=True)
plt.tick_params(color='w')
plt.xticks(color='w')
plt.yticks(color='w')
plt.show()

---

欢迎关注我的公众号，码村长实战！