机器学习-数学知识(一)
参考:《机器学习与应用》
文章目录
- 微积分与线性代数
- 导数
- 向量与矩阵
- 向量
- 代数余子式
- 伴随矩阵
- 偏导数与梯度
- 雅克比矩阵
- Hessian矩阵
- 泰勒展开
- 行列式
- 特征值与特征向量
- 奇异值分解
- 向量与矩阵求导
微积分与线性代数
导数
导数定义为函数的自变量变化值趋向于0时,函数的变化量与自变量的变化量比值的极限,即
![]()
如果上面的极限存在,则称函数在该点处可导。导数的几何意义是函数在某一点处的切线的斜率,物理意义是瞬时速度。各种基本函数和运算的求导公式

导数和函数的单调性密切相关,导数大于0时函数单调增,导数小于0时函数单调减,在极值点处导数必定为0,导数为0的点称为函数的驻点,如果对导数继续求导,得到高阶导数,二阶导数决定函数的凹凸性,如果二阶导数大于0,则函数为凸函数,如果二阶导数小于0,则为凹函数,二阶导数等于0的点称为函数的拐点。
极值判别法: 在驻点处,如果二阶导数大于0,则为函数的极小值点,如果二阶导数小于0,则为极大值点,如果二阶导数等于0,则情况不定。
向量与矩阵
向量
向量是有大小和方向的量,是由多个数构成的一维数组,每个数称为它的分量。分量的数量称为向量的维数。n维行向量x有n个分量,记为
![]()
将行向量变成列向量,向量x的转置记为 x T x^T xT, 如下对一个行向量转置为列向量
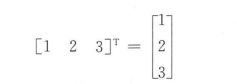
向量与标量的乘积定义为标量与向量每个分量相乘,向量之间的加法、减法、内积定义为它们对应元素分别相加、相减、乘积的和。如果两个向量的内积为0,则称它们正交,即垂直。
向量的L-P范数是一个标量,定义为:
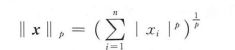
常用的是L1和L2范数,向量的L1范数为所有分量的绝对值之和,即

向量的L2范数也称为向量的模,即向量的长度,公式如下
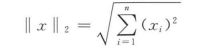
对于一组向量 x 1 , x 2 , . . . , x l x_1, x_2, ..., x_l x1,x2,...,xl,如果存在一组不全为0的数 a 1 , . . . , a l a_1, ..., a_l a1,...,al,使得
a 1 x 1 + a 2 x 2 + . . . + a l x l = 0 a_1x_1+a_2x_2+...+a_lx_l = 0 a1x1+a2x2+...+alxl=0
代数余子式
某个数的余子式是指删去那个数所在的行和列后剩下的行列式。如下图,红框部分为 a 1 a_1 a1的代数余子式

伴随矩阵
行列式 ∣ A ∣ |A| ∣A∣的各个元素的代数余子式组成的如下矩阵,称为矩阵 A A A的伴随矩阵

伴随矩阵的性质:
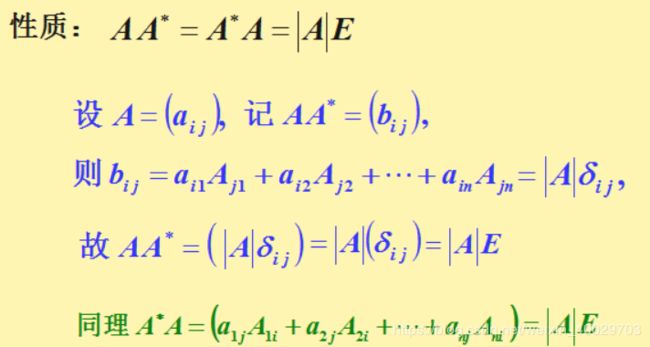
则称这组向量线性相关。如果不存在一组不全为0的数使得上式成立,则称这组向量线性无关。
对于n阶矩阵A, 如果存在n阶矩阵B, 使得他们的乘积为单位矩阵I,即
A B = I B A = I AB=I\\ BA=I AB=IBA=I
则分别称B为A的右逆矩阵和左逆矩阵。矩阵的左逆矩阵等于右逆矩阵统称为矩阵的逆,有如下公式成立:

简单可以证明上三个公式
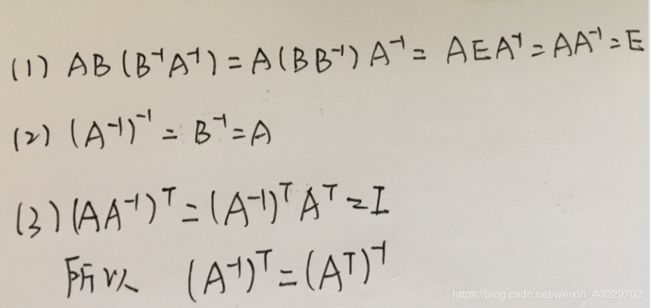
矩阵可逆的充分必要套件是其行列式不为0或者满秩
偏导数与梯度
多元函数的偏导数是一元函数导数的推广。假设有多元函数 f ( x 1 , x 2 , . . . , x n ) , 它 对 变 量 f(x_1, x_2, ..., x_n), 它对变量 f(x1,x2,...,xn),它对变量x_i$的偏导数定义为
![]()
梯度是多元函数对各自变量偏导数形成的向量。多元函数的梯度定义为

梯度和函数的单调性、极值有关。根据Fermat定理,可导函数在某一点处取得极值的必要条件是梯度为0,梯度为0的点称为函数的驻点。
雅克比矩阵
对于如下向量到向量的映射函数:
y = f ( x ) y=f(x) y=f(x)
其中,向量 x ∈ R n x\in R^n x∈Rn向量 y ∈ R n y\in R^n y∈Rn, 这个映射写成分量形式为
y i = f i ( x ) y_i=f_i(x) yi=fi(x)
即输出向量的每个分量是输入向量的函数雅克比矩阵定义为输出向量的每个分量对输入向量的每个分量的偏导数构成的矩阵:

Hessian矩阵
Hessian矩阵是由多元函数的二阶偏导数组成的矩阵。如果函数 f ( x 1 , . . . , x n ) f(x_1, ...,x_n) f(x1,...,xn)二阶可导,Hessian矩阵定义为

多元函数的混合二阶偏导数与求导次序无关,因此,Hessian矩阵是一个对称矩阵。
假设多元 函数在点M的梯度为0,即M是函数的驻点,则有以下结论:
- 如果Hessian矩阵正定,函数在该点有极小值
- 如果Hessian矩阵负定,函数在该点有极大值
- 如果Hessian矩阵不定,则不是极值点
正定矩阵:对于n阶矩阵A, 对于任意非0的n维向量x都有
x T A x > 0 x^TAx > 0 xTAx>0
则称矩阵A为正定矩阵,判定矩阵正定的常用方法有以下几种:
1)矩阵的特征值全大于0
2)矩阵的所有顺序主子式都大于0, 顺序主子式的概念
3)矩阵合同于单位阵I。合同矩阵
泰勒展开
一元函数n阶可导,它的泰勒展开式为
![]()
多元函数的泰勒展开式为
![]()
这里的O表示高阶无穷小,H是Hessian矩阵
行列式
如果矩阵A和B是尺寸相同的n阶矩阵,则有
∣ A B ∣ = ∣ A ∣ ∣ B ∣ |AB|=|A||B| ∣AB∣=∣A∣∣B∣
即矩阵乘积的行列式等于矩阵行列式的乘积。
如果矩阵可逆,则有
∣ A − 1 ∣ = ∣ A ∣ − 1 |A^{-1}|=|A|^{-1} ∣A−1∣=∣A∣−1
逆矩阵的行列式等于行列式的逆。
矩阵与标量乘法的行列式为
∣ α A = α n ∣ A ∣ |\alpha A=\alpha ^n |A| ∣αA=αn∣A∣
其中,n个矩阵的阶数
特征值与特征向量
对于一个n阶矩阵A, 如果存在一个数 λ \lambda λ和一个非0向量x,满足
A x = λ x Ax=\lambda x Ax=λx
则称 λ \lambda λ为矩阵A的特征值,x为该特征值对应的特征向量。求解如下的n次方程可以得到所有特征值
∣ A − λ I = 0 |A-\lambda I=0 ∣A−λI=0
求解特征值的经典方法是QR算法和雅克比法
根据韦达定理,矩阵所有特征值的和为矩阵的迹
∑ i = 1 n = t r ( A ) \sum ^n_{i=1}=tr(A) i=1∑n=tr(A)
矩阵所有特征值的积为矩阵的行列式
∏ λ i = ∣ A ∣ \prod \lambda_i=|A| ∏λi=∣A∣
如果n阶矩阵满足
p − 1 = p T p^{-1}=p^T p−1=pT
则称为正交矩阵。正交矩阵的行列式为1,可简单证明:

对于一个阶矩阵A,如果存在一个正交矩阵P,使得
P − 1 A P = B P^{-1}AP=B P−1AP=B
则称P为对角化旋转矩阵,其中B为对角矩阵,矩阵B的对角线元素为矩阵A的特征值,矩阵P的列为矩阵A的正交化特征向量。
奇异值分解
奇异值分解,简称为SVD, 假设A是一个 m ∗ n m*n m∗n的矩阵,则存在如下分解:
A = U Σ V T A=U\Sigma V^T A=UΣVT
其中,U是 m ∗ m m*m m∗m的正交矩阵,其列称为矩阵A的左奇异向量,U的列为 A A T AA^T AAT的特征向量, Σ \Sigma Σ 为 m ∗ n m*n m∗n的对角矩阵,V为 n ∗ n n*n n∗n 的正交矩阵,其行称为矩阵A的右奇异向量,V的列为 A T A A^TA ATA的特征向量。
向量与矩阵求导
对于如下的二次函数
f = x T A x f=x^TAx f=xTAx
其自变量为x, 展开之后写成求和形式为
f = ∑ i = 1 n ∑ j = 1 n a i j x i x j f=\sum^n_{i=1}\sum^n_{j=1}a_{ij}x_ix_j f=i=1∑nj=1∑naijxixj
从而得到梯度计算
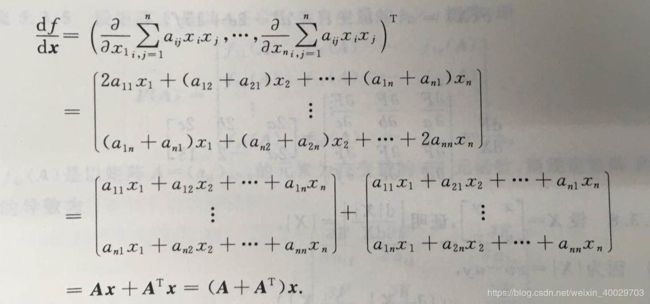
如果A是对称矩阵,上式可以简化为
▽ x T A x = 2 A x \bigtriangledown x^TAx=2Ax ▽xTAx=2Ax
参考:
- https://blog.csdn.net/u013066730/article/details/100533825
- 《机器学习与应用》雷明