六轴传感器—姿态检测(MPU6050、LSM6DS3)
1 姿态检测
1.1 Roll-pitch-yaw模型与姿态计算
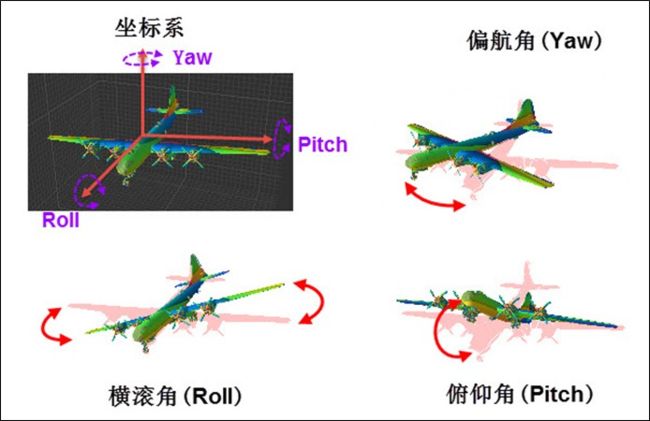
表示飞行器当前飞行姿态的一个通用模型就是建立下图所示坐标系,并用Roll表示绕X轴的旋转,Pitch表示绕Y轴的旋转,Yaw表示绕Z轴的旋转。
由于MPU6050可以获取三个轴向上的加速度,而地球重力则是长期存在且永远竖直向下,因此我们可以根据重力加速度相对于芯片的指向为参考算得当前姿态。
为方便起见,我们让芯片正面朝下固定在上图飞机上,且座标系与飞机的坐标系完全重合,以三个轴向上的加速度为分量,可构成加速度向量a(x,y,z)。假设当前芯片处于匀速直线运动状态,那么a应垂直于地面上向,即指向Z轴负方向,模长为|a|=g=sqrt{X^ 2 +Y^ 2+ z^ 2}。若芯片(座标系)发生旋转,由于加速度向量a仍然竖直向上,所以Z轴负方向将不再与a重合。见下图。
为了方便表示,上图坐标系的Z轴正方向(机腹以及芯片正面)向下,X轴正方向(飞机前进方向)向右。此时芯片的Roll角Φ(黄色)为加速度向量与其在XZ平面上投影(x,0,z)的夹角,Pitch角ω(绿色)与其在YZ平面上投影(0,y,z)的夹角。求两个向量的夹角可用点乘公式:![]() ,简单推导可得:
,简单推导可得:
注意,因为arccos函数只能返回正值角度,因此还需要根据不同情况来取角度的正负值。当y值为正时,Roll角要取负值,当x轴为负时,Pitch角要取负值。
1.2 Yaw角的问题
因为没有参考量,所以无法求出当前的Yaw角的绝对角度,只能得到Yaw的变化量,也就是角速度GYR_Z。当然,我们可以通过对GYR_Z积分的方法来推算当前Yaw角(以初始值为准),但由于测量精度的问题,推算值会发生漂移,一段时间后就完全失去意义了。然而在大多数应用中,比如无人机,只需要获得GRY_Z就可以了。
如果必须要获得绝对的Yaw角,那么应当选用MPU9250这款九轴运动跟踪芯片,它可以提供额外的三轴罗盘数据,这样我们就可以根据地球磁场方向来计算Yaw角了,具体方法此处不再赘述。
2 MPU-6050
1、16位的ADC,每个轴输出的数据,是2^16 也就是 -32768 — +32768
2、高达 400kHz 快速模式的 I2C,或最高至 20MHz 的 SPI 串行主机接口
2.1 陀螺仪灵敏度
| 可测范围 dps | 灵敏度 LSB |
|---|---|
| ±250 | 131 |
| ±500 | 65.5 |
| ±1000 | 32.8 |
| ±2000 | 16.4 |
设置了是 ±250 , 那么-32768 —- +32768 就代表了 -250 — +250
角速度数据 = (pi/180) * 轴原始数据 / 加速度灵敏度 (rad/s)
Data=数据高八位<<8|数据低八位;
Pi=3.1415926;
Ω=(pi/180)*Data/16.4 (rad/s)
2.2 加速度灵敏度
| 可测范围 g | 灵敏度LSB |
|---|---|
| ±2 | 16384 |
| ±4 | 8192 |
| ±8 | 4096 |
| ±16 | 2048 |
加速度数据 = 轴原始数据 / 加速度灵敏度
Data=数据高八位<<8|数据低八位;
A=9.8*Data/2048 (m/s^2)
3 LSM6DS3
3.1 加速度
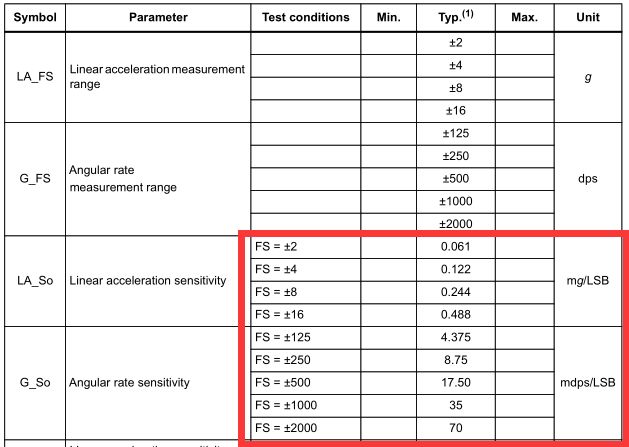
加速度数据 = 轴原始数据 * Typ / 1000
如±2g,则 加速度数据= 轴原始数据 * 0.061 (切换单位为mg)/ 1000(切换单位为g)
换算下就是:
加速度数据 = 轴原始数据 / 加速度灵敏度
| 可测范围 g | 灵敏度LSB |
|---|---|
| ±2 | 16393.44 |
| ±4 | 8196.72 |
| ±8 | 4098.36 |
| ±16 | 2049.18 |
3.2 陀螺仪
*角速度数据 = (pi/180) 轴原始数据 * Typ / 1000
如±125,则 加速度数据= (pi/180) * 轴原始数据 * 4.375 (切换单位为mbps)/ 1000(切换单位为bps)
换算下就是:
*角速度数据 = (pi/180) 轴原始数据 / 加速度灵敏度
| 可测范围 dps | 灵敏度 LSB |
|---|---|
| ±125 | 228.57 |
| ±250 | 114.29 |
| ±500 | 57.14 |
| ±1000 | 28.57 |
| ±2000 | 14.29 |
校准
校准是比较简单的工作,我们只需要找出摆动的数据围绕的中心点即可。我们以GRY_X为例,在芯片处理静止状态时,这个读数理论上讲应当为0,但它往往会存在偏移量,比如我们以10ms的间隔读取了10个值如下:
-158.4, -172.9, -134.2, -155.1, -131.2, -146.8, -173.1, -188.6, -142.7, -179.5
这10个值的均值,也就是这个读数的偏移量GRY_X0为-158.25。在获取偏移量后,每次的读数都减去偏移量就可以得到校准后的读数了。当然这个偏移量只是估计值,比较准确的偏移量要对大量的数据进行统计才能获知,数据量越大越准,但统计的时间也就越慢。一般校准可以在每次启动系统时进行,那么你应当在准确度和启动时间之间做一个权衡。
算法求欧拉角
四元数法
可通过软件实现,六个数据转化成四元数(q0、q1、q2、q3),然后四元数转化成欧拉角(P、R、Y 角)
芯片自身也带这个功能,通过配置DMP可以快速获取欧拉角(P、R、Y 角)
// 变量定义
#define Kp 100.0f // 比例增益支配率收敛到加速度计/磁强计
#define Ki 0.002f // 积分增益支配率的陀螺仪偏见的衔接
#define halfT 0.001f // 采样周期的一半
float q0 = 1, q1 = 0, q2 = 0, q3 = 0; // 四元数的元素,代表估计方向
float exInt = 0, eyInt = 0, ezInt = 0; // 按比例缩小积分误差
float Yaw,Pitch,Roll; //偏航角,俯仰角,翻滚角
//加速度单位g,陀螺仪rad/s
void IMUupdate(float gx, float gy, float gz, float ax, float ay, float az)
{
float norm;
float vx, vy, vz;
float ex, ey, ez;
// 测量正常化
norm = sqrt(ax*ax + ay*ay + az*az);
ax = ax / norm; //单位化
ay = ay / norm;
az = az / norm;
// 估计方向的重力
vx = 2*(q1*q3 - q0*q2);
vy = 2*(q0*q1 + q2*q3);
vz = q0*q0 - q1*q1 - q2*q2 + q3*q3;
// 错误的领域和方向传感器测量参考方向之间的交叉乘积的总和
ex = (ay*vz - az*vy);
ey = (az*vx - ax*vz);
ez = (ax*vy - ay*vx);
// 积分误差比例积分增益
exInt = exInt + ex*Ki;
eyInt = eyInt + ey*Ki;
ezInt = ezInt + ez*Ki;
// 调整后的陀螺仪测量
gx = gx + Kp*ex + exInt;
gy = gy + Kp*ey + eyInt;
gz = gz + Kp*ez + ezInt;
// 整合四元数率和正常化
q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT;
q1 = q1 + (q0*gx + q2*gz - q3*gy)*halfT;
q2 = q2 + (q0*gy - q1*gz + q3*gx)*halfT;
q3 = q3 + (q0*gz + q1*gy - q2*gx)*halfT;
// 正常化四元
norm = sqrt(q0*q0 + q1*q1 + q2*q2 + q3*q3);
q0 = q0 / norm;
q1 = q1 / norm;
q2 = q2 / norm;
q3 = q3 / norm;
Pitch = asin(-2 * q1 * q3 + 2 * q0* q2)* 57.3; // pitch ,转换为度数
Roll = atan2(2 * q2 * q3 + 2 * q0 * q1, -2 * q1 * q1 - 2 * q2* q2 + 1)* 57.3; // rollv
//Yaw = atan2(2*(q1*q2 + q0*q3),q0*q0+q1*q1-q2*q2-q3*q3) * 57.3; //偏移太大,等我找一个好用的
}