机器学习之过拟合欠拟合

机器学习之过拟合，欠拟合

过拟合现象是指当我们能够提高训练集上的表现时，然而测试集的表现很差，例如在深度学习中经常训练集达到99以上而数据集却在50,60左右明显过拟合，此时就要想办法阻止过拟合，过拟合也成为过配。

过拟合发生的本质原因，是由于监督学习问题的不适定：在高中数学我们知道，从n个（线性无关）方程可以解n个变量，解n+1个变量就会解不出。在监督学习中，往往数据（对应了方程）远远少于模型空间（对应了变量）。因此过拟合现象的发生，可以分解成以下三点：

1. 有限的训练数据不能完全反映出一个模型的好坏，然而我们却不得不在这有限的数据上挑选模型，因此我们完全有可能挑选到在训练数据上表现很好而在测试数据上表现很差的模型，因为我们完全无法知道模型在测试数据上的表现。
2. 如果模型空间很大，也就是有很多很多模型可以给我们挑选，那么挑到对的模型的机会就会很小。
3. 与此同时，如果我们要在训练数据上表现良好，最为直接的方法就是要在足够大的模型空间中挑选模型，否则如果模型空间很小，就不存在能够拟合数据很好的模型。

由上3点可见，要拟合训练数据，就要足够大的模型空间；用了足够大的模型空间，挑选到测试性能好的模型的概率就会下降。因此，就会出现训练数据拟合越好，测试性能越差的过拟合现象。

过拟合的解决方案：

1、交叉检验，通过交叉检验得到较优的模型参数;
2、特征选择，减少特征数或使用较少的特征组合，对于按区间离散化的特征，增大划分的区间;
3、正则化，常用的有 L1、L2 正则。而且 L1正则还可以自动进行特征选择;
4、如果有正则项则可以考虑增大正则项参数 lambda;
5、增加训练数据可以有限的避免过拟合;
6、Bagging ,将多个弱学习器Bagging 一下效果会好很多，比如随机森林等.

在深度神经网络模型训练中的解决方案：

1，增加数据量，可以通过数据增强的方法增加，随机裁剪翻转，抖动。。

2，早停策略。本质上是交叉验证策略，选择合适的训练次数，避免训练的网络过度拟合训练数据。
3，集成学习策略。而DNN可以用Bagging的思路来正则化。首先我们要对原始的m个训练样本进行有放回随机采样，构建N组m个样本的数据集，然后分别用这N组数据集去训练我们的DNN。即采用我们的前向传播算法和反向传播算法得到N个DNN模型的W,b参数组合，最后对N个DNN模型的输出用加权平均法或者投票法决定最终输出。不过用集成学习Bagging的方法有一个问题，就是我们的DNN模型本来就比较复杂，参数很多。现在又变成了N个DNN模型，这样参数又增加了N倍，从而导致训练这样的网络要花更加多的时间和空间。因此一般N的个数不能太多，比如5-10个就可以了。
4，DropOut策略。所谓的Dropout指的是在用前向传播算法和反向传播算法训练DNN模型时，一批数据迭代时，随机的从全连接DNN网络中去掉一部分隐藏层的神经元。在对训练集中的一批数据进行训练时，我们随机去掉一部分隐藏层的神经元，并用去掉隐藏层的神经元的网络来拟合我们的一批训练数据。使用基于dropout的正则化比基于bagging的正则化简单，这显而易见，当然天下没有免费的午餐，由于dropout会将原始数据分批迭代，因此原始数据集最好较大，否则模型可能会欠拟合。

5，添加正则化

欠拟合解决方案：

1、增加新特征，可以考虑加入进特征组合、高次特征，来增大假设空间;
2、尝试非线性模型，比如核SVM 、决策树、DNN等模型;
3、如果有正则项可以减小正则项参数 ;
4、Boosting ,Boosting 往往会有较小的 Bias，比如 Gradient Boosting 等.

（1、添加其他特征项，有时候我们模型出现欠拟合的时候是因为特征项不够导致的，可以添加其他特征项来很好地解决。例如，“组合”、“泛化”、“相关性”三类特征是特征添加的重要手段，无论在什么场景，都可以照葫芦画瓢，总会得到意想不到的效果。除上面的特征之外，“上下文特征”、“平台特征”等等，都可以作为特征添加的首选项。

2、添加多项式特征，这个在机器学习算法里面用的很普遍，例如将线性模型通过添加二次项或者三次项使模型泛化能力更强。例如上面的图片的例子。

3、减少正则化参数，正则化的目的是用来防止过拟合的，但是现在模型出现了欠拟合，则需要减少正则化参数。）

L1和L2正则化方法

在这些方法中，重点讲解一下L1和L2正则化方法。L1正则化和L2正则化原理类似，二者的作用却有所不同。 
（1） L1正则项会产生稀疏解。 
（2） L2正则项会产生比较小的解。 
在Matlab的DeepLearn-Toolbox中，仅实现了L2正则项。而在Keras中，则包含了L1和L2的正则项。

假如我们的每个样本的损失函数是均方差损失函数,则所有的m个样本的损失函数为：

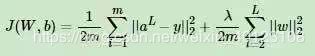
而DNN的L2正则化通常的做法是只针对与线性系数矩阵W,而不针对偏倚系数b。利用我们之前的机器学习的知识，我们很容易可以写出DNN的L2正则化的损失函数。

如果使用上式的损失函数，进行反向传播算法时，流程和没有正则化的反向传播算法完全一样，区别仅仅在于进行梯度下降法时，W的更新公式。回想我们在深度神经网络（DNN）反向传播算法(BP)中，W的梯度下降更新公式为：

则加入L2正则化以后，迭代更新公式变成：

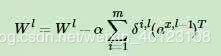
注意到上式中的梯度计算中m我忽略了，因为α是常数，而除以m也是常数，所以等同于用了新常数α来代替αm。进而简化表达式，但是不影响损失算法。类似的L2正则化方法可以用于交叉熵损失函数或者其他的DNN损失函数，这里就不累述了。

对于L1正则项，不同之处仅在于迭代更新公式中的后一项。将其改为1范数的导数即可。而一范数的导数即sign(x)，即将后一项改为sign(W)即可。

为什么PCA不推荐要用来避免过拟合

PCA最大的“问题”，就在于它是无监督的。

PCA是高维环境下能想到的最直接的方案。比如人脸识别，维度往往成千上万，但识别身份的话，每个人样本最多也就几十，过拟合现象是很严重的。由此产生了人脸识别早期研究中影响力极大的工作eigenface，其实就是先用PCA对人脸图像进行降维，然后再训练分类器。

但PCA是无监督的，正如Andrew所说：“it does not consider the values of our results y”。所以它虽然能解决过拟合问题，但又会带来欠拟合问题。拿人脸识别来说，eigenface虽然能训练出识别能力尚可的分类器，但因为分类信息并不一定存在于前几个主成分上，所以用前几个主成分来做分类的话，会丢失后面变化细微的主成分上存在的大量分类信息。正因为如此，之后又出现了fisherface等有监督降维工作，识别能力也因此提高了很多。

深度学习也是这样，pre-training阶段很多训练都是无监督的，其实和PCA异曲同工，但之后一定要有进一步的fine-tuning，把无监督提取出来的特征transfer到我们的目标任务上，这样得到的特征才真正work。

所以说，类似于PCA和auto-encoder这样的无监督方法，提取的特征不会太差、但也不会太好，它最大的作用，是总结出一些关于X的较高层次的抽象知识、为之后的有监督训练提供一个比原始特征空间更好的起点。实际上，无监督最具优势之处，就在于它的通用性：不管y是什么，只要有X就行，之后可以在各种各样的y上进一步训练。有证据显示，人类在婴儿时期也是先有一个无监督学习阶段，然后才是各种有监督学习。