数据挖掘读书笔记--第八章(下)：分类：模型评估与选择、提高分类器准确率技术

散记知识点

——“评估分类器，提高分类器”

---

5. 模型评估与选择

5.1 评估分类器性能

(1) 评估分类器性能的度量

评估分类器性能的度量主要有：准确率（识别率）、敏感度（召回率(recall)）、特效性、精度(precision)、 F1 F 1 和 Fβ F β 。

假定 P P 为正元组数、 N N 为负元组数，则下图为各种度量的计算公式：

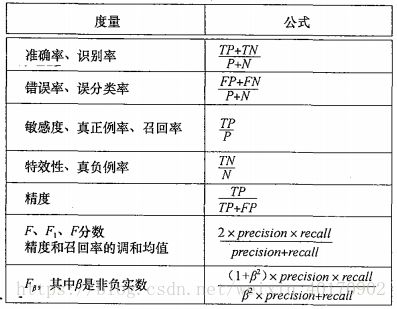
其中：

• TP T P (True Positive) 真正例：是指被分类器正确分类的正元组个数。
• TN T N (True Negative) 真负例：是指被分类器正确分类的负元组个数。
• FP F P (False Postive) 假正例：是指被错误地标记为正元组的负元组个数。
• FN F N (False Negative) 假负例：是指被错误地标记为负元组的正元组个数。

一个二分类问题的混淆矩阵:

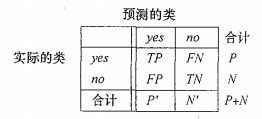
其中， P′ P ′ 表示被分类器标记为正的元组数 (TP+FP) ( T P + F P ) ； N′ N ′ 表示被分类器标记为负的元组数$(TN+FN)。

下面分别考虑每个度量指标的意义：

① 准确率
分类器在给定测试集上的准确率(accuracy)是被该分类器正确分类的元组所占的百分比：

accuracy=TP+TNP+N a c c u r a c y = T P + T N P + N

准确率又称识别率，下表显示了混淆矩阵每类及总体识别率：

观察混淆矩阵，可以看出相应的分类器是否混淆了两类。当 类分布相对平衡时，准确率是评价分类器最有效的指标。

② 灵敏度和特效性

考虑类不平衡问题，即感兴趣的类（正例）很稀少的情况，准确率会不太可靠。例如，医疗数据中，类标签为癌症”cancer”，可以分为两类：得癌症”yes”和不得癌症”no”。假设正常训练一个分类器，准确率为97%，看似很高但实际上意义却不大，因为准确率很大部分由负例”no”决定，而我们感兴趣的正例”yes”却可能没正确地被识别出来，分类器得不到我们想要的结果。
针对这个问题，使用灵敏度和特效性：
灵敏度(sensitivity)为真正例识别率即正确识别正元组的百分比：

sensitivity=TPP s e n s i t i v i t y = T P P

特效性(specifictiy)为真负例率即正确识别的负元组百分比：

specifictiy=TNN s p e c i f i c t i y = T N N

考虑一个类分布不平衡问题cancer:{‘yes’, ‘no’}，混淆矩阵为：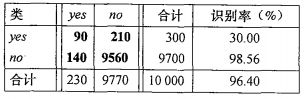

观察混淆矩阵，负例‘no’占比很大，假负例即有癌症‘yes’被判为没有癌症’no’占比很大。进一步计算该分类器的灵敏度为 90/300=30.00% 90 / 300 = 30.00 % ，特效性为 9650/9700=98.56% 9650 / 9700 = 98.56 % 。虽然总体识别率很高，但正例‘yes’的识别率灵敏度很低仅为30%，可以看出该分类器并不能准确地识别癌症。

③ 精度和召回率

精度(precision)可以看作精确性的度量即标记为正类的元组实际为正类所占的百分比：

precision=TPTP+FP p r e c i s i o n = T P T P + F P

召回率(recall)是 完全性度量即正例元组标记为正的百分比(亦称灵敏度)：

recall=TPTP+FN=TPP r e c a l l = T P T P + F N = T P P

对②中混淆矩阵计算：分类器的精度为 90/230=39.13% 90 / 230 = 39.13 % ，召回率为 90/300=30.00% 90 / 300 = 30.00 % 。

精度和召回率通常一起使用，用固定的召回率比较精度，或用固定的精度比较召回率。例如，可在75%的召回率水平比较精度。

④ Fβ F β 度量

Fβ F β 度量将精度和召回率组合到一起：

Fβ=(1+β2)×precision×recallβ2×precision+recall F β = ( 1 + β 2 ) × p r e c i s i o n × r e c a l l β 2 × p r e c i s i o n + r e c a l l

其中， β β 为非负实数，当 β=1 β = 1 时，称为 F F 度量是精度和召回率的调和平均值。 Fβ F β 是精度和召回率加权度量，赋予召回率的权重是精度的 β β 倍。通常使用 F2、F0.5 F 2 、 F 0.5

总结：当数据类比较均匀地分布时，准确率效果最好。而其他度量，如灵敏度（召回率(recall)）、特效性、精度(precision)、 F1 F 1 和 Fβ F β 更适合类不平衡问题。

(2) 其他方面评价分类器性能

除了基于度量评价分类器性能之外，还可以根据其他方面比较分类器：速度、鲁棒性、可伸缩性、可解释性等

---

5.2 划分数据集与选择分类器模型

(1) 保持法和随机二次抽样

• 保持法(holdout)：随机划分数据集为两个集合：训练集和测试集，通常大小为2:1，使用训练集导出模型，使用测试集评估模型。
• 随机二次抽样(random subsampling)：将保持法重复 k k 次，总准确率估计取每次迭代准确率的平均值。

(2) 交叉验证

k-折交叉验证(k-fold cross-validation)：

• 初始将数据集随机地划分为大小大致相等的 k k 个互不相交的子集（”折”）： D1,D2,...,Dk D 1 , D 2 , . . . , D k
• 训练和测试 k k 次，依次从 k k 子集中选择1个作为测试集，其余作为训练集。例，第1次选择 D1 D 1 作为测试集 D2∼Dk D 2 ∼ D k 为训练集。
• 准确率估计是 k k 次迭代正确分类的元组总数除以初始数据元组总数。

留一(leave-one-out)是 k k -折交叉验证的特殊情况，每次只给测试集“留出”一个样本。

一般采取10-折交叉验证估计准确率。

(3) 自助法

• 自助法(bootstrap)：从给定的训练集中有放回的均匀抽样。

• .632自助法：

  • 假设数据集包含 d d 个元组，有放回地抽取 d d 次，产生 d d 个样本的自助样本集（训练集）。
  • 原始数据元组中，某些元组可能多次出现，而从来没有出现的元组最终构成测试集。
  • 结果是，平均情况下会有：63.2%的原数据元组将会出现在训练集中，而其余的36.8%的元组将形成测试集。

之所以会是0.632，是因为每个元组被抽中的概率为 1/d 1 / d ，因此到最后都未被选中的概率为 (1−1/d)d ( 1 − 1 / d ) d 。当 d d 很大时，求极限结果近似为 e−1=0.368 e − 1 = 0.368 。因此，36.8%未被选中的元组将形成测试集，其余63.2%的元组形成训练集。

重复迭代过程 k k 次，每次得到测试集和训练集的准确率分别为 Acc(Mi)test_set、Acc(Mi)train_set A c c ( M i ) t e s t _ s e t 、 A c c ( M i ) t r a i n _ s e t ，则模型的总体准确率为：

Acc(M)=∑i=1k(0.632×Acc(Mi)test_set+0.368×Acc(Mi)train_set) A c c ( M ) = ∑ i = 1 k ( 0.632 × A c c ( M i ) t e s t _ s e t + 0.368 × A c c ( M i ) t r a i n _ s e t )

(4) 使用统计显著性检验选择模型

假设在数据集上产生2个分类模型 M1 M 1 和 M2 M 2 ，经过10折交叉验证分别得到平均错误率。为了确定两个模型的平均错误率是否存在“真正的”差别，则需要使用统计显著性检验。

• 对于给定的模型，在交叉验证中计算每个错误率都可以看作来自一种概率分布的不同的独立样本。一般地，它们服从具有 k−1(k=10) k − 1 ( k = 10 ) 自由度的 t t 分布
• 做假设检验，假设这两个模型相同即平均错误率之差为0。如果我们能够拒绝该假设，则可以断言两个模型之间的差时统计显著的。在此情况下，可以选择具有较低错误率的模型。
• 对于10折交叉验证，假设第 i i 轮， M1和M2 M 1 和 M 2 的错误率分别为 err(M1)i e r r ( M 1 ) i 和 err(M2)i e r r ( M 2 ) i 。二者的平均错误率分别为： err¯¯¯¯¯¯¯(M1) e r r ¯ ( M 1 ) 和 err¯¯¯¯¯¯¯(M2) e r r ¯ ( M 2 ) ，两个模型差的方差记为： var(M1−M2) v a r ( M 1 − M 2 )
  ,则计算 t t 统计量：
  t=err¯¯¯¯¯¯¯(M1)−err¯¯¯¯¯¯¯(M2)var(M1−M2)/k−−−−−−−−−−−−−√ t = e r r ¯ ( M 1 ) − e r r ¯ ( M 2 ) v a r ( M 1 − M 2 ) / k
  ，其中
  var(M1−M2)=1k∑i=1k[(err(M1)i−err(M2)i)−(err¯¯¯¯¯¯¯(M1)−err¯¯¯¯¯¯¯(M2))]2 v a r ( M 1 − M 2 ) = 1 k ∑ i = 1 k [ ( e r r ( M 1 ) i − e r r ( M 2 ) i ) − ( e r r ¯ ( M 1 ) − e r r ¯ ( M 2 ) ) ] 2
  
  为了确定 M1 M 1 和 M2 M 2 是否显著不同，计算 t t 并选择显著性水平 sig s i g (一般取1%或5%)。然后查找 t t -分布表。例如，要确定二者之差对总体的95%是否显著性不同，则寻找 z=sig/2=0.025 z = s i g / 2 = 0.025 的表值， z z 为置信界。如果计算所得 t t 在 t>z或t<−z t > z 或 t < − z 的拒绝域。则意味着我们可以拒绝原假设，并断言两个模型之间存在统计显著的差别。否则，不能拒绝原假设，断言二者之间的差可能随机的。

(5) 基于成本效益和ROC曲线比较分类器

真正例、真负例、假正例和假负例也可以用于评估与分类模型相关联的成本效益。与假负例相关联的代价比与真正例相关联的代价大得多。例如，错误地预测癌症患者未患癌症的代价远比保守地将未患癌症预测为癌症患者大得多。这种情况下，通过赋予每种错误不同的代价，可以使一种模型的错误比另一种更重要。

作为选择，通过计算每种决策的平均成本（或效益），可以考虑成本效益。

接收者操作特征(Receiver Operating Characteristic , ROC)曲线是一种比较分类器模型有用的可视化工具。ROC曲线显示了给定模型的真正例率( TPR=TP/P T P R = T P / P )和假正例率( FPR=FP/N F P R = F P / N )之间的权衡。TPR的增加以FPR的增加为代价。ROC曲线下方的面积是模型准确率的度量。

绘制ROC曲线：

• ROC曲线的纵轴表示TPR，横轴表示FPR。从(0, 0)开始绘制。依次从列表顶部向下检查元组的实际类标号。
• 如果元组为真正例元组，则TP增加，从而TPR增加。在图中向上移动并绘制一个点。
• 如果元组为假正例元组，则FP增加，从而FPR增加。在图中向右移动并绘制一个点。

下图为一个概率分类器对10个检验元组返回的概率值，按概率递减排列。

从元组1开始，取该元组得分为阈值即 t=0.9 t = 0.9 。则这样分类器认为元组1为正，而其他9元组为负。扫描10个元组对照元组实际类别(第二列)，可得 TP=1, FP=0 TN=5 FN=4 T P = 1 ,   F P = 0   T N = 5   F N = 4 ，因此计算得 TPR=TP/P=0.2,FPR=0 T P R = T P / P = 0.2 , F P R = 0 ，绘制一个点(0.2, 0)。继续取第二个元组得分为阈值即 t=0.8 t = 0.8 ，重复执行上述操作。结果产生10个点，据此绘制ROC曲线。如下图所示：

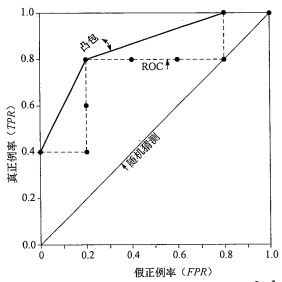
比较两个分类模型的ROC曲线：

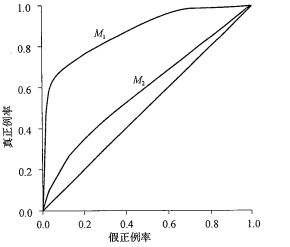
模型的ROC曲线离对角线越近，模型的准确率越低。如果模型很好，则随着有序列表向下移动，开始会遇到真正例，曲线表现为陡峭地从0上升。后来遇到的的真正例越来越少，假正例越来越多，曲线趋于水平。

---

6. 提高分类准确率技术

组合分类器(ensemble)是一个复合模型，由多个分类器组合而成。个体分类器组合，组合分类器基于投票返回类标号预测。组合分类器往往比它的成员分类器更准确。

6.1 组合分类方法简介

常见的组合分类方法主要有装袋(Bagging)、融合(stacking)、提升(Adaboost)和随机森林。组合分类把 k k 个学习得到的分类器模型 M1,M2,...,Mk M 1 , M 2 , . . . , M k 组合在一起，创建一个改进的复合分类模型 M∗ M ∗ 。给定一个待分类的新数据元组，每个基分类通过返回类预测投票。
考虑一个被两个属性 x1,x2 x 1 , x 2 描述的线性二分类问题
：
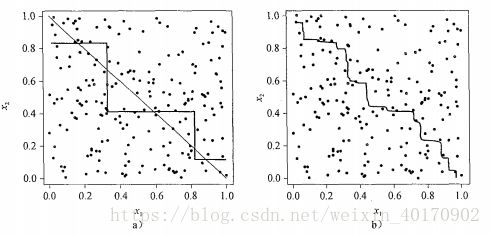
上图左是一个单决策树分类器决策边界，实际决策边界为以条直线。右图为组合决策树决策边界。尽管组合分类器的决策边界仍是分段常数，但它具有更好的解。

---

6.2 Bagging

给定数据集 D D 包含 d d 个数据元组，组合分类器数目为 k k ，Bagging**过程**如下：

• 对每次迭代 i (i=1,2,...,k) i   ( i = 1 , 2 , . . . , k ) ，采用自助法(bootstrap)，有放回地从 D D 中抽样构成训练集 Di D i 。
• 对每个训练集 Di D i ，分别学习得到分类模型 Mi M i （决策树、神经网络等）。
• 对未知分类元组 X X ，每个分类器 Mi M i 返回一个类标号（记作一票），统计票数最高的类标号赋给 X X 。

Bagging 算法如下：

• 

图解Bagging：

• 

评价：

• Bagging的准确率通常显著高于单个分类器，准确率的提高是因为复合模型降低了个体分类器的方差。另外能减少噪声和过拟合的影响，且更加鲁棒。

---

6.2 Stacking

给定训练集 D D 包含数据元组 {X1,X2,...,Xn} { X 1 , X 2 , . . . , X n } ，对应的类别（可能相同）分别为 {y1,y2,...,yn} { y 1 , y 2 , . . . , y n } ，初始训练分类器数目为 k k 个 {M1,M2,...,Mk} { M 1 , M 2 , . . . , M k } ，融合输出分类器为 M∗ M ∗ ，Stacking过程如下：

• 训练集中的每个元组 Xi X i 经过每个初始训练分类模型得到 k k 个输出 {Xi,M1,Xi,M2,...,Xi,Mk} { X i , M 1 , X i , M 2 , . . . , X i , M k } 。
• 将 k k 个输出与元组的类标号 yi y i 一起构成新的数据元组 X′i={Xi,M1,Xi,M2,...,Xi,Mk,yi} X i ′ = { X i , M 1 , X i , M 2 , . . . , X i , M k , y i } 。
• 整个每个新元组构成一个新的数据集 D′ D ′ ，训练得到融合输出分类器 M∗ M ∗ 。

Stacking 算法如下：

图解Stacking：

---

6.2 Boosting

给定原始数据集 D D ，假设训练 k k 轮，boosting一般过程如下：

• 赋予每个训练元组一个权重，迭代地学习 k k 次，每次学习得到一个分类器 Mi(i=1,2...,k) M i ( i = 1 , 2... , k ) 。
• 而在得到分类器 Mi M i 之后，更新权重，使得后面的分类器 Mi+1 M i + 1 更关注于 Mi M i 误分类的元组。
• 最终提升的分类器 M∗ M ∗ 组合每个分类器的表决，其中每个分类器投票权重是其准确率的函数。

Boosting 算法如下：

图解Boosting：

---

6.3 Adaboost

Adaboost(Adaptive Boosting) 是比较流行的提升算法。给定数据集 D D ，包含 d d 个类标记元组 (X1,y1),(X2,y2),...,(Xd,yd) ( X 1 , y 1 ) , ( X 2 , y 2 ) , . . . , ( X d , y d ) ，其中 yi y i 为类标号，Adaboost的一般过程如下：

• 开始时，Adaboost对每个训练元组赋予相等的权重 1/d 1 / d 。进行 k k 次迭代，产生 k k 个基分类器。
• 第 i i 次迭代时，从 D D 中有放回抽样形成大小为 d d 的训练集 Di D i 。每个元组被选中的机会由它的权重决定。
• 接着从训练集 Di D i 中导出分类器 Mi M i ，使用 Di D i 作为测试集计算 Mi M i 的误差。
• 如果元组被错误地分类，则增加它的权重。反之，则反之。增加权重是为着重考虑这些分类困难的元组。
• 然后，使用这些权重为下一轮的分类器产生训练样本。使其更关注上一轮误分类的元组。（某些分类器可能对某些“困难”元组分类效果更好。）

一些涉及的计算：

• ① 求模型 Mi M i 的错误率，为误分类 Di D i 中每个元组的加权和：
  error(Mi)=∑j=1dwi×err(Xj) e r r o r ( M i ) = ∑ j = 1 d w i × e r r ( X j )
  其中， err(Xj) e r r ( X j ) 是元组 Xj X j 的误分类误差：如果 Xj X j 被误分类，则 err(Xj)=1 e r r ( X j ) = 1 ；否则 err(Xj)=0 e r r ( X j ) = 0 。如果 error(Mi)>0.5 e r r o r ( M i ) > 0.5 ，则丢弃该分类器，并重新训练得到新的分类器。
• ② 更新权重，如果一个元组在第 i i 轮正确分类，则其权重乘以：
  error(Mi)/(1−error(Mi)) e r r o r ( M i ) / ( 1 − e r r o r ( M i ) )
  一旦所有正确分类元组的权重都被更新（减小），就对所有元组权重规范化：乘以旧权重之和，除以新权重之和。结果使得，误分类元组权重增加，正确分类权重减小。
• ③ 分类器 Mi M i 的表决权重：
  log1−error(Mi)error(Mi) log ⁡ 1 − e r r o r ( M i ) e r r o r ( M i )
  分类器错误率越低，准确率就越高，因此它的表决权重就应当越高。
• 使用该分类模型预测未知元组 X X 的分类时，将 X X 通过每个分类器得到一些可能的分类，同时得到 k k 个投票权重，对每个分类，计算权重和，则返回具有最大权重和的类作为 X X 的类预测

Adaboost 算法如下：

评价：与Bagging相比，Adaboost**准确率高，但是由于关注误分类元组，容易产生过拟合**。

---

6.5 随机森林

随机森林(Random Forest)是一种特殊的组合分类器，每个个体分类器都是一颗颗决策树。不同的是，这里的个体决策树在每个结点使用随机选择的属性决定划分。

随机森林可以使用Bagging与随机属性选择结合来构建，给定 d d 个训练元组的数据集 D D ，其主要构造过程如下：

• 对每次迭代 i(i=1,2,...,k) i ( i = 1 , 2 , . . . , k ) 使用自助法从 D D 有放回地抽样(Bootstrap Aggregation ) d d 次，构成训练集 Di D i 。
• 设 F F 是在每个结点决定划分数据集的属性数， F F 远小于可用属性数。
• 为构造决策树分类器 Mi M i ，在每个结点随机选择 F F 个属性作为该结点划分的候选属性。
• 使用CART算法来增长树，树增到最大规模，且不用进行剪枝。

这种使用随机输入选择形成的随机森林称为Forest-RI。

另一种形式为Forest-RC，使用输入属性的随机线性组合。

评价：

• 随机森林的准确率可以与Adaboost相媲美，但是对噪声和离群点有更好鲁棒性。
• 随着森林中树的增加，森林的泛化误差收敛，能够防止过拟合。
• 与决策树相比，不用考虑提前根据属性选择度量选择属性。
• 由于每次划分只考虑很少的属性，因此在大型数据库上非常有效。

---

6.6 拓展：探索Adaboost的数学之美

考虑初始版本Adaboost算法原理：

(1) 表决权重
在上述算法中，共有 T T 次迭代，每次迭代 t t 产生一个分类器模型 ht h t ，属于它的表决权重为：

αt=12ln(1−ϵtϵt) α t = 1 2 ln ⁡ ( 1 − ϵ t ϵ t )

每次迭代更新元组的权重分布为：

Dt+1(i)=Dt(i)Zt×{exp(−αt)    ht(xi)=yiexp(αt)    ht(xi)≠yi=Dt(i)exp(−αtyiht(xi))Zt D t + 1 ( i ) = D t ( i ) Z t × { e x p ( − α t )         h t ( x i ) = y i e x p ( α t )         h t ( x i ) ≠ y i = D t ( i ) e x p ( − α t y i h t ( x i ) ) Z t

其中， Dt(i) D t ( i ) 是上一次迭代元组的权重分布， Zt Z t 为归一化因子， yi y i 和 h(xi) h ( x i ) 为元组实际类标号和分类器类标，取值为1或-1，当二者相同时，乘积为1；不同时，乘积为-1。
输出为每个分类器的表决权重相加：

H(x)=sign(∑t=1Tαtht(x)) H ( x ) = s i g n ( ∑ t = 1 T α t h t ( x ) )

• 定理 1 ：Adaboost总分类模型的误分类误差（总体误差）error随着 Zt Z t 的最小而最小。
• 证明：
  Dt+1(i)=1m⋅e−α1yih1(xi)Zt⋅...⋅e−αTyihT(xi)ZT=e−yi∑tαtht(xi)m∏tZt=e−yif(xi)m∏tZt D t + 1 ( i ) = 1 m ⋅ e − α 1 y i h 1 ( x i ) Z t ⋅ . . . ⋅ e − α T y i h T ( x i ) Z T = e − y i ∑ t α t h t ( x i ) m ∏ t Z t = e − y i f ( x i ) m ∏ t Z t
  其中， f(xi)=∑tαtht(xi) f ( x i ) = ∑ t α t h t ( x i ) 。
• 对于元组 xi x i ，如果输出类别不是 yi y i ，则 H(xi)≠yi⇒yif(xi)⩽0⇒e−yif(xi)⩾1 H ( x i ) ≠ y i ⇒ y i f ( x i ) ⩽ 0 ⇒ e − y i f ( x i ) ⩾ 1 。
• 从而 [[H(xi)≠yi]]⩽e−yif(xi)⇒1m∑i[[H(xi)≠yi]]⩽1m∑ie−yif(xi) [ [ H ( x i ) ≠ y i ] ] ⩽ e − y i f ( x i ) ⇒ 1 m ∑ i [ [ H ( x i ) ≠ y i ] ] ⩽ 1 m ∑ i e − y i f ( x i ) 这里，模型错误率为 1m∑i[[H(xi)≠yi]] 1 m ∑ i [ [ H ( x i ) ≠ y i ] ] 。
• 继续：
  1m∑i[[H(xi)≠yi]]⩽1m∑ie−yif(xi)=∑i(∏tZt)DT+1(i)=∏tZt 1 m ∑ i [ [ H ( x i ) ≠ y i ] ] ⩽ 1 m ∑ i e − y i f ( x i ) = ∑ i ( ∏ t Z t ) D T + 1 ( i ) = ∏ t Z t
  这里 ∑iDT+1(i)=1 ∑ i D T + 1 ( i ) = 1 。
• 因此，最小化 Zt Z t ，就会最小化误差error上界:
  minαZt⇒minα∏tZt min α Z t ⇒ min α ∏ t Z t
  定理得证。

yi y i 和 h(xi) h ( x i ) 分别为元组真正分类和经过分类器模型的预测分类。 y,h(x)∈{−1,+1} y , h ( x ) ∈ { − 1 , + 1 }
Z Z 为第 t t 迭代使用的元组权重分布：

Z=∑iDie−αyih(xi) Z = ∑ i D i e − α y i h ( x i )

其中，采用概率期望思想得：

e−αyih(xi)=e−αP(yi=h(xi))+eαP(yi)≠h(xi) e − α y i h ( x i ) = e − α P ( y i = h ( x i ) ) + e α P ( y i ) ≠ h ( x i )

要取得最小值，从而最小化总体误差，对 α α 求导得：

∂Z∂α=−e−α∑iDiP(yi=h(xi))+eα∑iDiP(yi≠h(xi))=0 ∂ Z ∂ α = − e − α ∑ i D i P ( y i = h ( x i ) ) + e α ∑ i D i P ( y i ≠ h ( x i ) ) = 0

α=12ln∑iDi(1−P(yi≠h(xi)))∑iDiP(yi≠h(xi))=12ln1−ϵϵ α = 1 2 ln ⁡ ∑ i D i ( 1 − P ( y i ≠ h ( x i ) ) ) ∑ i D i P ( y i ≠ h ( x i ) ) = 1 2 ln ⁡ 1 − ϵ ϵ

其中， ϵ ϵ 表示每次迭代，单个分类器对元组的误分类误差。

(2) 误差上界

令元组权重加权和为：

r=∑iDiyih(xi) r = ∑ i D i y i h ( x i )

其中， Di D i 为每个元组的权重( ∑iDi=1 ∑ i D i = 1 )。 yi y i 和 h(xi) h ( x i ) 为元组实际类标号和分类器类标，取值为1或-1，当二者相同时，乘积为1；不同时，乘积为-1。则：

r=∑iDiyih(xi)=∑iDiP(yi=h(xi))−∑iDiP(yi≠h(xi))=∑iDi(1−P(yi≠h(xi)))−∑iDiP(yi≠h(xi))=1−2ϵ(85)(86)(87) (85) r = ∑ i D i y i h ( x i ) = ∑ i D i P ( y i = h ( x i ) ) − ∑ i D i P ( y i ≠ h ( x i ) ) (86) = ∑ i D i ( 1 − P ( y i ≠ h ( x i ) ) ) − ∑ i D i P ( y i ≠ h ( x i ) ) (87) = 1 − 2 ϵ

从而， ϵ=1−r2⇒α=12ln1+r1−r ϵ = 1 − r 2 ⇒ α = 1 2 ln ⁡ 1 + r 1 − r ，由此：

Z=∑iDie−αyih(xi)=∑iDie−(12ln1+r1−r)yih(xi)=∑iDi(1+r1−r−−−−−√)yih(xi)=∑iDi(1+r1−r−−−−−√P(yi≠h(xi))+1+r1−r−−−−−√P(yi=h(xi)))=1+r1−r−−−−−√ϵ+1+r1−r−−−−−√(1−ϵ)=11−r1−r2−−−−−√1−r2+1r+11−r2−−−−−√1+r2=1−r2−−−−−√(88)(89)(90)(91) (88) Z = ∑ i D i e − α y i h ( x i ) = ∑ i D i e − ( 1 2 ln ⁡ 1 + r 1 − r ) y i h ( x i ) = ∑ i D i ( 1 + r 1 − r ) y i h ( x i ) (89) = ∑ i D i ( 1 + r 1 − r P ( y i ≠ h ( x i ) ) + 1 + r 1 − r P ( y i = h ( x i ) ) ) (90) = 1 + r 1 − r ϵ + 1 + r 1 − r ( 1 − ϵ ) = 1 1 − r 1 − r 2 1 − r 2 + 1 r + 1 1 − r 2 1 + r 2 (91) = 1 − r 2

最终，我们得到误差上界为：

1m[[H(xi)≠yi]]≤∏tZt=∏t1−r2t−−−−−√ 1 m [ [ H ( x i ) ≠ y i ] ] ≤ ∏ t Z t = ∏ t 1 − r t 2

随着迭代次数的增加，误差上界越来越小，并越来越趋近于0。这就是Adaboost的精确的很高原因所在。