Digital Image processing 数字图像处理最佳陷波滤波器设计（频域）

最佳陷波滤波器（傅里叶变换，matlab实现）

1基本概念

1.1频域滤波步骤小结
在频域中的滤波是简单明了的。它包含如下步骤：
（1）给定一幅大小为MN的输入图像f(x,y),选择填充参数P，Q，典型地，我们选择P=2M和Q=2N。
（2）对f(x,y)添加必要数量的0，形成大小为PQ的填充后的图像fp(x,y)。
（3）用(-1)x+y乘以fp(x,y)移到其变换的中心。
（4）计算来自步骤3的图像DFT，得到F(u,v)。
（5）生成一个实的、对称的滤波函数H(u,v),其大小为PQ，中心在(P/2,Q/2)处。用阵列相乘形成乘积G(u,v)=H(u,v)F(u,v);
（6）得到处理后的图像：
（7）通过从gp(x,y)的左上象限提取MN区域，得到最终处理结果g(x,y)。
参照课本p264进行实验，如图1所示，详细可见程序filtPro.m。

1.2带阻滤波器
理想带阻滤波器的表达式为：

其中，D(u,v)是到中心化频率矩形原点的距离，W是频带的宽度，D0是频带的中心半径。
同样，n阶的巴特沃斯带阻滤波器的表达式为：

高斯带阻滤波器的表达式为：

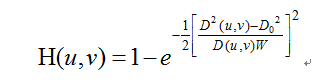
详细可见程序lowpfilter.m,参考课本p336利用带阻滤波器消除周期性噪声，如图4所示，具体代码可见filtCircle.m.

1.3带通滤波器
带通滤波器执行与带阻滤波器相反的操作。带通滤波器的传递函数Hbp(u,v)是根据相应的带阻滤波器的传递函数Hbr(u,v)并应用下式：

1.4陷波滤波器
陷波滤波器阻止（或通过）事先定义的中心频率领域内的频率。假定频率矩形的中心已经移动到点（M/2，N/2），（u0，v0）的值对应移动中心，则有

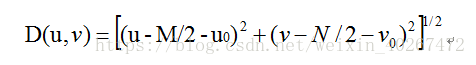
程序notchfilter.m为带阻陷波滤波器，分别为理想型、巴特沃斯、高斯带阻陷波滤波器，notchfilter_1.m为带阻陷波滤波器对。

2.算法思想及实验结果分析

(1)第一步，提取干扰模式的主频率成分。
通过观察傅立叶变换后的频谱图，也叫功率图，我们首先就可以看出，图像的能量分布，如果频谱图中暗的点数更多，那么实际图像是比较柔和的（因为各点与邻域差异都不大，梯度相对较小），反之，如果频谱图中亮的点数多，那么实际图像一定是尖锐的，边界分明且边界两边像素差异较大的。对频谱移频到原点以后，可以看出图像的频率分布是以原点为圆心，对称分布的。将频谱移频到圆心除了可以清晰地看出图像频率分布以外，还有一个好处，它可以分离出有周期性规律的干扰信号，比如正弦干扰，一副带有正弦干扰，移频到原点的频谱图上可以看出除了中心以外还存在以某一点为中心，对称分布的亮点集合，这个集合就是干扰噪音产生的，这时可以很直观的通过在该位置放置带阻滤波器消除干扰。
如图5为“水星6号”飞船拍摄的活性地形图像，图6为周期干扰的傅里叶频谱（由美国国家航空航天局提供），观察频谱，在每个尖峰处设一陷波带通滤波器H(u,v),即设置H(u,v)只可通过与干扰模式相关的成分，如图7所示，中间使用理想型高通滤波器和“+”型带阻滤波器，四角使用理想型带阻陷波滤波器。通过下式计算干扰噪声模式的傅里叶变换：

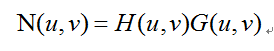
其中，G(u,v)为被污染图像的傅里叶变换。
然后通过傅里叶逆变换获得通过的噪声干扰，如图8所示。

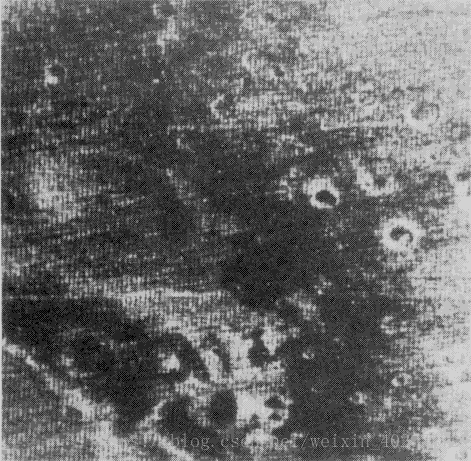
图5“水星6号”飞船拍摄的活性地形图像

图6 周期干扰的傅里叶频谱（由美国国家航空航天局提供）

图7 叠加在图6的陷波带通滤波器

图8 滤波后图像的傅里叶逆变换，在空间域显示噪声模式

（2）从受污染的图像g(x,y)减去模式得到f(x,y)是很简单的，但是这个滤波过程通常只会得到真实干扰模式的近似值。在噪声的估计中不存在的那些分量的影响可以被最小化，即通过从g(x,y)减去的加权来得到f(x,y)的估计值，如下所示：

其中，是的估计值，w(x,y)为加权函数。
此过程的目的就是选取加权函数，使得估计值在每一点(x,y)的指定领域的方差最小。考虑点(x,y)的尺寸为a*b的领域，假设w(x,y)在整个领域内保持不变（详细参考书p200），则w(x,y)解为：

利用上述两个式子来获得复原图像，详细可见程序optimum_notch.m。如果w(x,y)在某一领域内被假定为常量，则不必再像法1一样在图像中计算对应每对x,y值的函数值，而是在每个非重叠领域的一点（一般为中心点）计算w(x,y)值，然后处理该领域内包含的所有图像点，如法2，3，这样算法效率会搞一点。对于边界处理，可采用对称镜像填充法、零填充法等，这里采用了对称镜像填充法。

（实验分别使用理想滤波器、高斯滤波器和巴特沃斯滤波器进行滤波比较，以及a和b设置的相关实验，具体参看github）

实际天文图像应用成果

##原图（云南天文台拍摄）

傅里叶谱

滤波

噪声

本Markdown编辑器使用[StackEdit][6]修改而来，用它写博客，将会带来全新的体验哦：

结果图

代码下载https://download.csdn.net/download/weixin_40267472/11252576