一文读懂机器学习概率图模型（附示例&学习资源）

点击有惊喜

概率图模型是人工智能领域内一大主要研究方向。近日，数据科学家Prasoon

 Goyal在其博客上发表了一篇有关概率图模型的基础性介绍文章。文章从基础的概念开始谈起，并加入了基础的应用示例来帮助初学者理解概率图模型的实用价值。本文对该文章进行了编译介绍。

第一部分：基本术语和问题设定

机器学习领域内很多常见问题都涉及到对彼此相互独立的孤立数据点进行分类。比如：预测给定图像中是否包含汽车或狗，或预测图像中的手写字符是 0 到 9 中的哪一个。

事实证明，很多问题都不在上述范围内。比如说，给定一个句子“I like machine learning”，然后标注每个词的词性（名词、代词、动词、形容词等）。正如这个简单例子所表现出的那样：我们不能通过单独处理每个词来解决这个任务——“learning”根据上下文的情况既可以是名词，也可以是动词。这个任务对很多关于文本的更为复杂的任务非常重要，比如从一种语言到另一种语言的翻译、文本转语音等。

使用标准的分类模型来处理这些问题并没有什么显而易见的方法。概率图模型（PGM/probabilistic 

graphical model）是一种用于学习这些带有依赖（dependency）的模型的强大框架。这篇文章是 Statsbot 团队邀请数据科学家 Prasoon

 Goyal 为这一框架编写的一份教程。

在探讨如何将概率图模型用于机器学习问题之前，我们需要先理解 PGM 框架。概率图模型（或简称图模型）在形式上是由图结构组成的。图的每个节点（node）都关联了一个随机变量，而图的边（edge）则被用于编码这些随机变量之间的关系。

根据图是有向的还是无向的，我们可以将图的模式分为两大类——贝叶斯网络（ Bayesian network）和马尔可夫网络（Markov networks）。

1. 贝叶斯网络：有向图模型

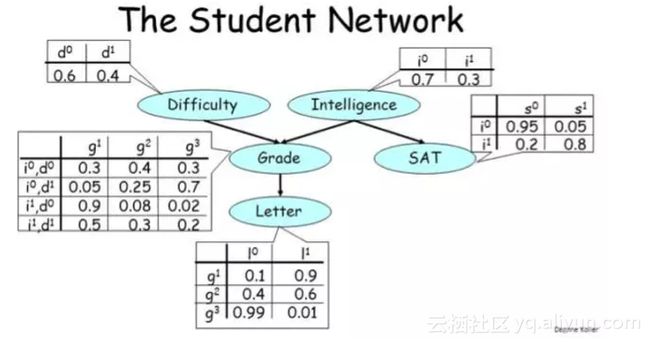
贝叶斯网络的一个典型案例是所谓的「学生网络（student network）」，它看起来像是这样：

这个图描述了某个学生注册某个大学课程的设定。该图中有 5 个随机变量：

• 课程的难度（Difficulty）：可取两个值，0 表示低难度，1 表示高难度；
  
• 学生的智力水平（Intelligence）：可取两个值，0 表示不聪明，1 表示聪明；
  
• 学生的评级（Grade）：可取三个值，1 表示差，2 表示中，3 表示优；
  
• 学生的 SAT 成绩（SAT）：可取两个值，0 表示低分，1 表示高分；
  
• 在完成该课程后学生从教授那里所得到的推荐信的质量（Letter）：可取两个值，0 表示推荐信不好，1 表示推荐信很好。
  

该图中的边编码了这些变量之间的依赖关系。

• 学生的 Grade 取决于课程的 Difficulty 和学生的 Intelligence；
  
• 而 Grade 又反过来决定了学生能否从教授那里得到一份好的 Letter；
  
• 另外，学生的 Intelligence 除了会影响他们的 Grade，还会影响他们的 SAT 分数。
  

注意其中箭头的方向表示了因果关系——Intelligence 会影响 SAT 分数，但 SAT 不会影响 Intelligence。

最后，让我们看看与每个节点关联的表格，它们的正式名称是条件概率分布（CPD/conditional probability distribution）。

条件概率分布

Difficulty 和 Intelligence 的 CPD 非常简单，因为这些变量并不依赖于其它任何变量。基本而言，这两个表格编码了这两个变量取值为 0 和 1 的概率。你可能已经注意到，每个表格中的值的总和都必须为 1。

接下来看看 SAT 的 CPD。其每一行都对应于其父节点（Intelligence）可以取的值，每一列对应于 SAT 可以取的值。每个单元格都有条件概率 p(SAT=s|Intelligence=i)，也就是说：给定 Intelligence 的值为 i，则其为 SAT 的值为 s 的概率。

比如，我们可以看到 p(SAT=s¹|Intelligence=i¹)

 是 0.8。也就是说，如果该学生的智力水平高，那么他的 SAT 分数也很高的概率是 0.8。而 p(SAT=s⁰|Intelligence=i¹) 则表示如果该学生的智力水平高，那么 SAT 分数很低的概率是 0.2。

注意，每一行中的值的总和为 1。这是当然而然的，因为当 Intelligence=i¹ 时，SAT 只能是 s⁰ 和 s¹ 中的一个，所以两个概率之和必定为 1。类似地，Letter 的 CPD 编码了条件概率 p(Letter=l|Grade=g)。因为 Grade 可以取 3 个值，所以这个表格有 3 行。

有了上面的知识，Grade 的 CPD 就很容易理解了。因为它有两个父节点，所以它的条件概率是这种形式：p(Grade=g|Difficulty=d,SAT=s)，即当 Difficulty 为 d 且 SAT 为 s 时 Grade 为 g 的概率。这个表格的每一行都对应于一对 Difficulty

 和 Intelligence 值。同样，每一行的值的总和为 1。

贝叶斯网络的一个基本要求是图必须是有向无环图（DAG/directed acyclic graph）。

2. 马尔可夫网络：无向图模型

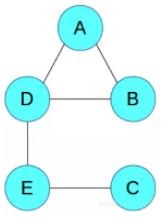
一个马尔可夫网络的简单例子：

为了简洁地说明，我们只探讨这个抽象的图，其中的节点 ABCDE 不像上面的例子有直接的真实案例对应。同样，这些边表示变量之间的相互作用。我们可以看到 A 和 B 彼此之间有直接的影响关系，而 A 和 C 之间则没有。注意马尔可夫网络不需要是无环的，这一点和贝叶斯网络不一样。

可能的用途

正如贝叶斯网络有 CPD 一样，马尔可夫网络也有用来整合节点之间的关系的表格。但是，这些表格和 CPD 之间有两个关键差异。

首先，这些值不需要总和为 1，也就是说这个表格并没有定义一个概率分布。它只是告诉我们值更高的配置有更高的可能性。其次，其中没有条件关系。它与所涉及到的所有变量的联合分布成正比，这与 CPD 中的条件分布不同。

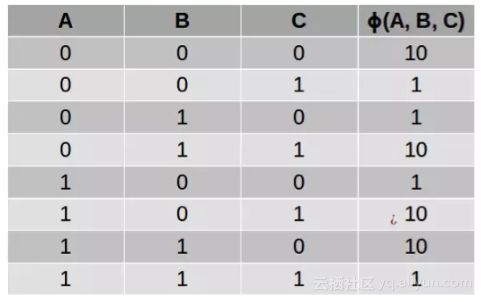
这样得到的表格被称为“因子（factor）”或“势函数（potential function）”，使用希腊字母φ 表示。比如，我们可以使用下面的势函数来描述变量 A、B 和 C 之间的关系，其中 C 是 A 和 B 的“软”异或（XOR），也就是说：如果 A 和 B 不一样，那么 C 很可能为 1；如果 A 和 B 一样，那么 C 很可能为 0：

一般而言，你要为图中的每个极大团（maximal clique）定义一个势函数。

图结构和表格就可以简洁地表示在这些随机变量上的联合概率分布。

现在你可能会有一个问题：为什么我们需要有向图，也需要无向图？原因是有些问题使用有向图表示会更加自然，比如上面提到的学生网络，有向图可以轻松描述变量之间的因果关系——学生的智力水平会影响 SAT 分数，但 SAT 分数不会影响智力水平（尽管它也许能反映学生的智力水平）。

而对于其它一些问题，比如图像，你可能需要将每个像素都表示成一个节点。我们知道相邻的像素互有影响，但像素之间并不存在因果关系；它们之间的相互作用是对称的。所以我们在这样的案例中使用无向图模型。

3. 问题设置

我们已经讨论了图、随机变量和表格，你可能会想所有这些有什么意义？我们到底想做什么？这里面存在机器学习吗？数据、训练、预测都在哪里？这一节将给你答案。

让我们再回到学生网络那个例子。假设我们已经有图结构了——我们可以根据我们对世界的知识进行创建（在机器学习中，这被称为领域知识（domain knowledge））。但我们没有 CPD 表，只有它们的规模。我们确实有一些数据——来自某所大学的十个不同课程，我们有这些课程的难度的测量方法。

另外，我们还有每个课程的每个学生的数据——他们的智力水平、他们的 SAT 分数、他们得到的评级以及他们是否从教授那里得到了好的推荐信。根据这些数据，我们可以估计 CPD 的参数。比如说，数据可能表明有高智力水平的学生往往有很好的 SAT 分数，然后我们可能会学习到：p(SAT=s¹|Intelligence=i¹) 很高。这是学习阶段。我们后面会介绍我们可以如何在贝叶斯网络和马尔可夫网络中执行这种参数估计。

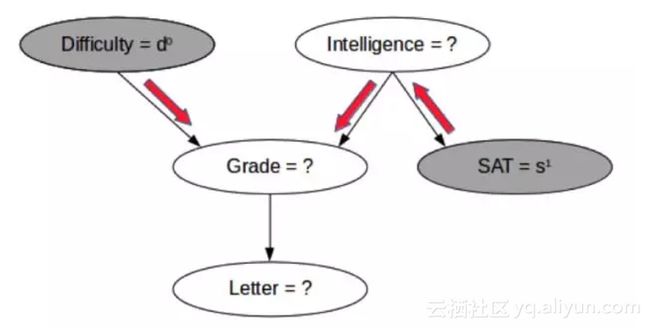
现在，对于一个新数据点，你可以看到其中一些变量，但不是全部变量。比如，在下面给出的图中，你可以知道一个课程的难度和学生的 SAT 分数，你想估计学生得到好的评级的概率。（现在你已经从学习阶段得到了表格中的值）

尽管我们没有可以给我们直接提供信息的 CPD，但我们可以看到有高 SAT 分数的学生说明该学生智力水平也很可能较高；由此，如果该课程的难度很低，那么该学生得到好评级的概率也会较高，如上图中的红色箭头所示。我们可能也想同时估计多个变量的概率，比如学生同时得到好评级和好推荐信的概率？

这种有已知值的变量被称为显变量（observed variable），而值未被观察到的变量被称为隐变量（hidden variable 或 latent 

variable）。一般来说，显变量用灰色节点表示，而隐变量则用白色节点表示，如上图所示。我们可能想要找到一些或全部显变量的值。

这些问题的解答类似于机器学习的其它领域——在图模型中，这个过程被称为"推理（inference）"。

尽管我们使用了贝叶斯网络来描述上述术语，但这也适用于马尔可夫网络。在我们深入用于学习和推理的算法之前，让我们先形式化我们刚刚看过的思想——给定某些节点的值，我们可以得到有关其它哪些节点的信息？

4. 条件独立

我们刚才探讨过的图结构实际上带有关于这些变量的重要信息。具体来说，它们定义了这些变量之间的一组条件独立（conditional independence），也就是这种形式的陈述——“如果观察到 A，那么 B 独立于 C。”让我们看一些例子。

在学生网络中，让我们假设你看到了一个有很高 SAT 分数的学生，你对她的评级怎么看呢？正如我们之前见过的那样，高 SAT 分数说明学生的智力水平很高，因此你可以预计评级为优。如果该学生的 SAT 分数很低呢？在这个案例中，你可以预计评级不会很好。

现在，让我们假设你不仅知道这个学生 SAT 分数较高，也知道她的智力水平也较高。如果 SAT 分数较高，那么你可以预测她的评级为优。但如果 SAT 分数较低呢？你仍然可以预计评级为优，因为这个学生的智能水平高，而且你可以假设她在 SAT 上表现得不够好。因此，知道这个 SAT 分数并不能让我们了解有关这个学生的智力水平的任何信息。要将其用条件独立的方式陈述，可以说——”如果已观察到 Intelligence，那么 SAT 和 

Grade 是独立的。“

我们是根据这些节点在图中的连接方式得到这个条件独立信息的。如果这些节点的连接方式不同，那么我们也会得到不同的条件独立信息。

让我们看看另一个例子。

假设你知道这个学生的智力水平高。你能对这门课程的难度有什么了解呢？一无所知，对吧？现在，如果我告诉你这个学生在这门课程上得到了一个差的评级，又会怎样呢？这说明这门课程很难，因为我们知道一个聪明的学生得了一个差。因此我们可以这样写我们的条件独立陈述——“如果未观察到 Grade，那么 Intelligence 和 Difficulty 是相互独立的。”

因为这些陈述都表达了在一定条件下两个节点之间的独立性，所以被称为条件独立。注意这两个例子有相反的语义——在第一个例子中，如果观察到相连的节点则独立性成立；第二个例子则是未观察到相连的节点则独立性成立。这种差异是由节点连接的方式（即箭头的方向）造成的。

为了行文简洁，我们不会在这里覆盖所有可能的情况，但这些情况都很简单，凭直觉就能看出来。

在马尔可夫网络中，我们可以使用类似的直觉，但因为其中没有有方向的边（箭头），所以其条件独立陈述相对简单——如果节点 A 和 B 之间没有路径能使得该路径上的所有节点都被观察到，那么 A 和 B 就是相互独立的。换种说法：如果在 A 和 B 之间至少有一条路径上的所有中间节点都未被观察到，那么 A 和 B 就不是相互独立的。

我们会在本博客的第二部分查看完成参数估计和推理的细节。现在让我们看看贝叶斯网络的应用，我们可以在其中用到我们刚学习到的条件独立思想。

点击有惊喜