吴恩达.深度学习系列-C4卷积神经网络-W1卷积神经网络基础

学习目标

• Understand the convolution operation
• Understand the pooling operation
• Remember the vocabulary used in convolutional neural network (padding, stride, filter, …)
• Build a convolutional neural network for image multi-class classification

1.计算机视觉

应用方式：
- Image Classification
- Object detection
- Neural Style Transfer
在大图片上进行深度学习。普通学习图片可以达到1000*1000*3（通道数）的级别。将是一个有3，000，000（3 million）特征数的输入。

2.边缘检测示例

垂直边缘检测，在课堂的实例中其实是使用了一个Prewitt的filter（filter过滤器，【图像处理】滤波器模板，神经网络的卷积核kernel指的都是一个意思）。参考本笔记12.2。

数学里，星号是卷积的标准符号，×是乘号。但是一般编程语言里星号 表示乘法。卷积操作是矩阵求内积。

Horizontal：⎡⎣⎢10−110−110−1⎤⎦⎥Vertical:⎡⎣⎢111000−1−1−1⎤⎦⎥ H o r i z o n t a l ： [ 1 1 1 0 0 0 − 1 − 1 − 1 ] V e r t i c a l : [ 1 0 − 1 1 0 − 1 1 0 − 1 ]

3.其他边缘检测

如上图上下所示。
颜色由深变浅，产生正边缘。颜色由浅入深，产生负边缘。
更据filter的不同数值填入，检测器会具备一些独特的边缘检测，除了水平、垂直检测，还有可能45度检测，75度检测，72度检测等等等等。

卷积神经网络的独特之处：将filter中的元素当作参数去学习，并通过反向传播让模型自己去学习该设置什么值。而这将生成更加善于捕捉你的数据的统计学特征的过滤器。并且很有可能超过CV专业人员精心设计的filter数值。简而言之，训练CNN在相当意义上是在训练每一个卷积层的滤波器。让这些滤波器组对特定的模式有高的激活，以达到CNN网络的分类/检测等目的。

在单层卷积后，通常能提取出横向、纵向、斜向的边缘这样的简单特征。经过多次卷积后，filter能通过学习提取出复杂的组合特征。例如眼睛、鼻子等等由多种线条组合而成的图形，这些高维特征是一系列低维特征的组合。在一些论文中有将这些卷积后的图片显示出来供研究人员观察，观察卷积网络学习到的是些什么图像。“反卷积”是不是这种应用的定义？

4.Padding

不padding的情况下：（n×n）的图片，用（f×f）的filter卷积，产生的输出大小（n-f+1）×(n-f+1)

不进行padding的缺点：

• 输入图片的边缘像素，因为不处于对称中心点，被卷积遍历运算引用的次数比图像中心区域的像素点少的多。即我们会丢失图像靠近边界的信息。
• 每一次卷积图片都会缩小，多次卷积图片将变得非常的小。

所以，有必要进行padding（补白）。比如输入图片是（6×6）padding成（8×8）的图片后，再进行kernel=（3×3）的卷积，输出将还是一个（6×6）的图像。

	Padding/Not	Cool
“Valid” convolution	no Padding	会忽略图像边缘的信息
“Same” convolution	Pad so that output size is the same as the input size.	单侧padding的像素个数p=(f-1)/2时 输出图片与输入图片同样大小

5.卷积步长 strided convolution

就是filter每次移动的步长。通常情况下，步长=1。如果设定步长=2，前后两次filter的起始位置相距2个像素（水平方向移动是相距2个像素，换行时也是下降两像素）。下图示例就是strided=2的情形。

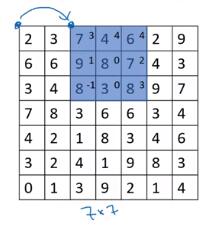
filter大小是（f×f），加上Strided(s)、padding(p是单侧补上的像素宽度)后，输入图片（n×n）与输出图片大小间的关系是：

输出图片:h=w=⌊n+2p−fs+1⌋ 输 出 图 片 : h = w = ⌊ n + 2 p − f s + 1 ⌋

,即向下取整 floor() f l o o r ( )

互相关（cross-correlation）与卷积

在数学教材书籍上，卷积操作需要对卷积核先做水平与垂直翻转，再求卷积。这会产生一种性质：（A卷积B）* 卷积C = A卷积 *（B卷积C) ，这一性质在数学上叫结合率（associativity），这一性质在信号处理领域很有用 但对深度神经网络而言，它并不重要 。从数学定义上，我们现在进行的“无翻转卷积核”操作最好称之为交叉相关。

但在机器学习的约定中， 我们通常忽略掉翻转的操作，并将这称之为卷积。

6.在三维图像（RGB）上进行卷积

在二维（W×H）图像上的卷积示意图：

Convolutions over Volume

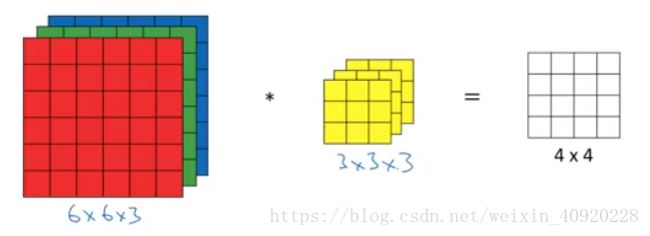
对于一个多通道图片，以RGB图片举例是3通道，要建立一个对等通道数的filter，即RGB图片要3个filter。这3个filter分别与原始图片的三个通道进行卷积操作。合计求和成一个值填入输出图像上。
所以虽然输入图像有3层，但输出图像是单层的。
如何在应用中应用多个过滤器

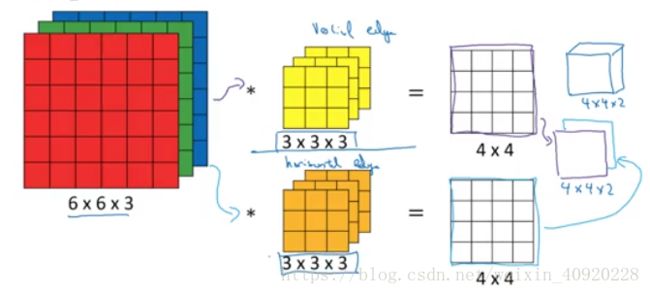
应用两个过滤器，那么输出就是两层。这两层也是下一层的输入。实际上你可以在同一层应用很多个filter来捕捉原始图片上各种各样的特征。
summary：
原始图片（n×n×nc）∗filter(f×f×nc)→(n−f+1)×(n−f+1)×n′c 原 始 图 片 （ n × n × n c ） ∗ f i l t e r ( f × f × n c ) → ( n − f + 1 ) × ( n − f + 1 ) × n c ′
n′c n c ′ ,是下一层的 nc n c ，等于应用过滤器的数量

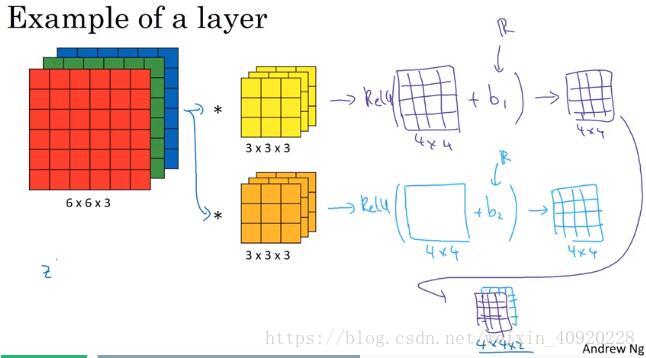
7.单层式卷积网络one Layer of a Convolution Network

如上图所示，一层完整卷积层，包括

1. 使用n个filter进行卷积，
2. 每个filter输出的卷积结果加上各自的偏置量，得出Z（一个卷积核共享一个b）
3. 对这个Z进行激活操作，比如relu。
4. 最终的输出结果有n层（depth=n）

卷积网络的参数数量计算
If you have 10 filters that are 3×3×3 in one layer of a neural network,how many parameters does that layer have?
NumberParameters=（单个kernel的参数量+1个偏置量）×filter总数=[(3×3×3)+1]×10=280 N u m b e r P a r a m e t e r s = （ 单 个 k e r n e l 的 参 数 量 + 1 个 偏 置 量 ） × f i l t e r 总 数 = [ ( 3 × 3 × 3 ) + 1 ] × 10 = 280

优点：无论输入层多大（输入的图片多大），参数量恒定。相比普通神经网络输入有多少个特征就至少有 n0∗n1 n 0 ∗ n 1 个参数，尤其针对比如2000*2000这样大型的图片输入，这的确会大大减少了参数数量，这便是卷积层的“权值共享”特性，能使得卷积神经网络更不容易过拟合。

标注说明：
f[l] f [ l ] ,表示第l层filter的size
p[l] p [ l ] ,表示第l层padding的单侧像素宽度
s[l] s [ l ] ,表示第l层的stride
n[l]c=f[l] n c [ l ] = f [ l ] ,输出图像的深度
输入图像的H!=W时：

n[l]H=⌊n[l−1]H+2p[l]−f[l]s[l]+1⌋，n[l]W=⌊n[l−1]W+2p[l]−f[l]s[l]+1⌋ n H [ l ] = ⌊ n H [ l − 1 ] + 2 p [ l ] − f [ l ] s [ l ] + 1 ⌋ ， n W [ l ] = ⌊ n W [ l − 1 ] + 2 p [ l ] − f [ l ] s [ l ] + 1 ⌋

8.简单型卷积网络示例

1）登记好输入层 a[0] a [ 0 ] 的shape，记录将要进行的卷积的filter size，stride，padding num，filter num。
2）计算输出的shape, a[1] a [ 1 ]
3）登记下一个卷积的filter size，stride，padding num，filter num
4）计算输出的shape, a[2] a [ 2 ]
5) ……
6) 比如最后的卷积输出shape是，(7×7×40)有40个特征层，将(7×7×40)扁平化为一个1960向量，连接softmax进行分类判断。
一个典型的卷积神经网络的层次结构如下图：

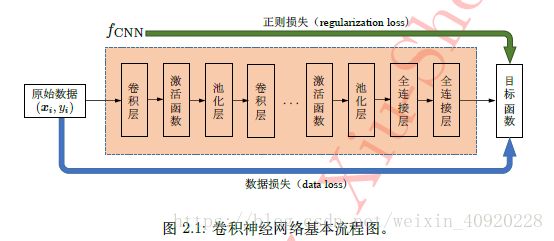
9.池化层 Pooling Layers

相对于卷积层对filter进行求内积，池化层是对filter size内的输入数据，求最大值（max pooling）或求平均值（average pooling）。无论是最大值还是平均值，相当于对输入数据指定区域进行一次“关键特征的提取”，经过pooling后，图片的大小会缩小，所以也被称为降采样（down-sampling）操作。另一方面，汇合也看成是一个用p范数（p-norm）作为非线性映射的“卷积”操作，特别的，当p 趋近正无穷时就是最常见的最大值汇合。
汇合层具备如下三种功效：

1. 特征不变性（feature invariant）。汇合操作使模型更关注是否存在某些特征而不是特征具体的位置。可看作是一种很强的先验，使特征学习包含某种程度自由度，能容忍一些特征微小的位移。
2. 特征降维。由于汇合操作的降采样作用，汇合结果中的一个元素对应于原输入数据的一个子区域（sub-region），因此汇合相当于在空间范围内做了维度约减（spatially dimension reduction），从而使模型可以抽取更广范围的特征。同时减小了下一层输入大小，进而减小计算量和参数个数。

3. 在一定程度防止过拟合（overfitting），更方便优化。【注：减少参数，被认为是能减少过拟合】

   卷积与池化操作的对比如下：

-	卷积操作	池化操作
计算	对filter求内积	对filter取max/average
参数	filter（卷积核）的参数学习	无
需指定filter size	有	有
需指定stride	有	有
padding	有	无
是否需学习参数	是	否（只需指定超参数，没有要学习的参数）
输出的层数（depth，channel）	等于filter的个数	等于输入的层数，不改变输入的depth

10.卷积神经网络示例（CNN Example）

池化层是否被计算为1层？课程认为，没有需要学习的参数的层不被单独计算为一层，所以，本课程将遵循，将卷积+池化共同计为一层的方式。
各层的特征个数，与参数数量：

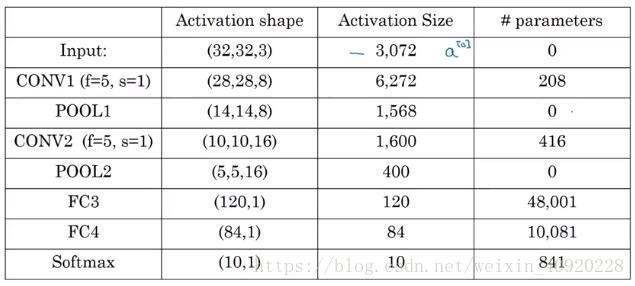
可以看到参数的大部分在全连接层上。

网络中每一层的特征个数，应该要逐渐下降，减少的太快通常认为不利于网络的性能

下图是AlexNet网络结构。AlexNet在当时被认为是划时代的网络模型。但是神经网络发展太快，现在比它先进的多的网络模型不断涌现。但是AlexNet当时的设计思路，和许多特点还是能给予借鉴。

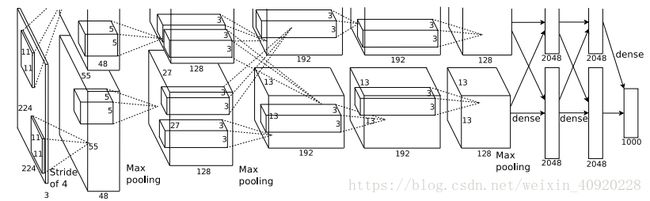
11.为何要用卷积？

加入卷积层后的优点：
1. 参数共享（或称权值共享，weight sharing，Parameter sharing）: 参考第7.小节中关于优点“权值共享”的描述。
2. 稀疏式连接（Sparsity of connections）:卷积输出的单个值，只是跟少数输入数据相关。而不像全连接神经网络，每个输出值都与所有输入单元相关。这就是稀疏式连接
3. 平移不变性（translation invariant）：卷积帮助网络在输入图片上下左右移动主要识别物体后，如“猫”，能够获得相同的识别结果。

12.practic

What do you think applying this filter to a grayscale image will do?

⎡⎣⎢⎢⎢01101331−1−3−3−10−1−10⎤⎦⎥⎥⎥ [ 0 1 − 1 0 1 3 − 3 − 1 1 3 − 3 − 1 0 1 − 1 0 ]

答：这个卷积核是进行垂直边缘检测

You have an input volume that is 32x32x16, and apply max pooling with a stride of 2 and a filter size of 2. What is the output volume?
答：使用pooling层输出大小计算公式 ⌊n−fs+1⌋ ⌊ n − f s + 1 ⌋

Because pooling layers do not have parameters, they do not affect the backpropagation (derivatives) calculation.
答：不对。方向传播中，pooling层要按max（只传递给最大值），或 average（传递给filter覆盖的所有值）方式规则将梯度反向传给前一层。因此不能说它不影响计算。

13.番外，卷积核的数学意义

参考：《解析卷积神经网络》-魏秀参
深度学习的一个重要思想即“端到端”的学习方式（end-to-end manner），属
表示学习（representation learning ）的一种。
在深度学习时代之前，样本表示基本都使用人工特征（hand-crafted），但“巧妇难为无米之炊”，实际上人工特征的优劣往往很大程度决定了最终的任务精度。这样便催生了一种特殊的机器学习分支——特征工程（feature engineering）。[“A Performance Evaluation of Local Descriptors”系统性的解释不同局部特征描述子的作用，2013年深度学习巨头Yoshua Bengio就认为，深度学习将替代特征工程]而在深度学习普及之后，人工特征已逐渐被表示学习根据任务自动需求“学到”的特征表示所取代。

13.1.拉普拉斯算子(卷积核)

参考：《数字图像处理》-冈萨雷斯
卷积核在数字图像处理领域叫“算子”，是对图像不同轴向求微分近似值，从而达到提取图像边缘信息的一种方法。
原图与不同算子卷积后的效果图。

整体边缘滤波器 拉普拉斯算子	横向边缘滤波器 sobel横向算子	纵向边缘滤波器 sobel纵向算子
⎡⎣⎢0−40−416−40−40⎤⎦⎥ [ 0 − 4 0 − 4 16 − 4 0 − 4 0 ]	⎡⎣⎢10−120−210−1⎤⎦⎥ [ 1 2 1 0 0 0 − 1 − 2 − 1 ]	⎡⎣⎢121000−1−2−1⎤⎦⎥ [ 1 0 − 1 2 0 − 2 1 0 − 1 ]

对于一维函数f(x)，其一阶微分的基本定义是差值：

∂f∂x=f(x+1)−f(x) ∂ f ∂ x = f ( x + 1 ) − f ( x )

二阶微分是如下的差分：

∂2f∂2x=(f(x+1)−f(x))−(f(x)−f(x−1)) ∂ 2 f ∂ 2 x = ( f ( x + 1 ) − f ( x ) ) − ( f ( x ) − f ( x − 1 ) )

=f(x+1)+f(x−1)−2f(x) = f ( x + 1 ) + f ( x − 1 ) − 2 f ( x )

而对于二维图像函数 f(x,y) f ( x , y ) ,就是沿着两个空间轴分别处理偏微分。
对于灰度过度的斜坡，其一阶微分不是零，二阶微分是零。这样导致图像的一阶微分会产生较粗的边缘，因为沿着斜坡的微分非零。二阶微分可以通过卷积来获得，这样在操作上也比一阶微分计算简单。所以在寻找图像边缘上使用二阶微分。

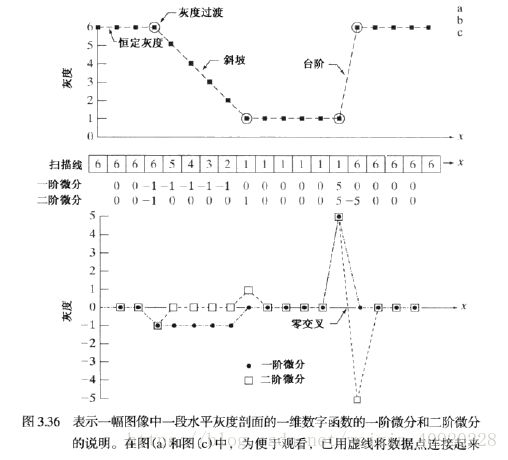
而在图片边缘提取的操作，基本上是由定义一个二阶微分的离散公式，然后构建一个基于该公式的滤波器模板组成。拉普拉斯算子是个各向同性微分算子。一个二维图象函数 f(x,y) f ( x , y ) 的拉普拉斯算子定义为：

▽2f=∂2f∂2x+∂2f∂2y ▽ 2 f = ∂ 2 f ∂ 2 x + ∂ 2 f ∂ 2 y

x方向：∂2f∂2x=f(x+1,y)+f(x−1,y)−2f(x,y) x 方 向 ： ∂ 2 f ∂ 2 x = f ( x + 1 , y ) + f ( x − 1 , y ) − 2 f ( x , y )

y方向：∂2f∂2y=f(x,y+1)+f(x,y−1)−2f(x,y) y 方 向 ： ∂ 2 f ∂ 2 y = f ( x , y + 1 ) + f ( x , y − 1 ) − 2 f ( x , y )

组合以上可以得到离散拉普拉斯算子：

▽2f(x,y)=$f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y) ▽ 2 f ( x , y ) = $ f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 4 f ( x , y )

楼上公式是x，y两个方向求二阶微分，还可以增加两个对角线上求二阶微分。增加两对角线后，总共应该减去 −8f(x,y) − 8 f ( x , y )

图a：标准负中心，两轴拉普拉斯滤波器模板
图b：标准负中心，两轴加对角拉普拉斯滤波器模板
图c：正中心，两轴拉普拉斯滤波器模板
图d：正中心，两轴加对角拉普拉斯滤波器模板

13.2从Robert,Prewitt算子到sobel算子

Sobel算子主要用作边缘检测，是检测图像灰度变化一阶导数的应用。在图像f的(x,y)位置处寻找边缘的强度和方向，选择的工具是梯度，并用向量来定义梯度 ▽f ▽ f

▽f(x,y)=[gxgy]=⎡⎣∂f∂x∂f∂y⎤⎦ ▽ f ( x , y ) = [ g x g y ] = [ ∂ f ∂ x ∂ f ∂ y ]

向量 ▽f ▽ f 的大小（长度）计算公式为：

G=g2x+g2y−−−−−−√ G = g x 2 + g y 2

这也是检测结果输出图上，该点的灰度值。另外还能得到梯度向量的法向量（正交）。

α(x,y)=actan[gygx] α ( x , y ) = a c t a n [ g y g x ]

要计算每个像素点位置的偏导数： gx=∂f(x,y)∂x=f(x+1,y)−f(x,y) g x = ∂ f ( x , y ) ∂ x = f ( x + 1 , y ) − f ( x , y ) ,
gy=∂f(x,y)∂y=f(x,y+1)−f(x,y) g y = ∂ f ( x , y ) ∂ y = f ( x , y + 1 ) − f ( x , y ) 。要计算这两个公式，可以使用一维模板对 f(x,y) f ( x , y ) 的滤波来实现。模板如下图：

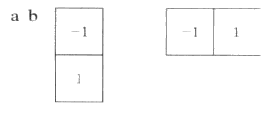
这样的一维模板及它的改进型Roberts交叉梯度算子2*2模板（检测对角线方向边缘），没有中心点对称。而有中心点对称最小得是3*3模板。那么用3*3的模板来近似偏导数的最简单的数字近似如下公式：(z 1~9是九宫格的顺序位置)
gx=∂f(x,y)∂x=(z7+z8+z9)−(z1+z2+z3) g x = ∂ f ( x , y ) ∂ x = ( z 7 + z 8 + z 9 ) − ( z 1 + z 2 + z 3 )
gy=∂f(x,y)∂y=(z3+z6+z9)−(z1+z4+z7) g y = ∂ f ( x , y ) ∂ y = ( z 3 + z 6 + z 9 ) − ( z 1 + z 4 + z 7 ) 其对应的滤波器模板是Prewitt。

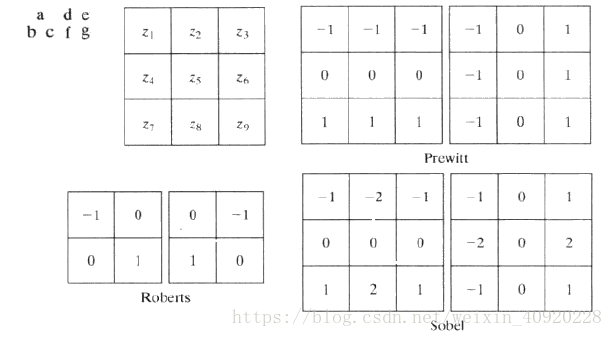
因为考虑了对称因素，Prewitt算子要比Robert算子得到的近似更准确。而在中心位置增加权重就得到了Sobel算子。
Sobel算子根据像素点上下、左右邻点灰度加权差，在边缘处达到极值这一现象检测边缘。对噪声具有平滑作用，提供较为精确的边缘方向信息，但边缘定位精度不够高（它会在灰度的分界线左右两侧各产生一条边缘，即sobel画出的边缘比较粗）。当对精度要求不是很高时，是一种较为常用的边缘检测方法。
实际应用中因为求平方再开根的运算开销大，会使用如下绝对值方式来近似梯度。

G=g2x+g2y−−−−−−√≈|gx|+|gy| G = g x 2 + g y 2 ≈ | g x | + | g y |

【详细的还是看书吧，书上已经说的够明白了，不知道要怎样才能简化摘录出来。】

14.编程题

卷积过程相关代码

Z1 = tf.nn.conv2d(X,W1, strides = [1,1,1,1], padding = ‘SAME’)

**Notation：**CONV2D: stride of 1, padding ‘SAME’
tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, name=None)

name参数用以指定该操作的name

第一个参数，input：指需要做卷积的输入图像，它要求是一个Tensor，具有[batch, in_height, in_width, in_channels]这样的shape，具体含义是[训练时一个batch的图片数量, 图片高度, 图片宽度, 图像通道数]，注意这是一个4维的Tensor，要求类型为float32和float64其中之一。图像通道数可以是输入图像RGB的3通道，也可以是经过n个filter卷积后的n通道。

第二个参数，filter：相当于CNN中的卷积核，它要求是一个Tensor，具有[filter_height, filter_width, in_channels, out_channels]这样的shape，具体含义是[卷积核的高度，卷积核的宽度，图像通道数，卷积核个数]，要求类型与参数input相同，有一个地方需要注意，第三维in_channels，就是参数input的第四维

第三个参数，strides：卷积时在图像每一维的步长，这是一个一维的向量，长度4。通常input的第一维是样本数m，第四维是channel，所以1，4维通常stride=1。strides=[1,s,s,1],s是在图像中卷积的步长。

第四个参数，padding：string类型的量，只能是”SAME”,”VALID”其中之一。”SAME”=padding，并且输出图像h*w等于输入图像h*w，”VALID”=no padding

第五个参数，use_cudnn_on_gpu:bool类型，是否使用cudnn加速，默认为true。

A1 = tf.nn.relu(Z1)

tf.nn.relu(features, name = None)
这个函数的作用是计算激活函数 relu，即 max(features, 0)。即将矩阵中每行的非最大值置0。

P1 = tf.nn.max_pool(A1, ksize = [1,8,8,1], strides = [1,8,8,1], padding = ‘SAME’)

**Notation:**MAXPOOL: window 8x8, sride 8, padding ‘SAME’
tf.nn.max_pool(value, ksize, strides, padding, name=None)
参数是四个，和卷积很类似：
第一个参数value：需要池化的输入,对应conv2d的input，一般池化层接在卷积层后面，所以输入通常是feature map，依然是[batch, height, width, channels]这样的shape

第二个参数ksize：池化窗口的大小，取一个四维向量，一般是[1, height, width, 1]，因为我们不想在batch和channels上做池化，所以这两个维度设为了1

第三个参数strides：和卷积类似，窗口在每一个维度上滑动的步长，一般也是[1, stride,stride, 1]

第四个参数padding：和卷积类似，可以取’VALID’ 或者’SAME’

返回一个Tensor，类型不变，shape仍然是[batch, height, width, channels]这种形式

P2 = tf.contrib.layers.flatten(P2)

tf.contrib.layers.flatten(P)这个函数就是把P保留第一个维度，把第一个维度包含的每一子张量展开成一个行向量，返回张量是一个二维的， shape=（batch_size，….）,一般用于卷积神经网络全链接层前的预处理

Z3 = tf.contrib.layers.fully_connected(P2, 6,activation_fn=None)

tf.contrib.layers.fully_connected(
inputs, num_outputs, activation_fn=tf.nn.relu, normalizer_fn=None, normalizer_params=None,
weights_initializer=initializers.xavier_initializer(), weights_regularizer=None,
biases_initializer=tf.zeros_initializer(), biases_regularizer=None,
reuse=None, variables_collections=None, outputs_collections=None,
trainable=True, scope=None)常用参数就3个
tf.contrib.layers.fully_connection(F，num_output,activation_fn)这个函数就是全链接成层
全连接实际上是完成一个 g(W*X+b）,权重乘输入加偏置量再激活的过程。对应的w初始化由tensorflow自动完成，无需指定。
F是输入，num_output是下一层单元的个数，activation_fn是激活函数

• inputs: A tensor of at least rank 2 and static value for the last dimension; i.e. [batch_size, depth], [None, None, None, channels]
• num_outputs: Integer or long, the number of output units in the layer.
• activation_fn: Activation function. The default value is a ReLU function. Explicitly set it to None to skip it and maintain a linear activation.

cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = Z3, labels = Y))

tf.nn.softmax_cross_entropy_with_logits(logits, labels, name=None)
除去name参数用以指定该操作的name，与方法有关的一共两个参数：
第一个参数，logits：就是神经网络最后一层的输出，如果有batch的话，它的大小就是[batchsize，num_classes]，单样本的话，大小就是num_classes
第二个参数，labels：实际的标签，大小同上
tf交叉熵函数有4个：

• tf.nn.sigmoid_cross_entropy_with_logits(_sentinel=None, labels=None, logits=None, name=None)
• tf.nn.softmax_cross_entropy_with_logits(_sentinel=None, labels=None, logits=None, dim=-1, name=None)
• tf.nn.sparse_softmax_cross_entropy_with_logits(_sentinel=None, labels=None, logits=None, name=None)
• tf.nn.weighted_cross_entropy_with_logits(labels, logits, pos_weight, name=None)

tf.reduce_mean(input_tensor, reduction_indices=None, keep_dims=False, name=None)
参数1–input_tensor:待求值的tensor。
参数2–reduction_indices:在哪一维上求解。
参数（3）（4）可忽略

optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)

此函数是Adam优化算法：是一个寻找全局最优点的优化算法，引入了二次方梯度校正。
相比于基础SGD算法，1.不容易陷于局部优点。2.速度更快