尤肖虎等:基于AI的5G技术:4大研究方向、4个典型范例
尤肖虎等:基于AI的5G技术:4大研究方向、4个典型范例
本文作者
尤肖虎:东南大学教授,移动通信国家重点实验室主任
张 川:东南大学信息科学与工程学院副教授
谈晓思:移动通信国家重点实验室(东南大学信息科学与工程学院)博士后
金 石:东南大学教授,博导,国家自然科学基金杰出青年科学基金获得者
邬贺铨:中国工程院院士
来源:公众号5G http://www.sohu.com/a/240309808_358040
时间:2018-07-10
1. 引言
5G是面向2020年之后发展需求的新一代移动通信系统,其主要目标可概括为“增强带宽、万物互联”。5G应用被划分为三个典型场景:eMBB、mMTC以及URLLC,并规定了多维度的关键技术指标需求,包括:峰值速率、频谱效率、时间延迟、网络可靠性、连接密度、以及用户体验速率等。大规模天线阵列、密集网络、新型波形复用与信道编译码(如极化码)、以及毫米波接入将成为5G无线网络的核心关键技术[1]。5G另一项富有前景的关键技术是网络虚拟化与切片技术,其基本思想是将5G网络构建在云计算平台上,通过计算资源的隔离、动态调配与迁移,实现网络资源的灵活调配,以适应未来5G极为丰富的应用场景。
5G技术标准正处于不断完善与成熟的过程中[2,3]。3GPP与2017年12月公布了第一个5G技术标准,支持NSA与eMBB功能[4]。2018年6月14日,3GPP批准了5G SA技术标准,5G自此进入了产业全面冲刺的新阶段[5]。在4G技术基础上,5G NR:1)对已有的MIMO技术进行了增强,引入了大规模天线阵列技术;2)对OFDM时隙结构和时频资源块RB划分方案进行了补充,提出了更为灵活的空中接口技术;3)预计下一个5G标准版本将引入NOMA技术,以支持广域覆盖的中低速率物联网应用;4)沿用了前期的分布式无线网络架构[6],将无线网络功能单元划分为分布式单元DU和中心单元CU,并引入了基于云计算的网络虚拟化与切片技术。5G技术应用范围的扩展使得其系统设计和优化更为复杂。传统移动通信系统的优化目标主要体现在,对系统传输速率和移动性能力的支持。5G NR将其应用特性的支持能力进一步扩展至:时间延迟、网络可靠性、连接密度、及用户体验速率等多个关键性指标方面。5G NR系统设计需要在这些KPI之间进行这种与优化[7]。而且灵活空中接口、网络虚拟化与切片技术的引入,极大地增加了系统设计的复杂性,并为5G网络运维和优化带来了极大的挑战。可喜的是,AI技术为5G系统的设计与优化提供了一种超越传统理念与性能的可能性,以成为业界重点关注的研究方向。
AI技术诞生于20世纪中叶,几经沉浮,近年来借助于现代计算和数据存储技术的迅猛发展而再次复兴。AI技术涵盖遗传算法[8]和人工神经网络[9、11]两大类,其本身是一种普适性的机器学习技术。凡是给定场景涉及了数据的统计、推断、拟合、优化、及聚类,AI均能找到其典型应用。AI学习算法又可以粗略地分为监督学习和非监督学习两类。前者的典型例子是:通过一组先验的数据对(data pairs)对多层人工神经网络(见图1)节点间的加权系数进行离线训练。
图1 监督学习实例:多层人工神经网络学习
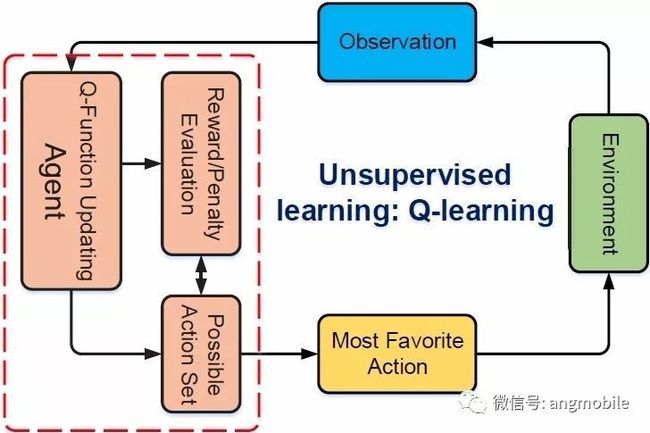
当训练收敛后,该分层人工神经网络可以实现对新的数据的辨识与推断。后者的典型例子是:可在线处理的增强学习方法(见图2)。它基于智能实体(Agent)与环境(environment)之间的动态交互。当智能实体感知到环境信息后,依据自己采取动作(Action)所可能带来的奖励(Reward)或惩罚(Penalty),确定下一步动作,并进一步观察环境的反应,循环往复,直至收敛至某一稳态目标。
图2 非监督学习实例:Q学习算法
两种常见的学习方法如下:
反向传播(BP)学习算法:BP学习算法是分层人工神经网络中最为典型的训练算法[9],是最速下降优化算法的一种具体形式。其目标是通过迭代,调整节点间的加权系数,使得分层人工神经网络的输出逐步接近已知的输出。有关BP算法的动态参数优化及加速实现形式,可参见作者早期的有关论文[10、11]。有关分层人工神经网络拓扑结构的选择,以及如何避免陷入局部最优可参见作者早期论文[12]。而今,BP学习算法被广泛用于训练深度神经网络(DNN),并取得了良好的效果。拥有两层或更多隐藏层的神经网络均可被称为DNN。卷积神经网络(CNN)是一类常见的前馈DNN,其隐藏层包含:卷积层、池化层、全连接层、及归一化层。CNN也可使用发现传播算法进行训练,并能在图像和语音识别等方面给出比其他DNN更好的结果。
Q学习算法:Q学习算法又称为Bellman算法[13],是增强学习最为经典的算法。其基本思路是:选择某一函数(Q函数),作为衡量一个智能实体执行某种动作的代价函数;该智能实体根据所处的环境,对所有可能的动作进行Q函数评估,并从中选择出奖励成为最大的动作,并加以行动。Bellman给出了Q函数最常见的迭代更新形式,从而使该智能实体的动作、环境变化和Q函数的调整能以在线的方式实现。Q算法的迭代收敛性证明可参见论文[14]。
2. AI应用于5G系统的发展方向
作为普适性的机器学习技术,AI可以广泛应用于5G系统设计和优化的各个缓解,大体上设计三类技术问题:组合优化问题、检测问题、估计问题。
首先,5G NR的资源分配问题是一个典型的组合优化问题。它需要从资源池中穷举出一组最优的资源配置方式,并据此将资源分配给网络覆盖范围内的多个用户,最大化资源利用率。再如,5G通信最优接收机的设计就是一个典型的检测问题,其目标是对接收信号进行辨识,确定对应的发射信号,并使检测错误概率最低。第三,5G通信的信道参数的准确估计是实现系统相干接收的必要条件。它需要根据5G系统所发送的导频信号估计出无线信号传播从发射端到接收端所经历的信道畸变。
AI技术在5G系统中的应用已经有大量的文献[15-23]可供参考,但并非所有的研究均有潜在的发展生命力。首先,移动通信系统本身经过长期的发展,已经具有了较为完备的经典设计和处理方法;大量实践已经证明,这些经典方法在工程上极为有效,且易于实现。其次,移动通信系统通常存在性能界限(如香农容量极限),现有的方法经过精心设计已经可以充分逼近上述性能界。例如,文献[24]中给出了逼近MIMO容量界的一种设计方法,其只需对功率最优注水分配问题进行简单的迭代,便可使MIMO的系能充分逼近香浓容量界。这意味着,即使采用先进的AI学习技术,也无法超越这些经典算法。第三,AI学习本身也有明显的局限性,无论是BP算法还是Q算法均存在训练的收敛时间问题。能否满足移动通信系统实时处理的需求,需要进行较为充分的评估。最后,与经典算法相比,AI学习算法的计算复杂度通常较高,如果不能带来性能上明显的提升,其本身显然不具备足够的竞争力。
这里并非否定AI技术在5G系统设计与优化中的潜在价值。相反,5G系统中存在大量传统方法难以建模、求解、或高效实现的问题,为AI技术在5G中的有效应用提供了可能。因此,有必要对AI技术在5G系统设计与优化的典型问题进行梳理,从而确定其5G系统中更有潜在应用价值的研究方向。
为此,本文将AI在5G中的应用问题划分为一下四类问题:无法建模问题、难以求解问题、统一模式高效实现问题、以及最优检测与估计问题。我们看到:对于前两类问题,由于缺乏有效的传统解决方案,AI技术通常根具应用潜力。而对于后两类问题,AI技术相对于传统的解决方案是否在性能或实现上具备更强的竞争力,则视其具体解决方案而定。四类问题具体分析如下。
无法建模问题:移动通信系统的网络优化涵盖一类难以统一建模的技术问题,如:覆盖问题、干扰问题、邻区选择、及越区切换问题等,其运维通常更多地依赖于工程人员的实践经验。相比之下,5G系统涉及的应用场景更为综合、KPI种类更多,特别是5G NR中基于大规模天线阵列的密集波束应用[25],需要引入更高维度的优化参数,对网络运维带来了更为艰巨的挑战。5G NR另一个难以建模的问题是KPI优化。如前所述,5G NR的KPI涉及峰值速率、频谱效率、时间延迟、网络可靠性、连接密度、以及用户体验速率等多个维度,这些指标往往是相互依赖或者相互矛盾的[7],因而难以建立全局性的优化模型。
难以求解问题:5G NR设计一系列资源分配问题[25、26],包括:小区时频资源块分配、正交导频资源分配、波束分配、大规模MIMO多用户聚类、无线网络虚拟化资源池调配等。这些问题的模型优化目标是使得真个无线网络的吞吐率最大化,并满足一定程度的用户服务比例公平性。其最优解求解问题通常属于NP-hard类型的组合优化,对应的计算复杂度随系统规模的增加而指数增长。传统的解决方法一般将此类问题进行静态分割,从而以较低的计算量获取次优的解决方案。AI技术则为此类问题的解决提供了可能的技术途径。
统一模式高效实现问题:5G NR涉及一些基本功能模块的级联组合。以5G NR的物理层为例,涉及:大规模MIMO多用户空时处理、NOMA信号检测、及LDPC码和Polar码信道编译码等功能模块。上述每个功能模块算法各不相同,但理论上均可以单独采用AI学习技术逐一加以解决[15-23]。这启发我们,可用统一的、基于AI技术的软硬件方案解决5G NR物理层所有的关键功能模块[27],从而简化系统的设计流程、加速工程实现的进程、提高物理层实现的可配置性,并最终降低系统实现成本、提高实现效率。
最优检测与估计问题:将AI应用于5G系统的直观想法是,用人工神经网络来取代传统发射机和接收机的基本功能模块。如前所述,基于人工神经网络训练的方法,其无线传输性能最多也只能接近香农容量界;但相对于经典的优化设计方法,其计算量可能更为庞大,且训练所需的收敛时间也会限制其实际有应用。另一个更值得探讨的研究方向是,使用AI技术进行跨层联合优化[28],包括物理层与MAC层的联合优化[29]、信源与信道的联合优化[30]、算法设计与硬件实现的联合优化[31]等,这些均是传统方法所难以解决的。
3 AI应用于5G系统的典型范例
本节将具体介绍AI应用于5G系统的四个典型范例:网络自组织与自由化、时频资源最优分配、5G通用加速器、以及5G物理层端到端优化。
3.1 网络自组织与自由化
SON已被3GPP列为LTE网络优化关键技术。相比于传统无线通信,5G应用场景更为复杂,网络优化与管理更为艰难,因此对SON的技术需求将更为强烈。SON包括了网络自配置、自由化、及自愈合三项功能,旨在淡化传统人工干预,实现网络规划、网络配置及网络优化的高度自动化,以节省运营成本,降低认为故障。文献[32-34]对AI技术在SON中的应用进行了总结,涉及基站自主参数配置、动态规划、迁移学习、网络故障的自动检测与定位、及网络参数的自动优化等,所采用的AI方法包括人工神经网络学习、蚁群优化、以及遗传算法等。
下面以文献[35]提出的自动故障分析为例,介绍AI技术在SON中的具体应用。为了实现LTE网络自动故障诊断,AI技术需要克服两大问题:1)现有大量数据的KPI种类多,又缺乏已知的故障标签,难以进行简单的归类诊断;2)鉴于人工诊断的成本较高和能力有限,需要尽量减少人工参与。因此,研究者[35]结合监督和无监督两种学习方法,提出了基于AI的故障诊断系统。诊断分为以下几步:
1、利用无监督的自组织映射(SOM)算法实现对无标签高维度数据的初步分类。多种类的KPI指标带来了高纬度的历史数据。SOM作为人工神经网络,通过训练能将任意维度的输入数据在输出层映射成二维神经元网络。神经元的拓扑结构即代表了原数据的分布情况:越相近的神经元,其映射的原数据越接近。这样就实现了高维度数据的低维度表示和初步聚类。
2、完成SOM训练后,再对SOM建立的神经元进行一次无监督的聚类。因为神经元之间的欧氏距离即表示其映射数据之间的差异,所以基于欧氏距离的沃德(Ward)聚类算法即可实现对神经元的聚类。
3、经过以上两个步骤,数据已经被分为几个大类。此时,再引入专家对分好类的数据进行故障分析,有监督地贴上故障标签。
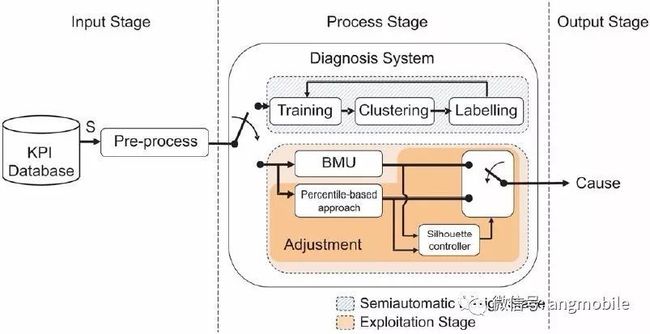
以上三个步骤完成了故障诊断系统的设计,建立了一套自动的诊断流程,如图3所示。此后产生的心数据在输入该系统之后,将先有SOM定位到最接近的神经元,再由该神经元的类别标签判断其是否故障以及原因。在诊断一定数量的新数据之后,以上三个步骤可以再次被执行用以验证和更新系统。文献[35]的仿真结果表明,即便在主要使用无监督学习进行构建、并且人工参与量极低的情况下,上述自动故障诊断系统仍能达到非常高的诊断准确率。
图3 自动故障诊断系统流程
3.2 时频资源最优分配
相比于4G LTE-A,5G NR将面临更为复杂的OFDM时频资源块RB分配问题,以适应5G三种典型的应用场景。图4给出了一个典型的多校区、多用户下行链路RB分配示意图。其中,同一小区内不用用户的RB分配是正交的,系统整体干扰主要取决于相邻小区用户RB的分配方案。假设每个用户的信息容量可在信干比(SIR)测量值的基础上得出,则系统RB最优分配的目标是使所有用户的信息容量之和最大化。这是一个典型的NP-hard组合优化问题,所需要的计算量与覆盖范围内移动用户数的阶乘成正比。
图4 多小区多用户无线资源分配
以基于Q 学习算法的应用为例。假设某一智能实体负责上述移动用户的RB分配,则该智能实体的动作可以遵循以下原则对用户RB进行更新:1)在同一小区内,选择SIR较好的空闲RB分配给用户;2)不断根性本小区SIR最差用户的RB,以寻求更好的系统性能;3)对于同一RB,把本小区SIR最差的用户与相邻小区SIR最好的用户进行配对或分簇,如图3所示。前两个原则易于理解,而第三个原则旨在避免位置相近、且处于小区边缘的用户被分配相同的RB。此时,相邻基站无论如何调整发射功率,这些用户均无法同时获得正常工作所需的SIR。
智能实体在动作集合确定后,以所有用户的信息容量之和为最大准则,选择当前最优的动作对RB进行调整,并按照Bellman公式对Q函数进行实时更新[13]。如此迭代操作,直至Q函数趋于稳定。
上述迭代过程还应与用户的功率最优分配相结合。文献[36]基于博弈论框架,给出了多小区用户采用相同RB时的最优功率分配方法。如果系统需要进一步考虑用户QoS的比例公平性,可引入拉格朗日乘子法,构造相应的动作评估准则和Q函数。
3.3 5G通用加速器
相比于4G,5G的基带处理需要考虑更多的模块,例如:大规模MIMO检测、NOMA检测及Polar码译码等,这会使硬件面积增加,实现架构不规律。可以注意到,尽管5G基带模块众多,但所有功能均可以用基于因子图的置信传播算法实现[37-41]。针对特定的基带功能,置信传播算法只需确定变量符号集、变量间关系等参数,而保持其余的部分不变。因此可以用以个基于置信传播的、参数可配置的通用加速器实现整个基带功能。
尽管基于置信传播的算法可以实现5G通用加速器,但受其性能限制,置信传播算法在一些场景下仍然无法满足要求。为此我们尝试在置信传播算法通用加速器的基础上,实现基于AI的5G通用加速器。我们可以通过以下两种方法,将一个置信传播算法改进为一个性能良好的AI算法。
方法一:将置信传播算法改为深度神经网络。方法如下:1)将置信传播算法的因子图复制多次,并按照原有的方式连接为一个深度神经网络,复制次数等于置信传播算法的迭代次数。2)对DNN进行训练。[20]提出的基于DNN的Polar码译码器,[42]提出的基于DNN的MIMO检测器等是方法一在基带模块上实现的范例。
方法二:将置信传播算法改为卷积神经网络算法。方法如下:1)将置信传播算法的因子图节点排列在图片上,其中每个像素代表一个节点。像素相邻意味着其对应的节点在因子图上相连。2)用连接得到的图像对CNN进行训练。[43]提出的BP-CNN信道译码器应用了方法二。
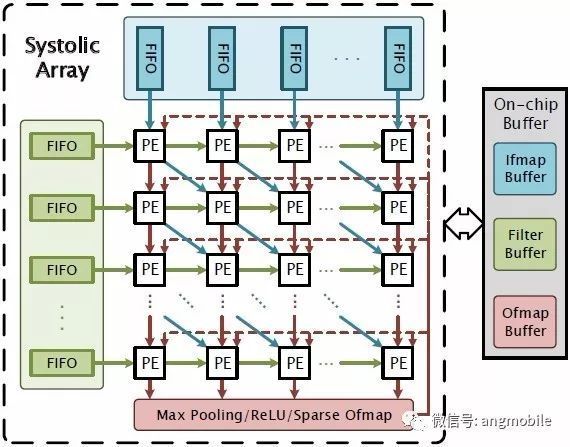
AI技术中的神经网络算法具有高度的自适应性与可靠性。通过将基带算法转化为神经网络能够处理的问题,我们受益于以下两方面:1)系统性能的提升;2)硬件架构的统一。光差神经网络的算法,我们发现:CNN核心操作是卷积运算,而DNN核心操作为二维矩阵乘法运算。二维脉冲阵列可以同时完成上述两种算法。因此利用同一脉冲阵列,只需对数据数据进行合理调度,即可同时实现CNN与DNN的功能,从而实现基于AI的5G通用加速器。文献[18]综合研究了神经网络的高效量化策略以及硬件实现。一种二维脉冲阵列架构如图5所示,可以看出其高度的鬼整形和可扩展性。
图5 神经网络的二维脉冲阵列硬件架构
文献[21]指出,在由信道编码、信道、信道均衡器以及译码器组成的系统中(如图6),接收机的均衡器与译码器分别可用CNN和DNN实现。对应的AI加速器有两种实现方案。1)硬件消耗优先的设计:我们可将整个接收机折叠为一个通用处理器。通用处理器首先工作于均衡器模式(CNN),输入为来自信道的信息,输出被保留下来;然后工作于译码器模式(DNN),将刚保存的结果作为输入,输出最后的译码结果。2)吞吐速率优先的设计:接收机由两个通用处理器组成流水线,两个处理器分别工作在均衡器和译码器模式。可以看出,相比于传统实现,通用处理器可带来更多硬件设计自由度,以更好的满足不同系统要求。
图6 包含均衡器与译码器的接收机示意
3.4 5G物理层端到端优化
AI算法在物理层若干模块上成功实现了功能优化,如:文献[44]提出的基于神经网络的调制模式识别,[20]提出的DNN极化码译码器,以及[43]提出的机遇DNN的MIMO检测算法等。在两个或多个物理层模块的联合优化问题中,AI算法也得到了成功的应用,如[21]提出的基于神经网络的信道均衡和信道译码的联合优化。但单个模块的优化并无法保证整个物理层端到端通信的整体优化[45],而端到端通信的实现中,多个基于迭代算法的AI模块的拼接反而会带来更高的训练和计算复杂度。因此,我们需要一种对物理层端到端的联合优化方法。
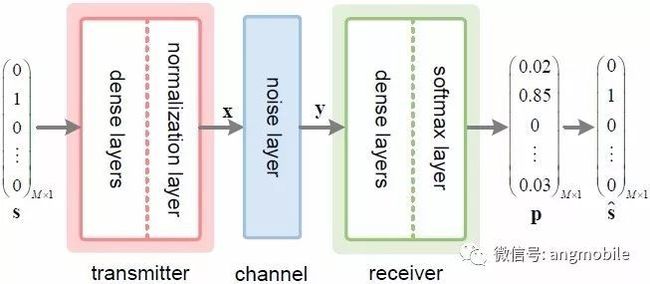
文献[46]提出将物理层通信看做一个端到端的信号重构问题,并应用自编码器概念来表示物理层通信过程,进行端到端通信的联合优化。自编码器是一种无监督深度学习算法,属于神经网络,通过学习输入信息的压缩形式来进行压缩信息的重构。在利用自编码器构建的端到端通信模型中,编码、调制、信道均衡等物理层模块,被简单表示为发射端、信道和接收端三个模块:发射端和接收端都分别表示为全连接的DNN,其中发射端连接一个归一化层来确保输出值符合物理约束,接收端侧连接一个softmax激活函数层,最后输出一个组概率向量来决定接收到的信息。两者中间的AWGN信道则用神经网络的一个噪声层(noise layer)表示,从而将通信系统表示为结构如图7所示的大型自编码器。该自编码器基于端到端的误比特率(BER)或误块率(BLER)表示进行训练,完成训练的自编码器即可基于接收信号对传输信号进行重构。
图7 用自编码器构建端到端通信模块的简单结构
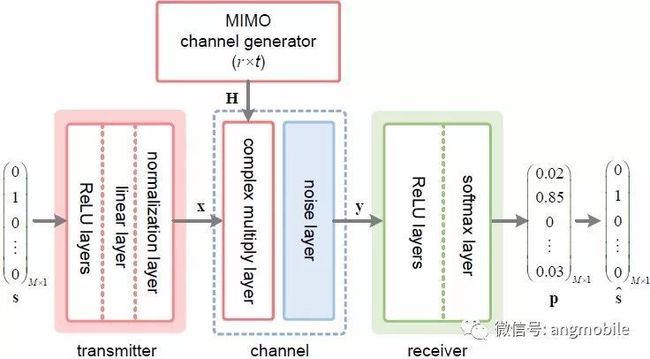
自编码器方法不基于任何经典的编码、检测方法,而是将整个端到端通信构筑为一个用于信息重构的DNN并行联合优化。在难以建立准确模型的复杂现实环境中,自编码器方法不采用经典模型,而是利用大量数据的支撑和机器学习算法的强大功能来“学习”复杂的信道状况,从而优化整个通信过程。同时,它也有效避免了多种模块拼接而产生的多层网络锁带来的高复杂度和大计算量。[46]将自编码器模型推广到干扰信道的多用户通信模型上,而[47]则将这种自编码器优化方法推广到MIMO上,通过增加信道矩阵相关模块,形成了如图8所示的MIMO自编码器通信模型。文献[46,47]的试验结果均显示自编码器方法建立了一种可用于不同CSI信息,天线数等情况下的统一物理层框架,并且在更低的计算复杂度下可通过“学习”得到比经典方法更低的误比特率。而上述端到端优化策略可以利用上文所述的“基于AI的5G通用加速器”加以实现。
图8 用自编码器构建的MIMO端到端通信模型结构
4. 结束语
5G突破了传统移动通信系统的应用范畴,在大幅提升传统移动互联网服务能力的同时,将应用的触角渗透至各行各业的物理网应用,从而演变成为支撑全社会、全行业运行的基础性互联网了。以统一的技术框架支撑极度差异化的复杂应用,5G技术的发展正面临着前所未有的挑战。AI技术的新一轮赋形及迅猛发展,为应对上述挑战并超越传统移动通信设计理念与性能提供了潜在的可能性。
AI技术在5G移动通信系统中应用,已有大量的研究文献可供借鉴。本文并非试图全面地总结该领域已有研究成果,而是希望厘清AI技术在5G系统中最优发展生命力的研究方向,并通过在这些方向上的进一步努力,使5G系统性能与实现的便利性可以显著超越传统移动通信系统。基于本文所给出的若干典型应用范例,我们有理由期待上述努力在不远的未来取得显著成效。
参考文献
1 尤肖虎,潘志文,高西奇,等. 5G移动通信发展趋势与若干关键技术. 中国科学:信息科学,2014, 44 (5):551-563
2 3GPP. RP-170741, Way Forward on the Overall 5G-NR eMBB. Workplan[s]. 2017
3 3GPP. Study on New Radio Access Technology: Radio Access Architecture and Interfaces (Release 14). TR38.801, v14.0[s]. 2017
4 ITU-R. Minimum Requirements Related to Technical Performance for IMT2020 Radio Interface(s). Report ITU-R M.2410-0. 2017
5 3GPP. Release-15: LTE Enhancements and 5G Normative Work. 2018
6 You X H, Wang D M, Sheng B, et al. Cooperative distributed antenna systems for mobile communications. IEEE Wirel Commun, 2010, 17(3): 35
7 Yang W J, Wang M, Zhang J J, et al. Narrowband wireless access for low-power massive Internet of things: A bandwidth perspective. IEEE Wirel Commun, 2017, 24(3): 138-145
8 Whitley D. A genetic algorithm tutorial. Stat Comput, 1994, 4(2): 65-85
9 Schmidhuber J. Deep learning in neural networks: An overview. Neural Netw, 2015, 61: 85-117
10 Yu (You) X H. Can backpropagation error surface not have local minima. IEEE T Neural Networ, 1992, 3(6): 1019-1021
11 Yu (You) X H, Chen G A, Cheng S X. Dynamic learning rate optimization of the backpropagation algorithm. IEEE T Neural Networ, 1995, 6(3): 669-677
12 Yu (You) X H, Chen G A. Efficient backpropagation learning using optimal learning rate and momentum. Neural Netw, 1997, 10(3): 517-527
13 Kaelbling L P, Littman M L, Moore A W. Reinforcement learning: A survey. J Artif Intell Res, 1996, 4: 237-285
14 Watkins C J C H, Dayan P. Q-learning. Mach Learn, 1992, 8(3-4): 279-292
15 Gatherer A. Machine learning Modems: How ML will change how we specify and design next generation communication systems. IEEE ComSoc News, 2018.
16 Yang C, Xu W H, Zhang Z C, et al. A channel-blind detection for SCMA based on image processing techniques. In: Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS), 2018: 1-5
17 Zhang C, XuWH. Neural networks: Efficient implementations and applications. In: Proceedings of IEEE International Conference on ASIC (ASICON), 2017: 1029-1032
18 Xu W H, You X H, Zhang C. Efficient deep convolutional neural networks accelerator without multiplication and retraining. In: Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2018: 1-5
19 Xu W H, Wang Z F, You X H, et al. Efficient fast convolution architectures for convolutional neural network. In: Proceedings of IEEE International Conference on ASIC (ASICON), 2017: 904-907 20 Xu W H, Wu Z Z, Ueng Y L, et al. Improved polar decoder based on deep learning. In: Proceedings of IEEE International Workshop on Signal Processing Systems (SiPS), 2017:1-6
21 Xu W H, Zhong Z W, Be’ery Y, et al. Joint neural network equalizer and decoder. In: Proceedings of IEEE International Symposium on Wireless Communication Systems (ISWCS), 2018:1-6
22 Xu W H, Be’ery Y, You X H, et al. Polar decoding on sparse graphs with deep learning. In: Proceedings of Asilomar Conference on Signals, Systems, and Computers (Asilomar), 2018:1-6
23 Xu W H, You X H, Zhang C. Using Fermat number transform to accelerate convolutional neural network. In: Proceedings of IEEE International Conference on ASIC (ASICON), 2017: 1033-1036
24 Gao X Q, Jiang B, Li X, et al. Statistical eigenmode transmission over jointly-correlated MIMO channels. IEEE T Inform Theory, 2009,55 (8): 3735-3750
25 Wang D M, Zhang Y, Wei H, et al. An overview of transmission theory and techniques of large-scale antenna systems for 5G wireless communications. Sci China Inform Sci, 2016, 59(8): 081301
26 Gesbert D, Hanly S, Huang H, et al. Multi-cell MIMO cooperative networks: A new look at interference. IEEE J Sel Area Comm, 2010, 28(9): 1380-1408
27 Jing S S, Yu A L, Liang X, et al. Uniform belief propagation processor for massive MIMO detection and GF (2n) LDPC decoding. In: Proceedings of IEEE International Conference on ASIC (ASICON), 2017: 961-964
28 Gandhi V S, Maheswaran B. A cross layer design for performance enhancements in LTE-A system. In: Proceedings of IEEE International Conference on Wireless Communications, Signal Processing and Networking (WiSPNET), 2016: 905-909
29 Kuen J, Kong X F, Wang G, et al. DelugeNets: Deep networks with efficient and flexible cross-layer information inflows. In: Proceedings of IEEE International Conference on Computer Vision Workshop (ICCVW), 2017: 958-966
30 Farsad N, Rao M, Goldsmith A. Deep learning for joint source-channel coding of text. arXiv preprint, 2018.
31 Xu X W, Ding Y K, Hu S X, et al. Scaling for edge inference of deep neural networks. Nature Electronics, 2018, 1(4):216
32 Wang X F, Li X H, Leung V C M. Artificial intelligence-based techniques for emerging heterogeneous network: State of the arts, opportunities, and challenges. IEEE Access, 2015, 3: 1379-1391
33 Klaine P V, Imran M A, Onireti O, et al. A Survey of machine learning techniques applied to self-organizing cellular networks. IEEE Commun Surv Tut, 2017, 19(4): 2392-2431
34 P`erez-Romero J, Sallent O, Ferr ú s R, et al. Knowledge-based 5G radio access network planning and optimization. In: Proceedings of IEEE International Symposium on Wireless Communication Systems (ISWCS), 2016: 359-365
35 G′omez-Andrades A, Munoz P, Serrano I, et al. Automatic root cause analysis for LTE networks based on unsupervised techniques. IEEE T Veh Technol, 2016, 65(4): 2369-2386
36 Wang J H, Guan W, Huang Y M, et al. Distributed optimization of hierarchical small cell networks: A GNEP framework. IEEE J Sel Area Comm, 2017, 35(2): 249-264
37 Ren Y R, Zhang C, Liu X, et al. Efficient early termination schemes for belief-propagation decoding of polar codes. In: Proceedings of IEEE International Conference on ASIC (ASICON), 2015: 1-4
38 Fossorier M P C, Mihaljevic M, Imai H. Reduced complexity iterative decoding of low-density parity check codes based on belief propagation. IEEE T Commun, 1999, 47(5): 673-680
39 Yang J M, Song W Q, Zhang S Q, et al. Low-complexity belief propagation detection for correlated large-scale MIMO systems. J Signal Process Sys, 2018, 90(4): 585-599
40 Liu L, Yuen C, Guan Y L, et al. Gaussian message passing iterative detection for MIMO-NOMA systems with massive access. In: Proceedings of IEEE Global Communications Conference (GLOBECOM), 2016: 1-6
41 Yang J M, Zhang C, Zhou H Y, et al. Pipelined belief propagation polar decoders. In: Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS), 2016: 413-416
42 Tan X S, Xu W H, Be’ery Y, et al. Improving massive MIMO belief propagation detector with deep neural network.
43 Liang F, Shen C, Wu F. An iterative BP-CNN architecture for channel decoding. IEEE J Sel Top Signa, 2018, 12(1): 144-159
44 Lv X Z, Wei P, Xiao X C. Automatic identification of digital modulation signals using high order cumulants. Electronic Warfare, 2004, 6:1
45 Wang T Q, Wen C K, Wang H Q, et al. Deep learning for wireless physical layer: Opportunities and challenges. China Commun, 2017, 14(11): 92-111
46 O’Shea T, Hoydis J. An introduction to deep learning for the physical layer. IEEE Trans on Cogn Commun Netw, 2017, 3(4): 563-575
47 O’Shea T J, Erpek T, Clancy T C. Deep learning based MIMO communications. arXiv preprint, 2017.