机器学习-支持向量机(python3代码实现)

支持向量机

哈尔滨工程大学-537

算法原理：

一、寻找最大间隔

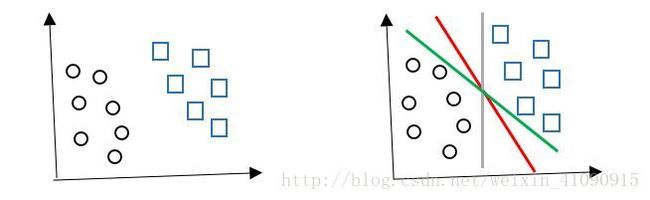
如下图所示，用一条分割线将两类点分割开来(二维的是一条分割线，多维的就是分隔面)，显然三条线都能将两类点分割开来，然而，从直观来看，红色的分割线显然分割效果最好。为什么这么说呢？

因为红色的分割线到两边最近的点的距离更远。可以直观把两边的两类点想象成地雷，我们有一支红军要通过这片雷区，显然，沿着绿色和灰色的路线行军，两边不会踩到地雷的安全区域非常的窄，而沿着红色的路线行军，安全区域明显更宽。我们的目的就是要找到能够使安全区域最宽的行军路线，最终使红军夺得革命战争的胜利。

如下图所示，距离分割线最近的几个点的位置，决定了分割线的位置，形象的来说，就是距离红军队伍最近的几个地雷的位置，决定了红军穿过雷区的行军路线，如果距离红军最近的地雷的位置发生改变，红军的行军路线就必须随之改变，否则安全区域就有可能变窄，踩到地雷的可能性就会增加。

那么此时要解决的目标就非常明确了，即找到距离分割线最近的那几个点，而这几个距离分割线最近的点，就叫做支持向量，这就是支持向量机一词的由来。
那么如何找到距离分割线最近的那几个点？

由高中数学可知：空间中一个点 (x1,y1,z1) ( x 1 , y 1 , z 1 ) 到平面线 ax+by+cz+d=0 a x + b y + c z + d = 0 的距离为： ax1+by1+cz1+da2+b2+c2√ a x 1 + b y 1 + c z 1 + d a 2 + b 2 + c 2 ；

扩展为多维的情况，点 Xi=(xi1,xi2...xik) X i = ( x i 1 , x i 2 . . . x i k ) 到一个超平面 WTX+b=0 W T X + b = 0 的距离为： WTXi+b||W|| W T X i + b | | W | | ，其中 W W 和 X X 为 k k 维向量(因为 Xi X i 有 k k 个特征)。

于是当前的任务就是要找到 WTXi+b||W|| W T X i + b | | W | | 值最小的数据点，将该点的 WTXi+b||W|| W T X i + b | | W | | 最大化，此时的 W W 和 b b 就是我们要找的最优分割超平面的参数。

由高中数学可知：若点 (x1,y1) ( x 1 , y 1 ) 在直线 y=ax+b y = a x + b 的上侧，则将点 (x1,y1) ( x 1 , y 1 ) 带入直线得 ax1+b−y1>0 a x 1 + b − y 1 > 0 ，反之，若在下侧，则带入直线得 ax1+b−y1<0 a x 1 + b − y 1 < 0 ;

推广到多维的情况：若数据点 Xi X i 在超平面正侧， WTXi+b>0 W T X i + b > 0 ，那么将在这一侧的数据点定义为1类，即类别标签 yi y i 为1，那么 yi(WTXi+b)>0 y i ( W T X i + b ) > 0 ；
反之，若数据点 Xi X i 在超平面的负侧， WTXi+b<0 W T X i + b < 0 ,那么将这一侧的数据点定义为-1类，即类别标签 yi y i 为-1，那么 yi(WTXi+b)>0 y i ( W T X i + b ) > 0 ， 这样在比较大小的时候，就避免了负数的出现。

那么此时，首要任务就是找到 yi(WTXi+b)||W|| y i ( W T X i + b ) | | W | | 最小的数据点，并将该点的 yi(WTXi+b)||W|| y i ( W T X i + b ) | | W | | 值最大化。

若限制 yi(WTXi+b)≥1 y i ( W T X i + b ) ≥ 1 ，则距离超平面最近的点的 yi(WTXi+b) y i ( W T X i + b ) 应等于1，而 ||W|| | | W | | 则越大，说明该点离超平面越近。

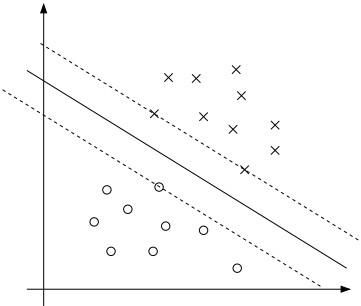
如下图，可以更加直观的理解以上说法，虚线 WTX+b−1=0 W T X + b − 1 = 0 和虚线 WTX+b+1=0 W T X + b + 1 = 0 分别是两条与直线 WTX+b=0 W T X + b = 0 平行的直线(由高中数学可知, WTX+b−1=0 W T X + b − 1 = 0 在直线上侧， WTX+b+1=0 W T X + b + 1 = 0 在直线下侧)，通过归一化系数W，可以使最后的常数一直保持+1和-1，也就是说，这两条虚线可以在平面上任意移动，而始终保持 WTX+b−1=0 W T X + b − 1 = 0 和 WTX+b+1=0 W T X + b + 1 = 0 的形式。那么现在的要求就是，让这两条虚线之间的距离最大，且要保证所有点都在这两条虚线之外(或在虚线之上)，即1类样本点都在 WTX+b−1=0 W T X + b − 1 = 0 的正侧(或在线上)，即 WTXi+b−1≥0 W T X i + b − 1 ≥ 0 ；而-1类样本点都在 WTX+b+1=0 W T X + b + 1 = 0 的负侧(或在线上)，即 WTXi+b+1≤0 W T X i + b + 1 ≤ 0 。

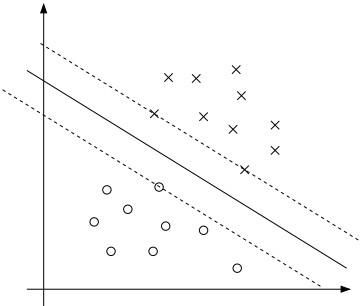
如果把+1和-1项都移到等式右边，就分别为： WTXi+b≥+1 W T X i + b ≥ + 1 和 WTXi+b≤−1 W T X i + b ≤ − 1 ，再分别乘上它们的类别标签 yi y i ，就可以用一个式子来表示了，即 WTXi+b≥1 W T X i + b ≥ 1 。

那么此时的首要任务可以这样表述：给定训练样本 (Xi,yi) ( X i , y i ) ，在 yi(WTXi+b)≥1 y i ( W T X i + b ) ≥ 1 的限制条件下，使 yi(WTXi+b)||W|| y i ( W T X i + b ) | | W | | 尽可能的大。

而能对分割超平面产生影响的只有支持向量，即位于虚线上的样本点，即 yi(WTXi+b)=1 y i ( W T X i + b ) = 1 的样本点，那么此时只需要使分母，即 ||W|| | | W | | 尽可能的大，为了后面计算方便，改写为使 12||W|| 1 2 | | W | | 即 12WTW 1 2 W T W 尽可能的大。此时的 W W 和 b b 就是最优超平面的参数。

由高数内容可知：带限制条件的求极值，可以应用拉格朗日乘子法。即求 12WTW 1 2 W T W 的极值，限制条件为 1−yi(WTXi+b)≤0 1 − y i ( W T X i + b ) ≤ 0 (拉格朗日乘子法要求限制条件为 f(x)≤0 f ( x ) ≤ 0 的形式)。由于对于每一个数据点 Xi(i=1,2...n) X i ( i = 1 , 2... n ) ，都作此限定条件，即任意的 1−yi(WTXi+b)≤0 1 − y i ( W T X i + b ) ≤ 0 ， (i=1,2...n) ( i = 1 , 2... n ) 。

于是由拉格朗日乘子法得：

L(W,α,,b)=12WTW+∑i=1nαi(1−yi(WTXi+b)) L ( W , α , , b ) = 1 2 W T W + ∑ i = 1 n α i ( 1 − y i ( W T X i + b ) )

要求什么样的 W W 和 b b 能使 L(W,α,b) L ( W , α , b ) 取得极小值，应分别对 W W 和 b b 求导，使导数为0，于是得到：

∂L∂W=W−∑i=1nαiyiXi=0 ∂ L ∂ W = W − ∑ i = 1 n α i y i X i = 0

∂l∂b=∑i=1nαiyi=0 ∂ l ∂ b = ∑ i = 1 n α i y i = 0

于是可得：

W=∑i=1nαiyiXi W = ∑ i = 1 n α i y i X i

首先将 L(W,α,b) L ( W , α , b ) 逐项展开，得到：

L(W,α,b)=12WTW+∑i=1nαi−∑i=1nαiyiWTXi−b∑i=1nαiyi L ( W , α , b ) = 1 2 W T W + ∑ i = 1 n α i − ∑ i = 1 n α i y i W T X i − b ∑ i = 1 n α i y i

再将 W W 带回到 L(W,α,b) L ( W , α , b ) 中，并且 ∑ni=1αiyi=0 ∑ i = 1 n α i y i = 0 ，得到：

12(∑i=1nαiyiXi)T(∑i=1nαiyiXi)+∑i=1nαi−∑i=1nαiyi(∑i=1nαiyiXi)TXi 1 2 ( ∑ i = 1 n α i y i X i ) T ( ∑ i = 1 n α i y i X i ) + ∑ i = 1 n α i − ∑ i = 1 n α i y i ( ∑ i = 1 n α i y i X i ) T X i

整理后可得：

J(α)=∑i=1nαi−12∑i=1n∑j=1nαiαjyiyj(Xi)TXi J ( α ) = ∑ i = 1 n α i − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j ( X i ) T X i

于是得到此时的目标函数为 J(α) J ( α ) 。即这样的 W W 和 b b 能够使得 L(W,α,b) L ( W , α , b ) 取得极小值，并且将 W W 和 b b 带入 L(W,α,b) L ( W , α , b ) 后得到 J(α) J ( α ) ，现在的目标是将 J(α) J ( α ) 最大化。并且限制条件为：

∑i=1nαiyi=0 ∑ i = 1 n α i y i = 0

αi≥0 α i ≥ 0

式子 J(α) J ( α ) 中的 Xi,yi X i , y i 是全体样本点，然而 J(α) J ( α ) 取得极大值仅仅依赖距离超平面最近的点，即只和支持向量有关。所以 J(α) J ( α ) 的解必然是稀疏的，即对于支持向量， α>0 α > 0 ，而对于其他样本点， α=0 α = 0 。

故将样本点带入 J(α) J ( α ) ，再分别对 αi α i 求导，使导数等于0，再根据 ∑ni=1αiyi=0 ∑ i = 1 n α i y i = 0 ,求解 αi α i ，且 αi α i 需满足限定条件 αi≥0 α i ≥ 0 。

若解不满足限定条件，则解可能在限制边界上，则将将其中一个 α α 以0带入，求解其他 α α 值

再根据式子： W=∑ni=1αiyiXi W = ∑ i = 1 n α i y i X i ，求解出 W W 。
最后根据式子 yi(WTXi+b)=1 y i ( W T X i + b ) = 1 ，求解出 b b 。
于是便得到了最优超平面的参数 W W 和 b b 。

二、引入松弛变量

以上是针对比较完美的情况，即两类点100%线性可分，但是如果数据点并没有那么“干净”，这时候就可以引入所谓“松弛变量”，来允许有些数据点可以处于分割面的错误一侧，此时，限制条件为：

yi(WTXi+b)≥1−ξi y i ( W T X i + b ) ≥ 1 − ξ i

ξi≥0 ξ i ≥ 0

之前是使得 12WTW 1 2 W T W 取极小值，现在是是使 12WTW+C∑ni=1ξi 1 2 W T W + C ∑ i = 1 n ξ i 取得极小值。这里的 C C 是可调节的参数，当 C C 比较大时，显然 ξi ξ i 比较小； C C 比较小时，则 ξi ξ i 比较大。

于是此时应用拉格朗日乘子法可得：

L(W,b,ξi,α,μ)=12WTW+C∑i=1nξi+∑i=1nαi(1−ξi−yi(WTXi+b))−∑i=1nμiξi L ( W , b , ξ i , α , μ ) = 1 2 W T W + C ∑ i = 1 n ξ i + ∑ i = 1 n α i ( 1 − ξ i − y i ( W T X i + b ) ) − ∑ i = 1 n μ i ξ i

(这里将 ξi≥0 ξ i ≥ 0 变成 −ξi≤0 − ξ i ≤ 0 的形式，以适用拉格朗日乘子法)

与之前同样的做法，求 L(W,b,ξi,α,μ) L ( W , b , ξ i , α , μ ) 取得极小值，应对 W W ， b b ，以及引入的“松弛变量” ξi ξ i 分别求偏导 (i=1,2...n) ( i = 1 , 2... n ) ，可以看出对 W W 和 b b 求偏导结果没有改变，因此仍然可得：

W=∑i=1nαiyiXi W = ∑ i = 1 n α i y i X i

以及

∑i=1nαiyi=0 ∑ i = 1 n α i y i = 0

带入整理后仍然可得：

J(α)=∑i=1nαi−12∑i=1n∑j=1nαiαjyiyj(Xi)TXi J ( α ) = ∑ i = 1 n α i − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j ( X i ) T X i

而对 ξi(i=1,2...n) ξ i ( i = 1 , 2... n ) 分别求偏导得到：

C−αi−μi=0 C − α i − μ i = 0

此时的任务仍然是使 J(α) J ( α ) 最大化，而此时的限制条件为：

∑i=1nαi=0 ∑ i = 1 n α i = 0

αi≥0 α i ≥ 0

μi≥0 μ i ≥ 0

C−αi−μi=0 C − α i − μ i = 0

后三个限制条件可以合并为一个限制条件：

0≤αi≤C 0 ≤ α i ≤ C

于是此时便可以与之前同样的解法求解 αi α i ，唯一不同的是， αi α i 的值被限定为小于一个设定的常数C。

三、SMO求解算法(简化版)

现在的问题是如何求解 αi(i=1,2...n) α i ( i = 1 , 2... n ) ，(显然有多少个样本点，就有多少个 α α )，大神Platt给出了SMO算法进行求解，这里可以跟随实际的python代码，一行一行的分析SMO算法的原理，由于代码较复杂，在代码中敲大量注释影响代码清晰性，所以在代码之外进行相应的解释。

1）该段代码进行需要的各种库的导入，最后一行%matplotlib inline是为了保证在jupyter notebook 的运行环境下能够在浏览器上输出绘制的图像。

import numpy as np
import random
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline    

2）然后用pandas读取txt文件，并调用head方法显示文件的前几行。

file_name = r"D:\python_data\MachineLearningInaction\machinelearninginaction\Ch06\testSet.txt"
file = pd.read_table(file_name,header=None, names=["factor1","factor2","class"])
file.head()

3）可以看到所读取的txt文件的前几行如下图，每个样本有2个特征，类标签分别为+1或-1。

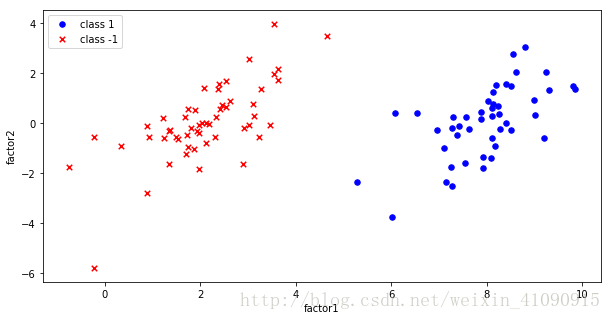
4）接下来再绘制一张样本点分布的散点图，蓝色的是正例，即+1类的点；红色的是负例，即-1类的点。横坐标为“factor1”，纵坐标为“factor2”。

positive = file[file["class"] == 1]
negative = file[file["class"] == -1]
fig, ax = plt.subplots(figsize=(10,5))
ax.scatter(positive["factor1"], positive["factor2"], s=30, c="b", marker="o", label="class 1")
ax.scatter(negative["factor1"], negative["factor2"], s=30, c="r", marker="x", label="class -1")
ax.legend()
ax.set_xlabel("factor1")
ax.set_ylabel("factor2")

5）运行后，在浏览器上输出了如下的图像。

6）现在对数据已经有了清晰直观的了解，接下来需要把pandas读取出来的整个表格进行切分，前2列作为样本点的特征矩阵，最后一列作为类标签向量。下面函数输入的是pandas都取出来的文件file，调用as_matrix方法将其转化为矩阵orig_data，将这个矩阵去除最后一列的部分作为样本点的特征矩阵data_mat，而最后一列作为类标签向量label_mat。

def load_data_set(file):
    orig_data = file.as_matrix()   
    cols = orig_data.shape[1]
    data_mat = orig_data[:,0:cols-1]
    label_mat = orig_data[:,cols-1:cols]
    return data_mat, label_mat

7）接下来调用该函数，得到样本点的特征矩阵data_mat和对应的类标签向量label_mat。

data_mat, label_mat = load_data_set(file) 

8）还需要定义一个select_jrand函数，该函数的功能是给定输入i和m，随机输出一个0到m之间的与i不同的整数。这个函数在后面将会用到。

def select_jrand(i, m):
    j = i
    while(j==i):
        j = int(random.uniform(0,m))
    return j

9）此外还需要定义一个clip_alpha函数，该函数的功能是输入将aj限制在L和H之间

def clip_alpha(aj, H, L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj

10）接下来是主体功能的实现函数，由于这个函数太长，为了方便理解，将以下代码分成一小段一小段的，这样就可以理解每一小段的功能。

10.1）循环外的初始化工作：首先该函数的输入为特征矩阵、类标签向量，常数C，容错率，最大迭代次数。首先将输入的特征矩阵和类标签向量都转化为矩阵(若特征矩阵和类标签向量已经是矩阵，则不需要这个步骤，若输入的是列表的形式，则需要该步骤)，设置b为0，m和n分别为特征矩阵的行数和列数。创建一个m行1列的 α α 向量(即有多少个样本点就有多少个 α α )，迭代次数初始化为0(每次迭代在 α α 向量中寻找一对可以改变的 α α ，若没有找到则迭代次数+1，达到最大迭代次数还没有找到可以改变的 α α ，说明已经 α α 已经优化的差不多了，则退出循环)。

10.2）内循环的初始化工作：现在开始第一轮迭代，将改变的一对 α α 的数量alpha_pairs_changed初始化为0，然后遍历m个 α α 依次作为第一个 α α ，再在(0,m)范围内随机的找到第二个 α α (第二个 α α 与第一个不能是同一个，这就用到了之前定义的select_jrand函数)。

10.3)第一小段代码：首先从i等于0开始，已知公式 W=∑niαiyiXi W = ∑ i n α i y i X i ，若第0号数据点是支持向量，则该数据点必然在虚线 WTX+b+1=0 W T X + b + 1 = 0 或 WTX+b−1=0 W T X + b − 1 = 0 上，即 WTX+b=−1 W T X + b = − 1 或 WTX+b=+1 W T X + b = + 1 。

先将0号数据点带入公式求出 W W ，即代码中的WT_i，再将0号数据点和求得的 W W 带入 WTX+b W T X + b 求出 WTX+b W T X + b 的值，即代码中的f_xi。

代码中的E_i为得到的f_xi与实际的 WTX+b W T X + b 之间的误差，而这个误差大有说道，最完美的情况是若数据点是支持向量，则将数据点带入 WTX+b W T X + b 应该等于-1或+1，即该数据点应该在虚线 WTX+b+1=0 W T X + b + 1 = 0 或虚线 WTX+b−1=0 W T X + b − 1 = 0 上，而如果该数据点的类标签 yi y i 和误差E_i的乘积大于容错率，说明该数据点属于+1类且在 WTX+b−1=0 W T X + b − 1 = 0 的上侧，或者该数据点属于-1类且在 WTX+b+1=0 W T X + b + 1 = 0 的下侧。也就是说该点在属于自己的那一类的群体里，但是太靠后了且靠后的超过限度了(即大于容错率)，根本无法作为支持向量，而这个点对应的 α α 值又大于0，说明这明明就不该是靠后站的，那么就要调整这个数据点的 α α 了。而另一种情况是该数据点的类标签 yi y i 和误差E_i的乘积小于负容错率，说明该点太靠前了已经处于虚线 WTX+b+1 W T X + b + 1 和虚线 WTX+b−1 W T X + b − 1 之间了，且该点的 α α 值又小于常数C，说明该点也不应该是靠前的，那就要调整这个数据点的 α α 了

若经过上述判断，决定要调整该数据点的 α α ，那么就调用之前定义的select_jrand函数随机的选择另一个要调整的 α α ，对另一个 alpha a l p h a 对应的数据点也计算相应的误差E_j，为了记录 α α 的调整情况，分别copy一下作为 αi α i 和 αj α j 的旧值。

10.4）第二小段代码：由于有一个限制条件即 ∑niαiyi=0 ∑ i n α i y i = 0 ，且任意的 α α 在(0,C)之间，所以当调整其中一个 αi α i 的时候，另一个 αj α j 的改变必须有一定限制，即 yiαi+yjαj=k y i α i + y j α j = k 。即如下图： αi α i 和 αj α j 必须在两条线段上。

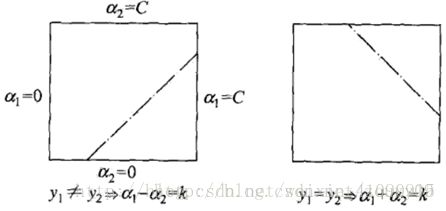
根据上图，可以得到 αj α j 的取值范围(L,H)。

10.5）第三小段代码：下面为 αj α j 的更新公式：

αj=αj−yj(Ei−Ej)η α j = α j − y j ( E i − E j ) η

其中 η=2<Xi,Xj>−<Xi,Xi>−<Xj,Xj> η = 2 < X i , X j > − < X i , X i > − < X j , X j > 。(尖括号表示两个向量的内积)
更新前先对 η η 进行判断，若 η≥0 η ≥ 0 则退出本次循环，不进行更新。否则对 αj α j 进行更新。更新后需要调用之前定义的clip_alpha函数，将更新后的 αj α j 缩小在这个范围之内，最后检验一下 αj α j 值改变了多少，如果改变的太少，就不要更新了，直接退出本次循环寻找下一对 α α ，改变那点值没什么意义。
最后既然 αj α j 更新了， αi α i 也得随之改变，且该变量应该是相等的，根据之前所述的 yiαi+yjαj=k y i α i + y j α j = k ，可以得到更新后的 αi α i 的值。

10.6）第四小段代码：对于样本点i，已经更新了其 αi α i 值，若b值也是正确的，则该点应该从更新之前的不在 WTX+b±1=0 W T X + b ± 1 = 0 上，更新到位于 WTX+b±1=0 W T X + b ± 1 = 0 上，亦即将样本点i带入，得到 Enewi=WnewTXi+bnew−yi=0 E i n e w = W n e w T X i + b n e w − y i = 0 。
同时又已知 Eoldi=WoldTXi+bold−yi E i o l d = W o l d T X i + b o l d − y i ，根据上述两个公式，可以得到：

bnew=bold−Eoldi+WoldTXi−WnewTXi b n e w = b o l d − E i o l d + W o l d T X i − W n e w T X i

前两项不用多说，最后两项的相减，有些说道，因为 W=∑ni=1αiyiXi W = ∑ i = 1 n α i y i X i ，所以其实 Wold W o l d 和 Wnew W n e w 的区别只在里面的 αiyiXi α i y i X i 和 αjyjXj α j y j X j 不同，只要把公式展开成向量的形式写出来就很容易看出来，二者相减之后的结果就是:

yi(αiold−αinew)<Xi,Xi>+yj(αoldj−αnewj)<Xj,Xi> y i ( α i o l d − α i n e w ) < X i , X i > + y j ( α j o l d − α j n e w ) < X j , X i >

将后两项带入，就可以得到 bnew b n e w 。
当然这里得到的是根据样本点i求得的 bnew b n e w ，根据样本点j做同样操作，可以得到另一个 bnew b n e w ，此时若更新后的 αi α i 在限定范围内，则 b=bnew1 b = b 1 n e w ,若 αj α j 在限定范围内，则 b=bnew2 b = b 2 n e w ，若 αi α i 和 αj α j 都在限定范围内，则 b=b1+b22 b = b 1 + b 2 2 。

10.7)收尾工作：若程序运行到此处，则已经更新了一对 α α ，并且也更新了 b b 值，则将alpha_pairs_changed加上1，代表更新了一对，继续更新下一对。若程序没有执行更新 α α 的操作，即alpha_pairs_changed=0，则将iter+1，代表迭代了一次，否则将iter置为1，重新开始迭代。若程序迭代的次数达到了最大迭代次数，还没有 α α 被更新，说明已经更新的很好了，则可以退出while循环，返回b值和 α α 向量。

def smo_simple(data_mat, class_label, C, toler, max_iter):
    # 循环外的初始化工作
    data_mat = np.mat(data_mat); label_mat = np.mat(class_label) 
    b = 0
    m,n = np.shape(data_mat)  
    alphas = np.zeros((m,1))       
    iter = 0    
    while iter < max_iter:
        # 内循环的初始化工作
        alpha_pairs_changed = 0
        for  i in range(m):   
            # 第一小段代码  
            WT_i = np.dot(np.multiply(alphas, label_mat).T, data_mat)  
            f_xi = float(np.dot(WT_i, data_mat[i,:].T)) + b   
            Ei = f_xi - float(label_mat[i])    
            if((label_mat[i]*Ei < -toler) and  (alphas[i] < C)) or \
            ((label_mat[i]*Ei > toler) and (alphas[i] > 0)):  
                j = select_jrand(i, m) 
                WT_j = np.dot(np.multiply(alphas, label_mat).T, data_mat)
                f_xj = float(np.dot(WT_j, data_mat[j,:].T)) + b    
                Ej = f_xj - float(label_mat[j])    
                alpha_iold = alphas[i].copy()
                alpha_jold = alphas[j].copy()

               # 第二小段代码
                if (label_mat[i] != label_mat[j]):  
                    L = max(0, alphas[j] - alphas[i])  # 
                    H = min(C, C + alphas[j] - alphas[i])
                else:                              
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if H == L :continue

                # 第三小段代码
                eta = 2.0 * data_mat[i,:]*data_mat[j,:].T - data_mat[i,:]*data_mat[i,:].T - \
                data_mat[j,:]*data_mat[j,:].T
                if eta >= 0: continue
                alphas[j] = (alphas[j] - label_mat[j]*(Ei - Ej))/eta
                alphas[j] = clip_alpha(alphas[j], H, L)   
                if (abs(alphas[j] - alpha_jold) < 0.00001):
                    continue


                alphas[i] = alphas[i] + label_mat[j]*label_mat[i]*(alpha_jold - alphas[j])

                # 第四小段代码
                b1 = b - Ei + label_mat[i]*(alpha_iold - alphas[i])*np.dot(data_mat[i,:], data_mat[i,:].T) +\
                label_mat[j]*(alpha_jold - alphas[j])*np.dot(data_mat[i,:], data_mat[j,:].T)
                b2 = b - Ej + label_mat[i]*(alpha_iold - alphas[i])*np.dot(data_mat[i,:], data_mat[j,:].T) +\
                label_mat[j]*(alpha_jold - alphas[j])*np.dot(data_mat[j,:], data_mat[j,:].T)
                if (0 < alphas[i]) and (C > alphas[i]):
                    b = b1
                elif (0 < alphas[j]) and (C > alphas[j]):
                    b = b2
                else:
                    b = (b1 + b2)/2.0
                alpha_pairs_changed += 1
        if (alpha_pairs_changed == 0): iter += 1
        else: iter = 0
    return b, alphas

11）接下来调用该函数，得到b值和 α α 向量，由于 α α 的值大多为0，所以只打印大于零的 α α 值。

b, alphas = smo_simple(data_mat, label_mat, 0.6, 0.001, 10)
print(b, alphas[alphas>0])

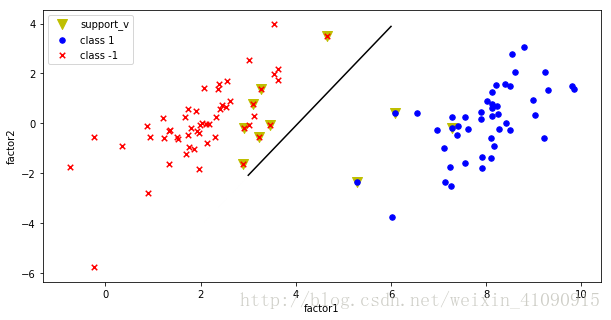
12）辛辛苦苦走到这里，就看到几个所谓的 α α 和一个b值，真的不够。“锦瑟无端五十弦，一弦一柱思华年”，每一个算法的推导，每一段代码的理解，都给我留下了深刻的印象。过程的享受是一种润物无声的细腻，但我想要的更是成功之后那会“当凌绝顶，一览众山小”的快意，更要那“冲天香阵透长安，满城尽戴黄金甲”的震撼。于是，我又敲下了如下代码，得到了，那虽不太完美，却凝聚了我心血的分、割、线。

support_x = []
support_y = []
class1_x = []
class1_y = []
class01_x = []
class01_y = []
for i in range(100):
    if alphas[i] > 0.0:
        support_x.append(data_mat[i,0])
        support_y.append(data_mat[i,1])        
for i in range(100):
    if label_mat[i] == 1:
        class1_x.append(data_mat[i,0])
        class1_y.append(data_mat[i,1])
    else:
        class01_x.append(data_mat[i,0])
        class01_y.append(data_mat[i,1])       
w_best = np.dot(np.multiply(alphas, label_mat).T, data_mat)
fig, ax = plt.subplots(figsize=(10,5))
ax.scatter(support_x, support_y, s=100, c="y", marker="v", label="support_v")
ax.scatter(class1_x, class1_y, s=30, c="b", marker="o", label="class 1")
ax.scatter(class01_x, class01_y, s=30, c="r", marker="x", label="class -1")
lin_x = np.linspace(3,6)
lin_y = (-float(b) - w_best[0,0]*lin_x) / w_best[0,1]
plt.plot(lin_x, lin_y, color="black") 
ax.legend()
ax.set_xlabel("factor1")
ax.set_ylabel("factor2")

+++++++++++刚好在这一刻，2018年的蓝色月全食发生了+++++++++++++++
++++++向月全食致敬，祝我一年好运气，2018.1.31，19：41月全食++++++++