机器学习-K均值聚类(python3代码实现)

K均值聚类

哈尔滨工程大学-537

算法原理：

K均值是发现给定数据集的 k k 个簇的算法。簇个数 k k 是用户给定的，每一个簇通过其质心(centroid)，即簇中所有点的中心来描述。

K均值算法的工作流程是：首先随机确定 k k 个初始点作为质心。然后将数据集中的每个点分配到一个簇，具体来讲，为每个点找距其最近的质心，并将其分配给该之心所对应的簇。这一步完成后，每个簇的质心更新为该簇所有点的平均值。

代码实现 ：

一、基础实现

1）首先导入所需要的各个库
%matplotlib inline是为了使接下来的绘图能够显示在Jupyter notebook的浏览器上。

import numpy as np
import math
import matplotlib.pyplot as plt
%matplotlib inline

2）定义加载样本点数据的函数load_dataset，输入参数为文件名；
将文件按行读取，每一行为一个列表，依次追加到空列表data_mat中，最后以矩阵的形式返回所得。

def load_dataset(file_name):
    data_mat = []
    with open(file_name) as fr:
        lines = fr.readlines()
    for line in lines:
        cur_line = line.strip().split("\t")
        flt_line = list(map(lambda x:float(x), cur_line))
        data_mat.append(flt_line)
    return np.array(data_mat)

3）调用load_dataset函数，参数为将要打开的文件的路径和文件名，得到样本点的特征矩阵矩阵data_set。

data_set = load_dataset(r"D:\python_data\MachineLearningInaction\machinelearninginaction\Ch10\testSet.txt")
print(data_set)

将其打印出来，得到一个80行，2列的矩阵，其中前9行如下图：

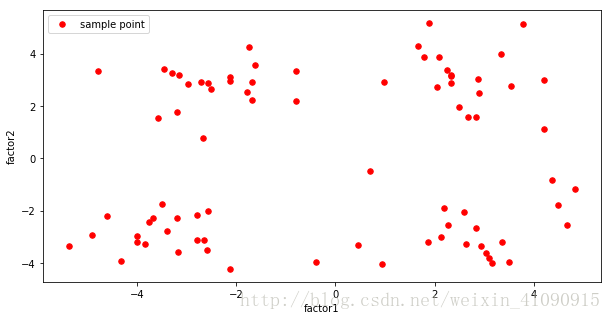
4）利用python的绘图库绘制样本点的散点图。其中横坐标为”factor1”，纵坐标为”factor2”。

point_x = data_set[:,0]
point_y = data_set[:,1]        
fig, ax = plt.subplots(figsize=(10,5))
ax.scatter(point_x, point_y, s=30, c="r", marker="o", label="sample point")
ax.legend()
ax.set_xlabel("factor1")
ax.set_ylabel("factor2")

绘制出的散点图如下图所示：

5）接下来定义一个计算两个向量之间欧氏距离的函数dist_eclud，已知向量 X=(x1,x2...xn) X = ( x 1 , x 2 . . . x n ) 和 Y=(y1,y2...yn) Y = ( y 1 , y 2 . . . y n ) 之间的欧氏距离为
(x1−y1)2+(x2−y2)2+...+(xn−yn)2−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√ ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + . . . + ( x n − y n ) 2

def dist_eclud(vecA, vecB):
    vec_square = []
    for element in vecA - vecB:
        element = element ** 2
        vec_square.append(element)
    return sum(vec_square) ** 0.5

6）构建 k k 个随机质心。输入参数为数据集data_set和想要构建的质心个数k。随机质心必须要在整个数据集的边界之内。首先可以找到数据集每一维的最小和最大值。然后得到每一维的取值范围。用0到1之间的随机数和取值范围相乘，再用最小值加上该乘积，就可以得到在每一维取值范围内的随机数。

# 构建k个随机质心
def rand_cent(data_set, k):
    n = data_set.shape[1]    
    centroids = np.zeros((k, n))
    for j in range(n):
        min_j = float(min(data_set[:,j]))
        range_j = float(max(data_set[:,j])) - min_j
        centroids[:,j] = (min_j + range_j * np.random.rand(k, 1))[:,0]
    return centroids

7）算法的主函数，输入参数为数据集和簇的个数。
首先初始化样本点的簇分配矩阵，有80行2列，第一列为该样本点的簇分配索引，第二列为该样本点到该簇质心的欧氏距离。
当任意一个点的簇分配发生变化时，迭代执行以下操作：遍历每个样本点，计算样本点i到各个质心的距离，找到最小距离，将该质心所在簇编号分配给该样本点。遍历完所有样本点后，重新计算每个簇的质心。直到所有样本点的簇分配都不再发生变化时迭代停止。
最后返回质心和样本点的簇分配矩阵

def Kmeans(data_set, k):    
    m = data_set.shape[0]   
    cluster_assment = np.zeros((m, 2))  
    centroids = rand_cent(data_set, k)  
    cluster_changed = True        
    while cluster_changed:       
        cluster_changed = False   
        for i in range(m):        
            min_dist = np.inf; min_index = -1   
            for j in range(k):     
                dist_ji = dist_eclud(centroids[j,:], data_set[i,:])
                if dist_ji < min_dist:              
                    min_dist = dist_ji; min_index = j   
            if cluster_assment[i,0] != min_index:    
                cluster_changed = True      
            cluster_assment[i,:] = min_index, min_dist**2   
        for cent in range(k):   
            pts_inclust = data_set[np.nonzero(list(map(lambda x:x==cent, cluster_assment[:,0])))]
            centroids[cent,:] = np.mean(pts_inclust, axis=0)
    return centroids, cluster_assment            

8）调用函数Kmean，输入数据集为data_set，簇数量为4个，得到收敛后的质心和簇分配矩阵(簇分配矩阵略)。

my_centroids, my_cluster_assment = Kmeans(data_set, 4)
print(my_centroids)
# print(my_cluster_assment)

得到的4个质心为：

9）为了更加清晰直观，用绘图库绘制散点图，其中，四个质心用黑色▲标出。

point_x = data_set[:,0]
point_y = data_set[:,1]  
cent_x = my_centroids[:,0]
cent_y = my_centroids[:,1]
fig, ax = plt.subplots(figsize=(10,5))
ax.scatter(point_x, point_y, s=30, c="r", marker="o", label="sample point")
ax.scatter(cent_x, cent_y, s=100, c="black", marker="v", label="centroids")
ax.legend()
ax.set_xlabel("factor1")
ax.set_ylabel("factor2")

得到的散点图如下图所示：

二、二分K-均值聚类

上述算法的聚类簇的数目 k k 是用户自定义的，那么用户如何才能知道 k k 的选择是否正确？如何才能知道生成的簇比较好呢？在包含簇分配结果的矩阵中保存着每个点的误差，即该点到簇质心的距离平方值。

一种用于度量聚类效果的指标使SSE(Sum of Squared Error，误差平方和)，SSE值越小表示数据点越接近它们的质心，聚类效果也就越好。

于是就可以采用二分K-聚类的方法，具体代码实现如下：

1）定义一个bi_Kmeans函数，两个输入参数分别为数据集和聚类簇数量。

该函数首先创建一个矩阵cluster_assment来存储数据集中每个点的簇分配结果及平方误差，然后计算整个数据集的质心，并使用一个列表cent_list来保留所有的质心。得到上述质心之后，可以遍历数据集中所有点来计算每个点到质心的误差值。这些误差值将会在后面用到。

接下来程序进入while循环，该循环会不停对簇进行划分，直到得到想要的簇数目为止。可以通过考察簇列表中的值来获得当前簇的数目。然后遍历所有簇来决定最佳的簇进行划分。

为此需要比较划分前后的SSE。一开始将最小SSE设置为无穷大，然后遍历簇列表cent_list中的每一个簇。对每个簇，将该簇中的所有点堪称一个小的数据集pts_incurr_cluster。将pts_incurr_cluster输入到函数Kmeans()中进行处理(k=2)。K-均值算法会生成两个质心(簇)，同时给出每个簇的误差值。这些误差与剩余数据集的误差之和作为本次划分的误差。如果该划分的SSE值最小，则保存本次划分。

一旦决定了要划分的簇，接下来就可以实际执行划分操作。划分操作很容易，只需要将划分的簇中所有点的簇分配结果进行修改即可。当使用Kmeans()函数并且制定簇数目为2时，会得到两个编号分别为0和1的结果簇。需要将这些簇编号修改为被划分簇以及新加簇的编号，该过程可以通过两个数组过滤器来完成。

最后，新的簇分配结果被更新，新的质心会被添加到cent_list中。

当while循环结束时，同Kmeans()函数一样，函数返回之心列表与簇分配结果。

# 二分K均值聚类的主函数，输入参数为数据集和要分的簇的个数
def bi_Kmeans(data_set, k):   
    m = data_set.shape[0]   # 得到data_set的行数，即数据集的个数
    cluster_assment = np.zeros((m,2)) # 初始化样本点的簇分配矩阵，第一列为簇分配索引，第二列为欧氏距离平方
    centroid0 = np.mean(data_set, axis=0)  # 按列计算均值，即找到初始质心
    cent_list = [centroid0]
    for j in range(m):   # 对于每个样本点
        cluster_assment[j,1] = dist_eclud(centroid0, data_set[j,:])**2 # 计算该样本点的误差平方
    while (len(cent_list) < k):   # 当已有的簇个数小于k时，迭代执行以下代码
        lowestSSE = np.inf     # 初始化误差平方和SSE的最小值

        # 找到对哪个簇进行划分可以最大程度降低SSE值
        for i in range(len(cent_list)):   # 遍历每个已有的簇
            # 得到属于该簇的所有样本点
            pts_incurr_cluster = \
            data_set[np.nonzero(list(map(lambda x:x==i, cluster_assment[:,0])))]
            # 将该簇的所有样本点通过函数Kmean进行划分(k=2),得到划分后的质心和簇分配矩阵
            centroid_mat, split_clust_ass = Kmeans(pts_incurr_cluster, 2)    
            sse_split = np.sum(split_clust_ass[:,1])  # 得到划分后的误差平方和
            # 得到其他样本点的误差平方和
            sse_not_split = \
            np.sum(cluster_assment[np.nonzero(list(map(lambda x:x!=i, cluster_assment[:,0]))),1])
            if (sse_split + sse_not_split) < lowestSSE:  # 如果总的误差平方和小于lowestSSE
                best_cent_to_split = i                   # 则保存本次划分
                best_new_cents = centroid_mat
                best_clust_ass = split_clust_ass
                lowestSSE = sse_split + sse_not_split
        # 对最大程度降低SSE值的簇进行划分

        # 将划分后得到的编号为0的结果簇的编号修改为原最大簇编号+1，即len(cent_list)
        best_clust_ass[np.nonzero(list(map(lambda x:x==1, best_clust_ass[:,0]))), 0] = len(cent_list)  
         # 将划分后得到的编号为1的结果簇的编号修改为被划分的簇的编号
        best_clust_ass[np.nonzero(list(map(lambda x:x==0, best_clust_ass[:,0]))), 0] = best_cent_to_split 
        cent_list[best_cent_to_split] = best_new_cents[0,:] # 更新被划分的簇的质心
        cent_list.append(best_new_cents[1,:])  # 添加一个新的簇的质心
        cluster_assment[np.nonzero(list(map(lambda x:x==best_cent_to_split, cluster_assment[:,0]))),:] = \
            best_clust_ass  # 将簇分配矩阵中属于被划分的簇的样本点的簇分配进行更新
    return np.array(cent_list), cluster_assment

2）接下来调用bi_Kmeans()函数，得到三个质心和簇分配结果(簇分配结果略)，在调用bi_Kmeans()函数前，先执行load_dataset()函数载入数据。

data_set2 = load_dataset(r"D:\python_data\MachineLearningInaction\machinelearninginaction\Ch10\testSet2.txt")

cent_list, cluster_assment = bi_Kmeans(data_set2, 3)
print(cent_list)

3）最后，用绘图库绘制散点图，横坐标为”factor1”，纵坐标为”factor2”，其中三个质心用黑色X标出。

point_x = data_set2[:,0]
point_y = data_set2[:,1] 
cent_x = cent_list[:,0]
cent_y = cent_list[:,1]
fig, ax = plt.subplots(figsize=(10,5))
ax.scatter(point_x, point_y, s=30, c="r", marker="o", label="sample point")
ax.scatter(cent_x, cent_y, s=100, c="black", marker="x", label="centroids")
ax.legend()
ax.set_xlabel("factor1")
ax.set_ylabel("factor2")

所绘制的散点图如下：